§7. Дифференциальное уравнение затухающих колебаний (механических и электромагнитных) и его решение

Свободными затухающими колебаниями называются колебания, амплитуда которых из-за потерь энергии колебательной системой с течением времени уменьшается.

Линейные системы - это идеализированные реальные системы, в которых параметры, определяющие физические свойства системы, в ходе процесса не изменяются.

Линейными системами являются: пружинный маятник при малых растяжениях ( когда справедлив закон Гука ), колебательный контур ( у которого индуктивность, емкость и сопротивление не зависят ни от тока в контуре, ни от напряжения ).

Различные по своей природе линейные системы описываются идентичными линейными дифференциальными уравнениями.

Дифференциальное уравнение затухающих колебаний линейной системы имеет вид:

,

(7.1)

где S - колеблющаяся величина , описывающая тот или иной физический процесс ;

 = const - коэффициент затухания;

_о - циклическая частота свободных незатухающих колебаний той же колебательной системы, т.е. при  = 0 ; _о - называется собственной частотой колебательной системы.

Рассмотрим решение уравнения (7.1) в виде:

,

(7.2)

где U = U ( t ), найдем и .

	,	(7.3)
	.	(7.4)

Подставив (7.3) и (7.4) в (7.1) получим:

.

(7.5)

Решение уравнения (7.5) зависит от знака коэффициента перед искомой величиной. Рассмотрим случай, когда этот коэффициент положителен

;

;

,

(7.6)

то имеем

.

(7.7)

Решением уравнения (7.7) является функция: U = A_o cos ( t +  )

Тогда решением уравнения (7.1) является функция

,

(7.8)

если затухание мало, (²  ²_о) то

,

(7.9)

амплитуда затухающих колебаний, А_о - начальная амплитуда.

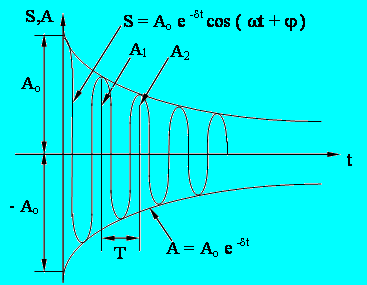
Рис.7.1. График зависимости амплитуды затухающих колебаний как функция от времени

Промежуток времени, в течении которого амплитуда затухающих колебаний уменьшается в е раз называется временем релаксации.

,

(7.10)

А = А_о e ^-t , А_о/A=e; ^- =1 => 1/ = 

Затухающие колебания не являются строго периодическими, и понятие периода можно вводить только при малых затуханиях, как промежуток времени между двумя последующими максимумами или минимумами колеблющейся физической величины.

С учетом этого:

.

(7.11)

Логарифмическим декрементом затухания () называется физическая величина числено равная логарифму натуральному отношению двух амплитуд, следующих друг за другом через период:

.

(7.12)

 / N_e = T.

В СИ [  ] = 1 - безразмерная величина, тогда из формулы связи :

.

(7.13)

[ Т ] = 1 с ,

[  ] = 1 / с = 1 с^-1

 - постоянная для данной колебательной системы величина.

N_e - число колебаний, совершаемых за время уменьшения амплитуды в е раз.

Для характеристики колебательной системы вводят понятие добротности Q, которая при  << 0, равна:

.

(7.14)

[Q] = 1 – величина безразмерная

(так как ² << _о², T = T₀)

Добротность, это физическая величина, обратно пропорциональная логарифмическому декременту затухания.

Учтем, что  = Т = (1/)*(Т/1) = 1 / N_e, тогда Q =  /  = N_e =  / Т_о = _о / 2

Выводы, полученные для свободных затухающих колебаний линейных систем, применимы для колебаний различной физической природы (механических, электромагнитных)
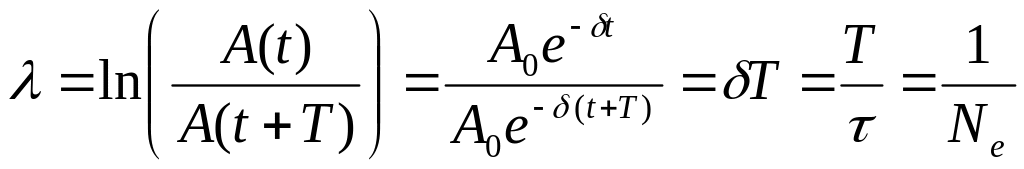