§3. Энергия механических гармонических колебаний

Пусть материальная точка совершает прямолинейные гармонические колебания вдоль оси координат х около положения равновесия, принятого за начало координат.

Тогда

.

(3.1)

По определению

	,	(3.2)
	.	(3.3)

А по второму закону Ньютона:

F = ma , и F_max= ma_max, тогда с учетом (3.3) получаем:

.

(3.4)

Сила пропорциональна смещению материальной точки из положения равновесия и направлена в противоположную сторону (к положению равновесия ).

.

(3.5)

Запишем выражения для кинетической, потенциальной и полной энергии материальной точки.

По определению

.

(3.6)

Т.к. , то

.

(3.7)

Но W = W_к + W_p , тогда

,

(3.8)

т. к. m = const, _о = const, A = const, то следует вывод:

Вывод: Полная энергия остаётся постоянной, так как при гармоническом колебании справедлив закон сохранении механической энергии и упругая сила консервативна.

§4. Гармонический осциллятор. Колебания пружинного, физического и математического маятников

Система, совершающая колебания, описываемые уравнением вида:

(4.1)

называется гармоническим осциллятором.

Колебания гармонического осциллятора являются важным примером периодического движения и служат точкой или приближенной моделью во многих задачах классической и квантовой физики.

Примером гармонического осциллятора являются: пружинный, физический, математический маятники, колебательный контур (для токов и напряжений столь малых, что элементы контура можно считать линейными).

1. Колебания пружинного маятника

Пружинный маятник – груз массой m, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы : F = – kx, где k – жесткость пружины, х – смещение груза от положения равновесия.

Получим дифференциальное уравнение гармонического колебания пружинного маятника:

и

F = – kx ,

тогда

		(4.2)
		(4.2)

Сравнив (4.2’) и (4.1)

,

(4.3)

тогда

,

(4.4)

отсюда, учитывая, что _о=2/Т, получим:

(4.5)

период колебаний пружинного маятника.

Формула (4.5) выполняется для упругих колебаний, когда справедлив закон Гука, т.е. когда m_пр  m_тела.

(4.6)

потенциальная энергия пружинного маятника.

F_упр=-dW_p/dx;

-W_p= -kxdx => W_p=kx²/2

F_т.упр консервативная сила, тогда

dA = - dW_p;

.

2. Колебания математического маятника

Идеализированная система, состоящая из математической точки массы m подвешенной на нерастяжимой невесомой нити и колеблющаяся под действием силы тяжести.

Пример: небольшой тяжелый шарик, подвешенный на тонкой длинной нити.

, гдеN - сила реакции нити на натяжении.

угол  - мал.

х - путь, пройденный шариком.

х = l  или  = х / l ; тогда F_в = - mgx / l

Но _о = , а F_упр = – kx , тогда mgx / l = kx  k = mg / l

		(4.6)
	,	(4.7)

( 4.7) дифференциальное уравнение ГК математического маятника.

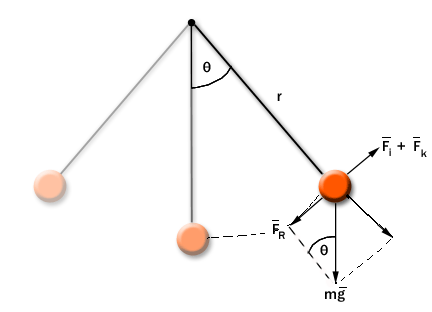
Рис. 4.1. Колебания математического маятника