
- •В.Н. Витвицкая, л.В. Климович линейная алгебра
- •Аналитическая геометрия
- •1. Матрицы и действия над ними
- •2. Определители и их вычисление
- •3. Обратная матрица. Ранг матрицы
- •4. Системы линейных уравнений и методы их решения
- •5. Векторная алгебра
- •6. Аналитическая геометрия
- •7. Полярная система координат. Построениие линии в полярной системе координат
- •8. Комплексные числа
- •9. Вопросы и задания при самостоятельной подготовке к экзамену
- •9.1. Элементы линейной алгебры
- •9.2. Векторная алгебра
- •9.3. Аналитическая геометрия
- •9.4. Комплексные числа
8. Комплексные числа
На множестве действительных чисел не всякое уравнение выше первой степени имеет решение. Так, например, уравнение х2 + 1 = 0 не имеет действительных корней. Это привело к расширению множества действительных чисел путём ввода чисел новой природы.
Число, удовлетворяющее равенству х2 = –1, обозначают символом i, его называют мнимой единицей. Таким образом, i2 = –1.
Число z = х + iy, где х и у - любые действительные числа; i – мнимая единица, называется комплексным числом. Числа х и у называются, соответственно, действительной и мнимой частью комплексного числа z и обозначаются x = Re z и y = Im z.
При х = 0 комплексное число х + iy обращается в чисто мнимое число iy ; при у = 0 получим число х + 0i, то есть действительное число х. Таким образом, множество комплексных чисел включает в себя и все действительные числа.
Комплексные числа вида х + iy и х – iy называются сопряжёнными. Комплексные числа х + iy и – х – iy называются противоположными.
Два комплексных числа х1 + iy1 и х2 + iy2 считаются равными тогда и только тогда, когда х1 = х2 и y1 = y2.
Известно, что действительные числа можно изображать на прямой. Комплексные числа z = х + iу взаимно однозначно сопоставляются с парами действительных чисел (х; у). Поэтому комплексное число z = х + iy условились геометрически изображать точкой M, у которой в прямоугольной системе координат абсцисса равна x, а ордината y (рис 8.1).
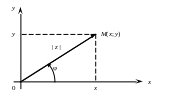
Рис. 8.1
Комплексное число
можно также изображать вектором с
началом в нулевой точке и концом в точке
M
(![]() ).
Длина вектора
называется
модулем
этого комплексного числа и является
неотрицательным числом. Обозначают его
символом |z|.
На чертеже (рис. 8.1) видно, что
).
Длина вектора
называется
модулем
этого комплексного числа и является
неотрицательным числом. Обозначают его
символом |z|.
На чертеже (рис. 8.1) видно, что
![]() .
.
Величина угла
вектора
![]() с положительным направлением оси абсцисс
называется
аргументом
комплексного
числа z
и обозначается Arg z
или φ.
Он связан с x
и y
следующими формулами:
с положительным направлением оси абсцисс
называется
аргументом
комплексного
числа z
и обозначается Arg z
или φ.
Он связан с x
и y
следующими формулами:
![]() или
или
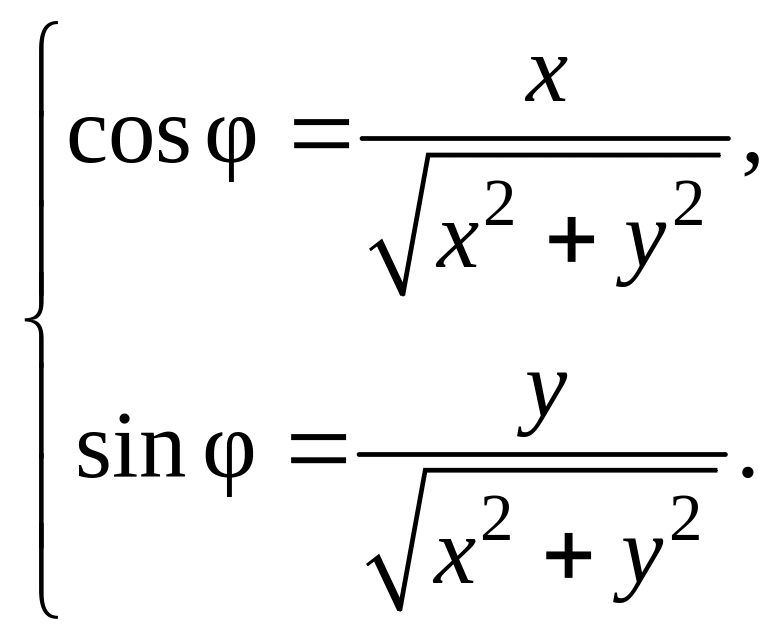
Форма записи комплексного числа z = х + iy называется алгебраической. Абсцисса х и ордината у комплексного числа z = x + iy выражаются через модуль |z| и аргумент φ (рис. 8.1) формулами:
![]() ,
y = |z|·sinφ,
,
y = |z|·sinφ,
Тогда получаем z = |z|·(cosφ + i·sinφ). Последнее выражение называется тригонометрической формой комплексного числа.
Для записи комплексных чисел также используют показательную форму:
z =|z|·eiφ,
где |z|–модуль, а φ– аргумент комплексного числа.
Пример 1. Представить в тригонометрической форме число z = – 3 + 2i.
Решение. Так как , a , то в нашем случае имеем
![]()
Тангенс отрицателен,
следовательно, значение φ
надо искать
во второй или четвёртой четвертях.
Обращаясь к формулам для sin φ
и cos φ,
замечаем,
что при х =
–3 и у = 2
синус
положителен, а косинус отрицателен, что
имеет место во второй четверти (удобнее
четверть определять по знакам при x
и у).
В данном
случае находим φ = 146°18´,
значит
![]() .
.
Пример 2. Представить в тригонометрической форме число z = 1 – i.
Решение. Имеем
![]() .
Здесь x = 1,
y = –1.
Следовательно, угол φ находится в
четвёртой четверти. Отсюда рассчитываем
φ = 7π/4
и можем записать
.
Здесь x = 1,
y = –1.
Следовательно, угол φ находится в
четвёртой четверти. Отсюда рассчитываем
φ = 7π/4
и можем записать
![]() .
.
Пример 3.
Выразить в
алгебраической форме число
![]() .
.
Решение. Так
как
![]() ,
то комплексное число в алгебраической
форме принимает вид:
,
то комплексное число в алгебраической
форме принимает вид:
![]() .
.
Над комплексными числами производятся те же действия, что и над действительными.
Суммой комплексных чисел х1 + i y1 и х2 + i y2 называется комплексное число (х1 + х2) + (y2 + y2) i.
Произведением комплексных чисел х1 + y1 i и х2 + y2 i называется комплексное число (х1 х2 - y1 y2) + (х1 y2 + y1 х2) i.
Пример 4. Найти сумму и произведение комплексных чисел z1 = 2 – 3i и z2 = –1 + 2i
Решение.
z1+z2= 2 – 3i + (–1 + 2i) = (2–1) + (–3+2)·i = 1– i.
z1·z2== (2 – 3i) · (–1 + 2i) = 2·(–1) + 2·2i + (–3i)·(–1) + (–3i)·2i = = –2 + 4i +3i –6i2.
Деление комплексных чисел проводят следующим образом: сначала умножают числитель и знаменатель на число, сопряжённое знаменателю, после чего знаменатель станет действительным числом, а затем проводят деление действительной и мнимой частей отдельно.
Пример 5. Найти частное от деления комплексных чисел –2+ 5i и –3–4i.
Решение. Умножаем числитель и знаменатель на число, сопряжённое знаменателю, то есть на –3+4i:
![]() .
.
Использование показательной формы комплексных чисел во многих случаях значительно упрощает вычисления.
Пример 6. Найти произведение частное от деления комплексных чисел z1 = 3 · z2
z1 z2
Возведение комплексного числа в целую степень производится формуле Муавра:
zn = | z |n·einφ, если число задано в показательной форме;
или, в тригонометрической форме,
zn = | z |n·( cos nφ + i·sin nφ ),
где n - натуральное число.
Извлечение корня п-ой степени из комплексного числа z = |z|(cos φ + i sin φ) осуществляют с помощью формулы
![]() (8.1)
(8.1)
Здесь ______ – арифметический, а k = 0, 1,2 ... n-1.
Корень степени n в множестве комплексных чисел имеет п различных значений (но при z = 0 все значения корня равны между собой и равны нулю).
Пример 5.
Пример 7. Найти кубический корень из единицы.
Решение. Запишем
тригонометрическую форму единицы:
1 = l·(cos 360°k + i·sin 360°k).
Тогда
![]() = l·(cos
120°k
+ i·sin
120°k).
При k= 0,
1, 2 получим, соответственно:
= l·(cos
120°k
+ i·sin
120°k).
При k= 0,
1, 2 получим, соответственно:
z1 = 1·( cos 0° + i·sin 0° ) = 1;
z2 = 1·( cos 120° + i·sin 120° ) =
z3 = 1·( cos 240° + i·sin 240° ) =
Пример 8.
Дано
комплексное число а
=![]() .
.
Требуется: 1) записать число а в алгебраической и тригонометрической формах; 2) найти все корни уравнения z3 + а= 0.
Решение. 1) Чтобы представить комплекское число а в алгебраической форме, умножим его числитель и знаменатель на число сопряжённое знаменателю:
![]()
Получим a = –1 + i – алгебраическая форма комплексного числа.
Тригонометрическая форма комплексного числа а имеет вид
2) Решим уравнение z3 + а = 0 или z3 = –a:
По формуле (8.1) получим
Данный пример может быть использован при решении номеров 91-100 контрольной работы 1.
