6. Аналитическая геометрия

Всякое уравнение первой степени

. (6.1)

относительно координат x, y, z определяет плоскость в пространстве.

Вектор , координатами которого являются коэффициенты при х, у, z в уравнении (6.1), перпендикулярен плоскости и называется её нормальным вектором.

Уравнение плоскости, проходящей через данную точку М₀ (х₀, у₀, z₀) перпендикулярно вектору , имеет вид

. (6.2)

Если плоскость проходит через три данных точки М₁ (х₁; у₁; z₁), М₂ (х₂;  у₂; z₂) и М₃ (х₃; у₃; z₃), то её уравнение имеет вид

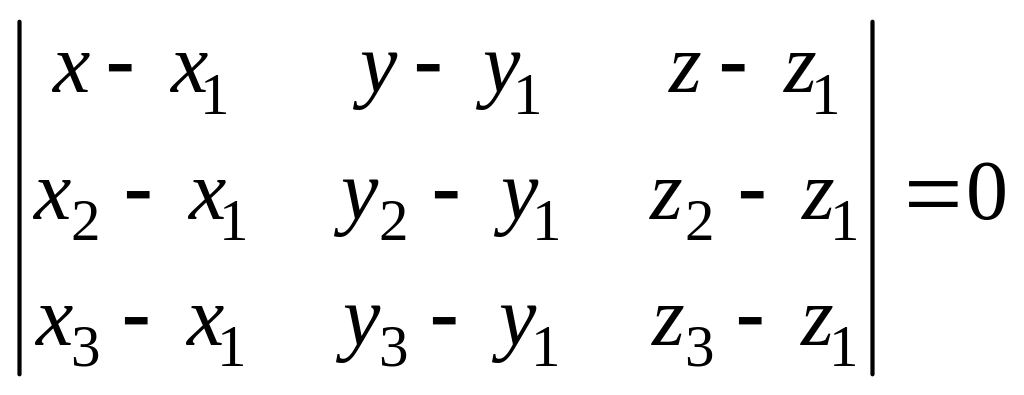. (6.3)

Прямую в пространстве можно определить как линию пересечения двух непараллельных плоскостей:

(6.4)

Каноническое уравнение прямой имеет вид

, (6.5)

где М₀ (х₀; у₀; z₀) - точка, лежащая на прямой, a - на-правляющий вектор прямой.

Если прямая проходит через две точки М₁ (х₁; у₁; z₁) и М₂ (х₂; у₂; z₂), то она определяется уравнениями

. (6.6)

В этом уравнении в качестве направляющего вектора выбран вектор .

Угол между прямой и плоскостью определяется по формуле:

. (6.7)

Пример 1. Даны координаты вершин пирамиды ABCD: А (2; 1;  0), B (3; –1; 2), С (13; 3; 10), D (0; l; 4).

Требуется: 1) записать векторы , , в базисе , найти модули этих векторов; 2) найти угол между векторами и ; 3) найти проекцию вектора на вектор ; 4) найти площадь грани ABC; 5) найти объем пирамиды ABCD.

Решение. 1) Произвольный вектор в системе орт определяют по формуле (5.2):

Если даны точки М₁ (х₁; у₁; z₁), М₂ (х₂; у₂; z₂), то координаты вектора находят по формулам

Вектор .

Аналогично найдем и .

По формуле (5.3) определяем длины этих векторов:

=3, =15, .

2) Скалярное произведение векторов и вычисляем по формуле (5.6)

.

Модули этих векторов уже найдены.

Следовательно, используя формулу (5.7), = 0,6, поэтому угол между векторами и φ = arcos 0,6 = 53°8'.

3) Проекцию вектора на вектор определяем по формуле (5.9):

.

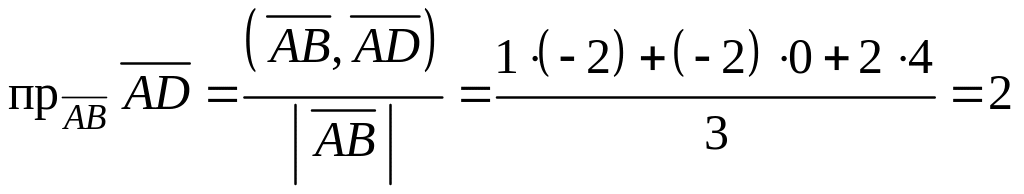4) Из геометрического смысла модуля векторного произведения следует, что площадь грани ABC равна половине площади параллелограмма, построенного на векторах и :

.

Найдём векторное произведение векторов и :

.

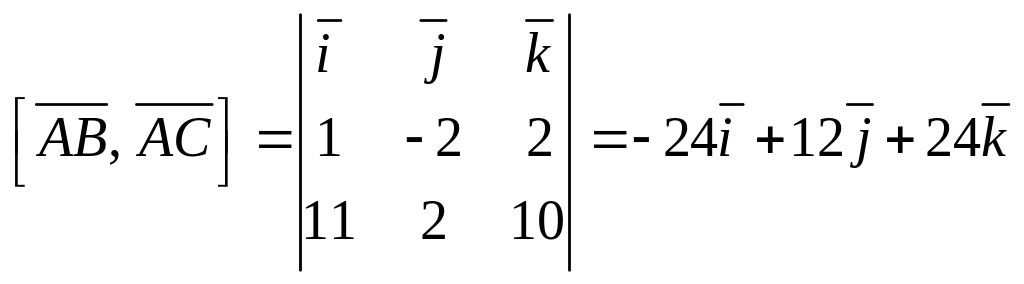Отсюда .

5) Объём параллелепипеда вычислим по формуле (5.13)

.

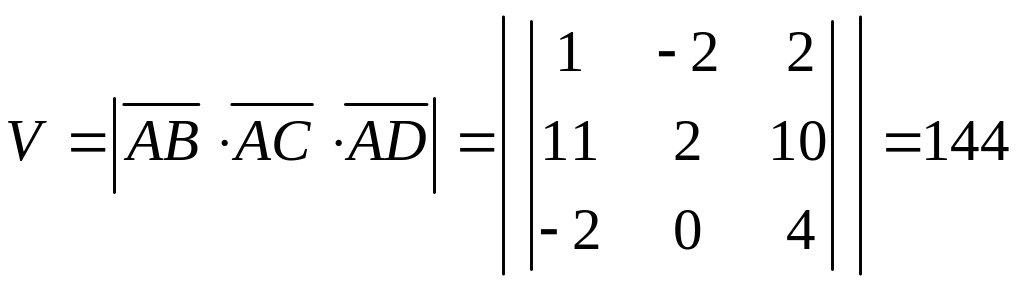Объём заданной пирамиды ABCD равен 1/6 объёма параллелепипеда, то есть равен 24.

Пример 2. Даны координаты четырёх точек: А (0; –2; –1), В (2; 4; –2), С (3; 2; 0), M (–11; 8; 10). Требуется: 1) составить уравнение плоскости, проходящей через точки A, В, С; 2) составить каноническое уравнение прямой, проходящей через точку М перпендикулярно плоскости ABC; 3) найти точку пересечения полученной прямой с плоскостью ABC и с координатными плоскостями хОу, xОz, yОz; 4) вычислить расстояние от точки М до плоскости ABC.

Решение. 1) Уравнение плоскости, проходящей через три данные точки, составляем по формуле (6.3), подставив в неё координаты точек A, В, С:

Разложим определитель по элементам первой строки:

10 x–5 (y + 2) – 10 (z + 1) = 0.

Сократив на 5, получим уравнение искомой плоскости ABC:

2 x – y – 2 z – 4 = 0

(общее уравнение плоскости ABC).

2) Подставив в уравнение (6.5) координаты точки М и заменив числа т,. п, p, соответственно, числами 2; –1; –2 (коэффициенты общего уравнения плоскости ABC), получим уравнение прямой, проходящей через точку М перпендикулярно плоскости ABC:

3) Запишем каноническое уравнение прямой в параметрическом виде. Пусть , где t – некоторый параметр.

Тогда параметрическое уравнение уравнение прямой можно записать в виде

x = 2t –11; y = –t +8; z = –2 t +10.

Подставив х, у, z в общее уравнение плоскости ABC, получим значение параметра t:

2(2t –11) –(–t +8) –2(–2 t +10) –4 = 0;

4 t –22 +t –8 +4 t –20 –4 = 0;

9 t –54 = 0; t = 6.

Находим координаты точки пересечения:

Точка пересечения, обозначим её Р, имеет координаты Р (1; 2; –2).

Пусть P₁ –точка пересечения прямой с координатной плоскостью хОу; уравнение этой плоскости z = 0. При z = 0 из параметрического уравнения прямой получаем

t = 5; x = –1; y = 3; P₁ (–1; 3; 0).

Пусть P₂ – точка пересечения этой же прямой с плоскостью xОz; уравнение этой плоскости у = 0. При у = 0 из параметрического уравнения имеем:

t = 8; x = 5; z =–6; P₂ (5; 0; –6).

Пусть P₃ – точка пересечения прямой с плоскостью yОz; уравнение этой плоскости х = 0. При х = 0 получим:

t = 5,5; y = 2,5; z = –1; P₃ (0; 5,5; –1 ).

4) Так как точка М лежит на прямой

,

которая перпендикулярна плоскости ABC и пересекается с ней в точке Р, то для нахождения расстояния от точки до плоскости достаточно найти длину вектора по формуле (5.3)

Пример 3. Даны координаты вершин пирамиды А₁ (2; 0; 0), А₂ (0; 3; 0), А₃ (0; 0; 6), А₄ (2; 3; 8). Найти: 1) длину ребра А₁А₂; 2) угол между рёбрами А₁А₂ и А₁А₄; 3) площадь грани А₁А₂А₃; 4) объём пирамиды; 5) уравнение прямой А₁А₂; 6) уравнение плоскости А₁А₂А₃; 7) угол между ребром А₁А₄ и гранью А₁А₂А₃; 8) уравнение высоты, опущенной из вершины А₄ на грань А₁А₂А₃. Сделать чертёж.

Решение. Построим пирамиду А₁А₂А₃А₄ (рис. 6.1).

Рис. 6.1

1) Прежде чем найти длину ребра А₁А₂, определим координаты вектора (для этого из координат конца вектора вычитаем соответствующие координаты начала):

= (0–2; 3–0; 0–0) или (–2; 3; 0).

По формуле (5.3) длина ребра

2) Угол φ между рёбрами А₁А₂ и А₁А₄ можно найти как угол между векторами и по формуле (5.8).

Найдём координаты вектора =(2 – 2; 3 – 0; 8 – 0), или (0; 3; 8). Затем определим угол:

,

.

3) Площадь грани А₁А₂А₃ , то есть площадь треугольника, равна половине площади параллелограмма, построенного на векторах и . Площадь параллелограмма по формуле (5.10) будет равна:

.

Вычислим координаты вектора =(0 – 2; 0 – 0; 6 – 0) или =(–2; 0; 6).

Найдем векторное произведение

.

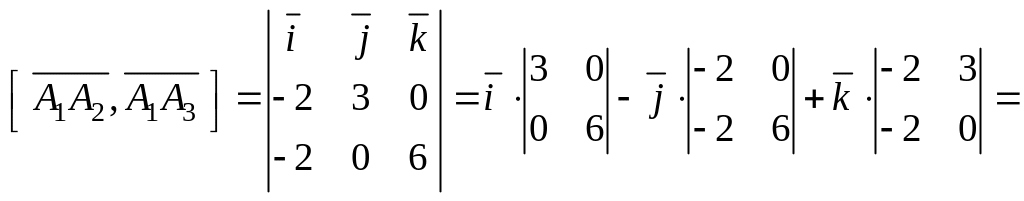
Отсюда

.

4) Объём пирамиды равен 1/6 объёма параллелепипеда, построенного на векторах , , . Объём параллелепипеда найдём по формуле (5.13)

.

Смешанное произведение найдём по формуле (5.12)

.

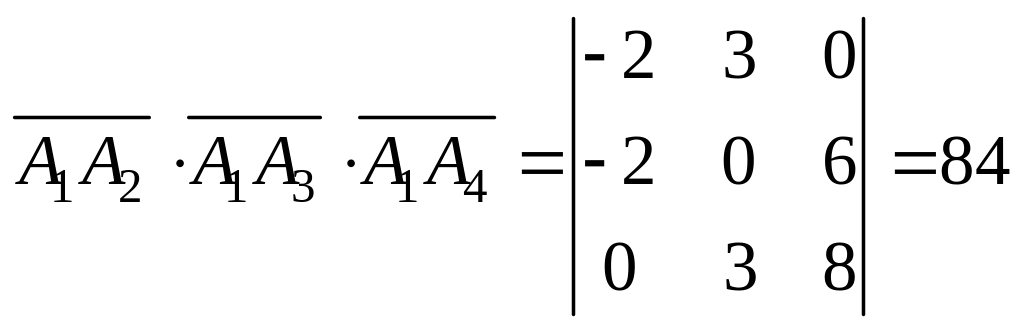Отсюда .

5) Для составления уравнения прямой А₁А₂ используем каноническое уравнение прямой (6.5), где х₀, у₀, z₀ – координаты точки А₁ (2; 0; 0); за направляющий вектор прямой возьмём вектор =(–2; 3; 0). Каноническое уравнение прямой примет вид

6) По формуле (6.3) составим уравнение грани А₁А₂А₃:

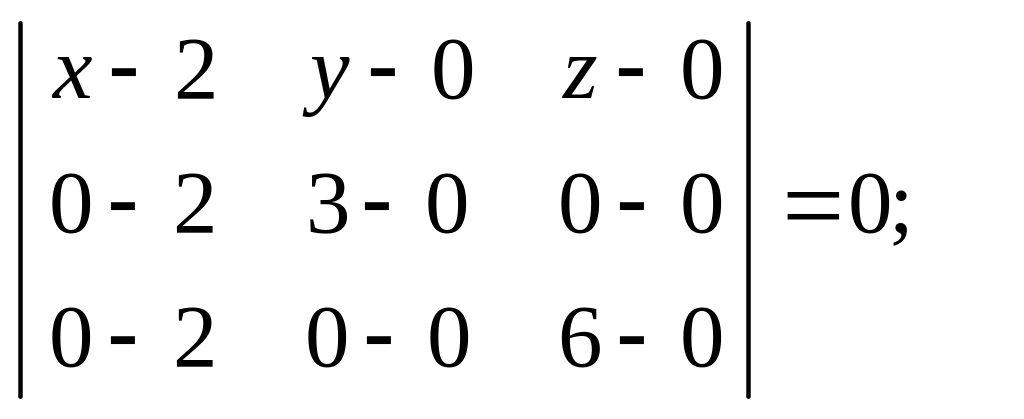
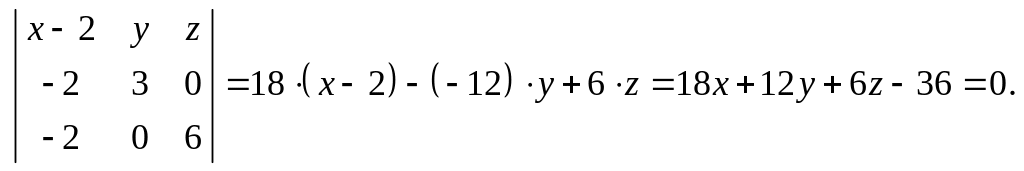
Сократив выражение на 6, получим уравнение грани А₁А₂А₃:

3x +2y +z –6 = 0.

7) Угол между прямой А₁А₄ и гранью А₁А₂А₃ определяется по формуле (6.7). Вектор (0; 3; 8) является направляющим для прямой А₁А₄, т.е. . Подставим в формулу (6.7) координаты направляющего вектора для прямой А₁А₄ и вектора нормали плоскости А₁А₂А₃ (3; 2; 1)

Тогда угол φ ≈ arcsin 0,44≈ 26,10°.

8) Нормальный вектор плоскости 3x +2y +z –6 = 0 (3; 2; 1) параллелен высоте, опущенной из А₄ на грань А₁А₂А₃. Его можно взять в качестве направляющего вектора для построения прямой. Составим каноническое уравнение высоты, подставив в уравнение (6.5) координаты точки A₄ и вектора :

Данный пример может быть использован для решения заданий 11–12 контрольной работы №1.