Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
«Сибирский федеральный университет»
Институт фундаментальной подготовки
В.Н. Витвицкая, л.В. Климович линейная алгебра
И
Аналитическая геометрия
Рекомендовано
редакционно-издательским советом
университета в качестве методических указаний к контрольной работе 1 для студентов заочной ускоренной формы обучения всех специальностей.
Красноярск 2007
УДК 512.64:514.12(072)
Линейная алгебра и аналитическая геометрия: Метод. указания к контрольной работе 1 для студентов заочной ускоренной формы обучения всех специальностей / В.Н. Витвицкая, Л.В. Климович С; ГОУ ВПО «Сибирский федеральный университет» ИФП. – Красноярск, 2009. –
Дано краткое изложение теоретического материала по линейной алгебре и аналитической геометрии
Рассмотрено подробное решение всех типовых задач, представленных в контрольной работе 1 для заочников первого курса ускоренной формы обучениия..
© Сибирский федеральный университет
Институт фундаментальной подготовки, 2009
© В.Н. Витвицкая,
Л.В. Климович
ВВЕДЕНИЕ
Цель настоящих методических указаний помочь студентам-заочникам ускоренной формы обучения освоить учебный материал и выполнить контрольную работу №1 по теме «Линейная алгебра и аналитическая геометрия».
Линейная алгебра является важным математическим аппаратом для решения широкого круга задач как теоретических (в математическом анализе, теории вероятностей, математической статистике, математическом программировании и т.д.), так и прикладных.
Рассмотрены темы: матрицы и определители, ранг матрицы, системы линейных уравнений.
В работе даны указания и разъяснения по вопросам: плоскость; прямая в пространстве; кривые второго порядка; полярная система координат; комплексные числа.
Каждая тема начинается с теоретического введения, где приводятся основные определения, формулы, свойства изучаемых объектов, иллюстрируемые примерами решения математических задач.
Среди приведенных задач имеются такие, которые можно назвать типовыми. Это особенно важно для студентов, занимающихся заочно.
В методических указаниях приведены вопросы и задания для самостоятельного контроля, которые помогут студентам успешно подготовиться к сдаче экзамена по рассмотренным темам.
1. Матрицы и действия над ними
Матрицей размерности m× n называется прямоугольная таблица чисел аij, расположенных в m строках и n столбцах:
А =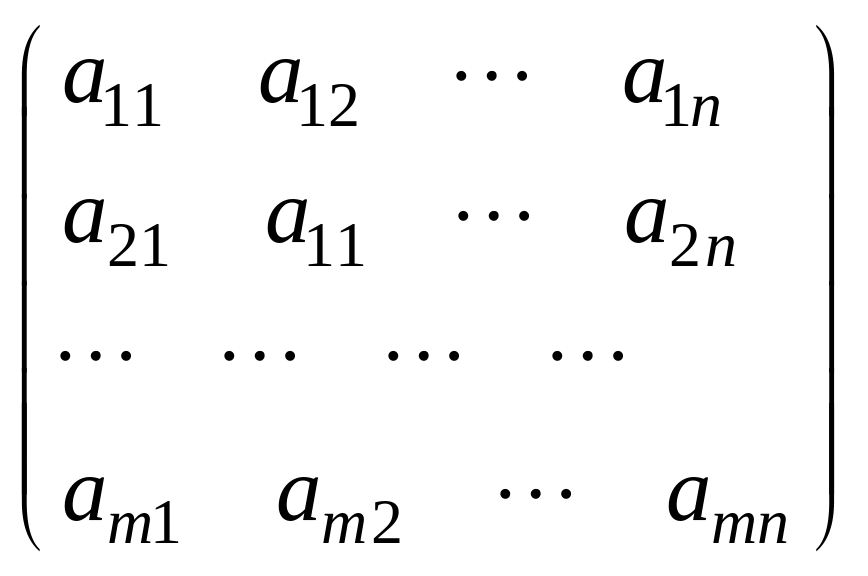
.
Будем обозначать матрицу большими буквам A, B, C, …, а ее элементы через аij, bij, cij, … .
Матрицу называют квадратной, если число строк m равно числу столбцов n. Ее элементы а11 , а22 , а33 , … , аnn образуют главную диагональ, а а1 n, а2 n-1, а3 n-2, …, аn1 – побочную диагональ.
Например, в матрице
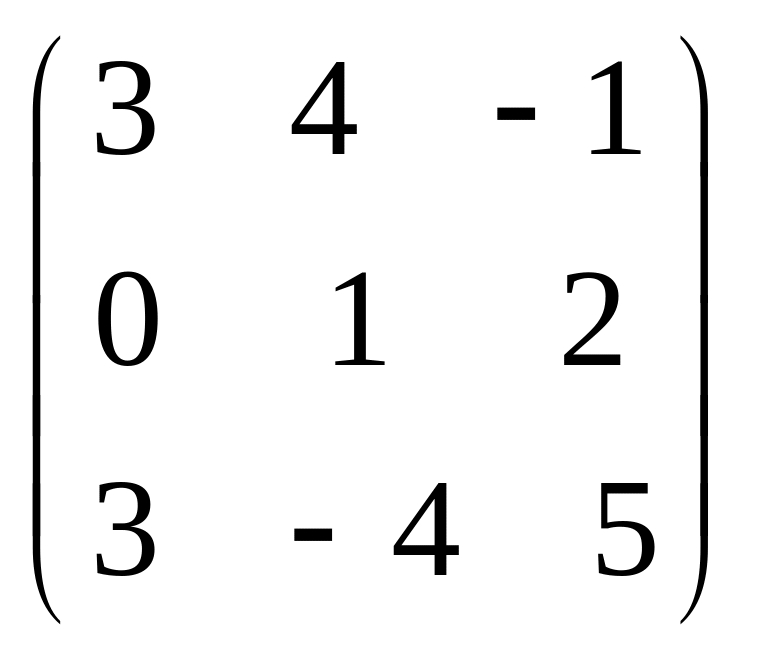элементы 3, 1, 5 образуют главную диагональ,
а элементы –1, 1, 3 – побочную.
Квадратная матрица называется диагональной, если ее элементы, не стоящие на главной диагонали, равны нулю. Диагональная матрица называется единичной, если элементы на главной диагонали равны единице.
Например,
–
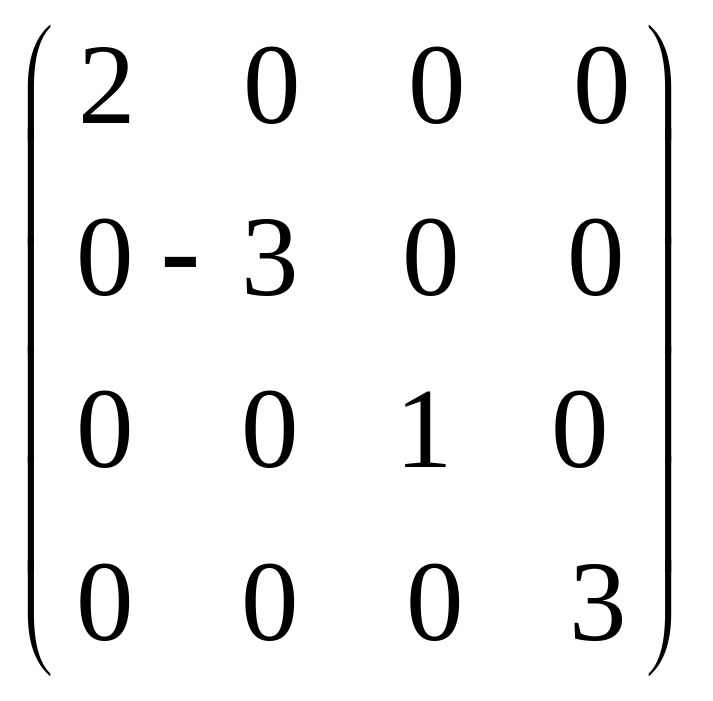диагональная матрица,
–
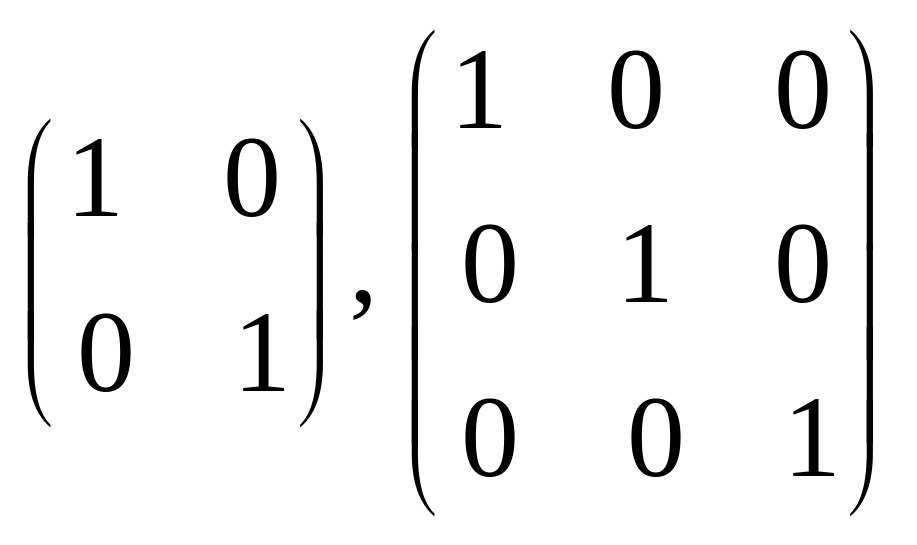единичные матрицы
второго и третьего порядков соответственно.
Квадратная матрица, у которой все элементы ниже или выше главной диагонали равны нулю, называется матрицей треугольного вида. Матрица произвольной размерности, у которой ненулевые элементы образуют «трапецию», называется трапециевидной.
Например,
,
–
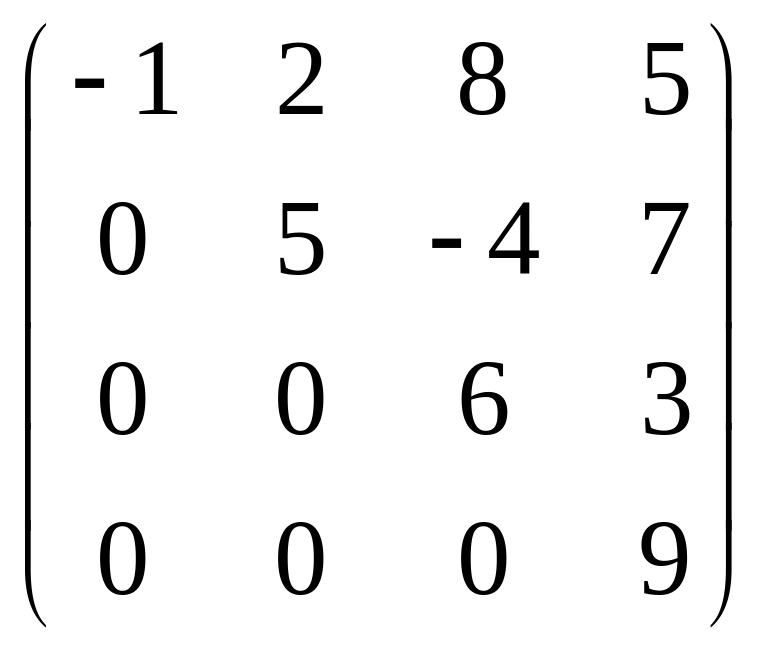треугольные матрицы,
–
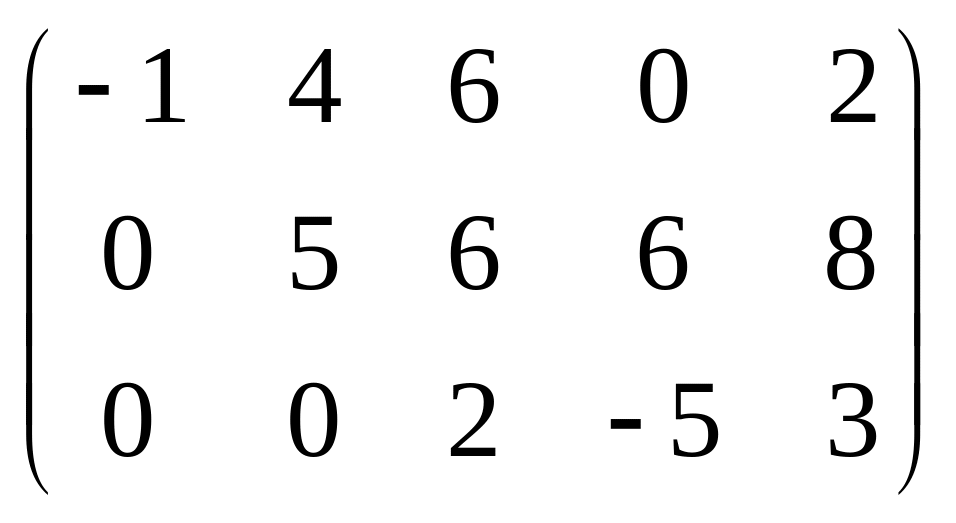трапециевидная
матрица.
К линейным операциям над матрицами относятся сложение (вычитание) матриц и умножение матрицы на число.
Суммой матриц A и B одинаковой размерности называется матрица C той же размерности, элементы которой равны суммам соответствующих элементов матриц А и В, например:
Произведением матрицы Am×n на число α называется матрица Bm×n, каждый элемент которой равен произведению числа α на соответствующий элемент матрицы А, например:
Произведением матрицы Am×n на матрицу Bn×k называется матрица Cm×k, каждый элемент cij которой равен сумме произведений элементов i-той строки матрицы А на соответствующие элементы j-того столбца матрицы В, (i = 1, 2,… , m; j = 1, 2, …, n):
cij = аi1 b1j + аi2 b2j + аin bnj.
Пример 1. Найти произведение матрицы А на матрицу В, если:
а) A3×1
=
,
B1×3
= (1 – 1 2);
б)
Решение: а) Проверим существование произведения матриц:
A3×1 · B1×3 = C3×3.
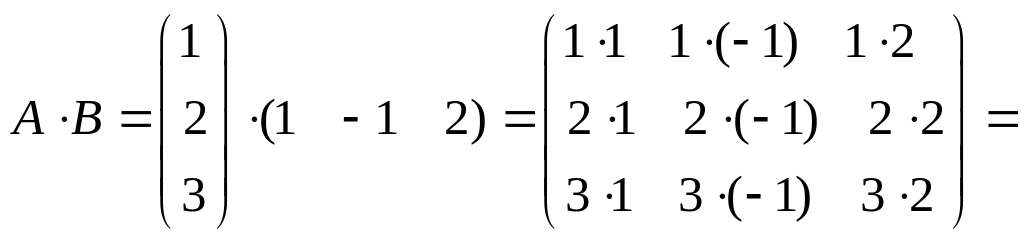
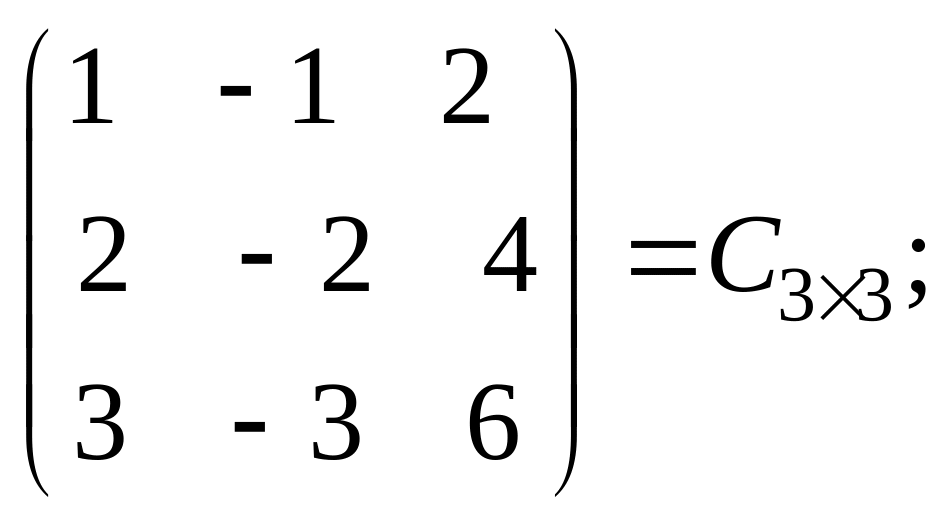
б)
Произведение матриц зависит от порядка множителей. В общем случае A·B ≠ B·A, даже если произведения A·B и B·A существуют.
Матрицей, транспонированной к данной, называется матрица АT, полученная из матрицы А заменой каждой ее строки на столбец с тем же номером.
Пример 2. Найти AT, если А:
а) А
=
;
б) А
=
.
Решение:
а) AT
= (4 –1 2);
б) AT
=
.