5. Векторная алгебра
Вектором называют направленный отрезок.
В векторной алгебре рассматриваются свободные векторы, то есть такие векторы, которые можно переносить в любую точку пространства, сохраняя длину и направление.
Векторы называются коллинеарными, если они параллельны или лежат на одной прямой.
Три вектора, параллельные или лежащие в одной плоскости, называются компланарными.
Упорядоченная
пара
и
неколлинеарных
векторов называется базисом
на плоскости.
Упорядоченная
тройка
,
,
некомпланарных
векторов называется базисом
в пространстве.
Любой вектор
в пространстве
может быть представлен в виде линейной
комбинации векторов
,
,
:
(5.1)
Запись (5.1) называется разложением вектора по базису , , , а числа α1, α2, α3 в этом разложении называются координатами вектора в данном базисе.
Если векторы
,
,
единичные и ортогональные (перпендикулярные)
между собой, то такой базис называется
прямоугольным, или декартовым. В этом
случае векторы
,
и
,
определяющие базис, называются,
соответственно, векторами-ортами
.
Свободный вектор
,
заданный в
координатном пространстве Oxyz,
может быть
разложен единственным образом по базису
:
,
(5.2)
где ах, ay, az - координаты вектора в этом базисе.
Длину (модуль) вектора вычисляют по формуле
(5.3)
Направление вектора определяется углами α, β, γ, образованными им с осями координат Ox, Oy и Oz. Косинусы этих углов (направляющие косинусы) рассчитывают по формулам:
,
,
.
(5.4).
При сложении векторов их соответствующие координаты складывают, а при умножении на число - умножают на это число.
Скалярным
произведением векторов
и
называется
число, равное произведению длин этих
векторов на косинус угла между ними:
.
(5.5)
Скалярное произведение также обозначают · .
Если векторы
и
заданы своими
координатами
,
,
их скалярное
произведение можно определить так:
.
(5.6)
Угол между векторами и ( ≠ 0, ≠ 0 ) определяется как
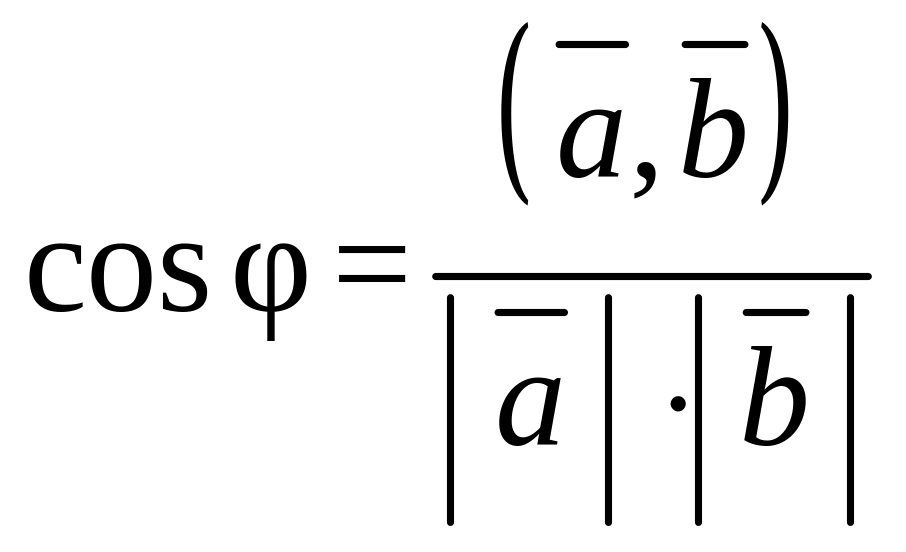(5.7)
В координатной форме формула (5.6) имеет вид
.
(5.8)
С геометрической точки зрения, скалярное произведение представляет собой произведение модуля вектора на проекцию вектора на вектор :
.
(5.9)
Векторным
произведением вектора
на вектор
называется
вектор
,
удовлетворяющий
условиям:
1)
;
2)
;
3) направление вектора таково, что векторы , , образуют правую тройку (т.е. поворот от вектора к вектору , наблюдаемый с конца вектора , происходит против часовой стрелки).
Обозначается
векторное произведение
или
×
.
Геометрический смысл модуля векторного произведения состоит в том, что он численно равен площади параллелограмма, построенного на перемножаемых векторах и как на сторонах:
.
(5.10)
Формула векторного произведения, если заданы координаты векторов, имеет вид
.
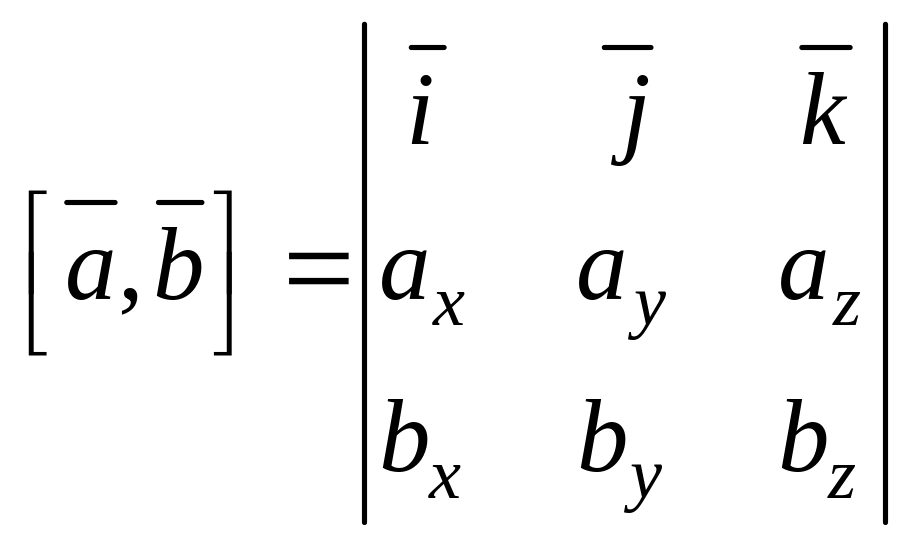(5.11)
Смешанным произведением векторов , , называется скалярно-векторное или векторно-скалярное произведение векторов, то есть
.
Смешанное произведение через координаты перемножаемых векторов представлено формулой
.
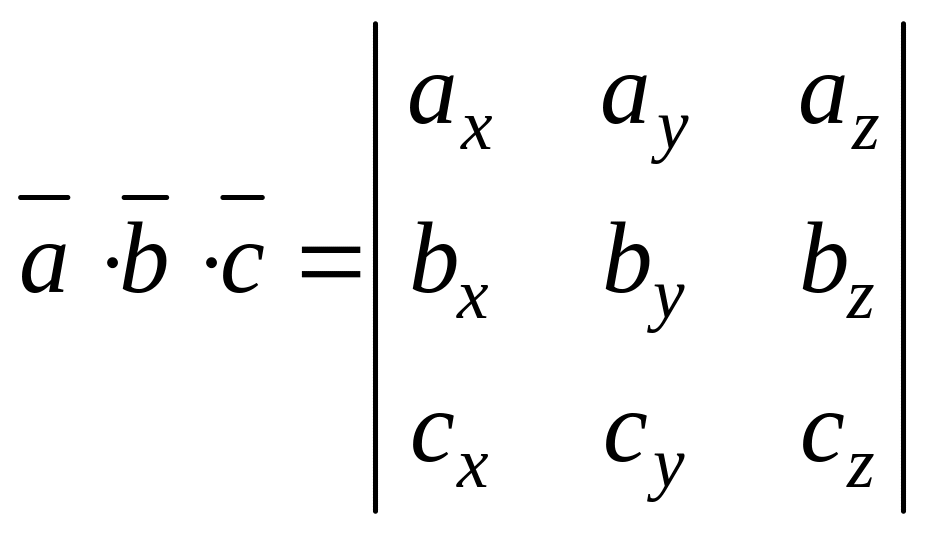(5.12)
Смешанное произведение трёх векторов , , по модулю равно объёму параллелепипеда, построенного на этих векторах:
.
(5.13)
Условия коллинеарности, перпендикулярности и компланарности векторов состоят в следующем:
1)
;
(5.14)
2)
;
(5.15)
3) векторы , , компланарны, если их смешанное произведение равно нулю:
.
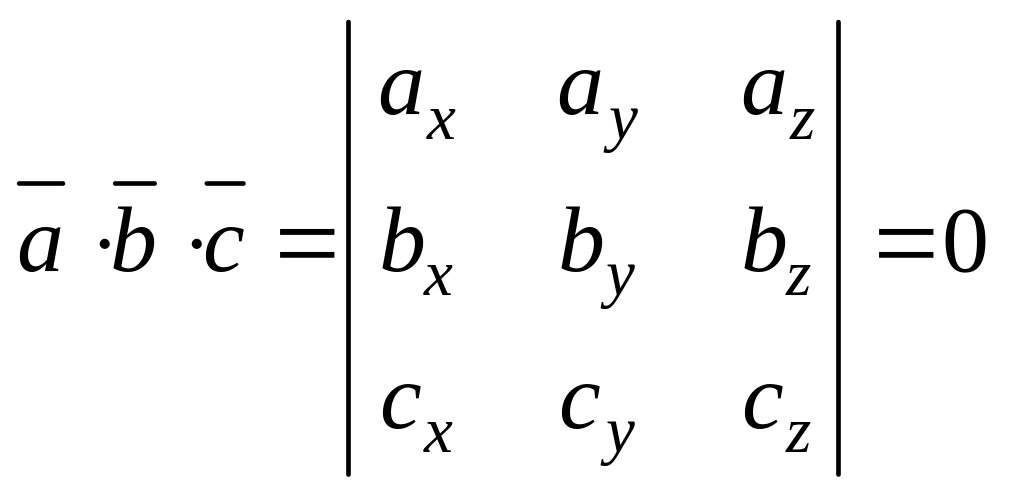(5.16)
Пример.
Даны векторы
=(2; 3; 1),
=(–1; 2; –2),
=(1; 2; 1),
и
=(2; –2; 1)
в некотором базисе. Показать, что векторы
,
,
образуют
базис, и найти координаты вектора
в этом базисе.
Решение. Базис во множестве всех векторов пространства могут составить любые три некомпланарных вектора. Если векторы некомпланарны, то их смешанное произведение не равно нулю. Покажем, что векторы , , не компланарны. Найдем их смешанное произведение:
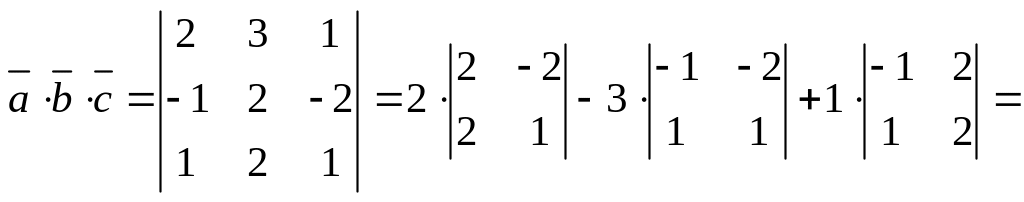
= 2∙6 – 3∙1 + 1∙(–4) = 5 ≠ 0.
Векторы , , не компланарны, следовательно, образуют базис.
Разложим вектор по базису , , :
.
Для нахождения координат вектора (α1; α2; α3) в базисе , , составим следующую систему уравнений:
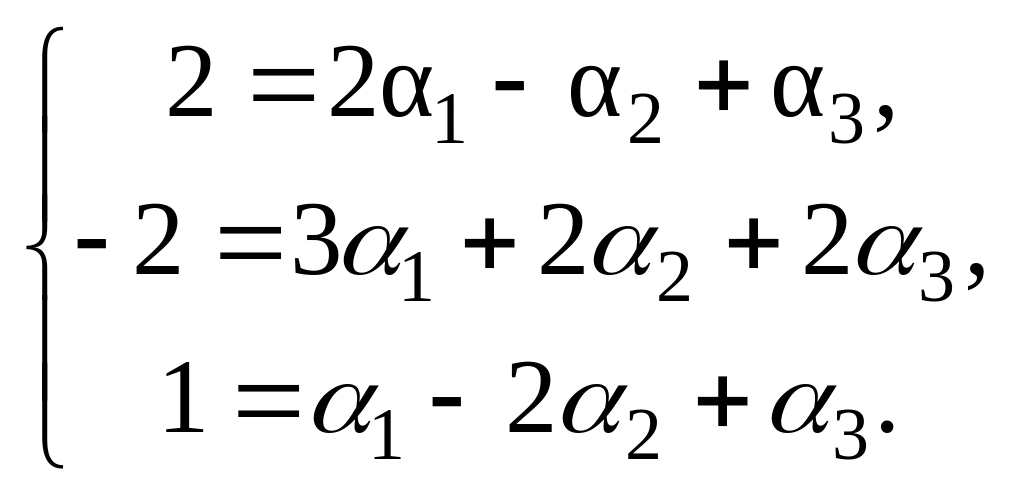
По формулам Крамера найдём α1, α2, α3:
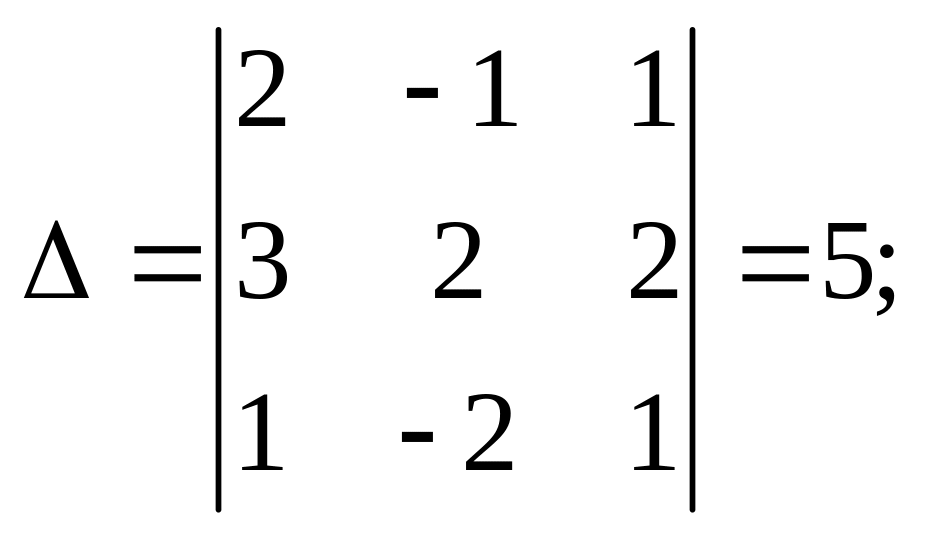
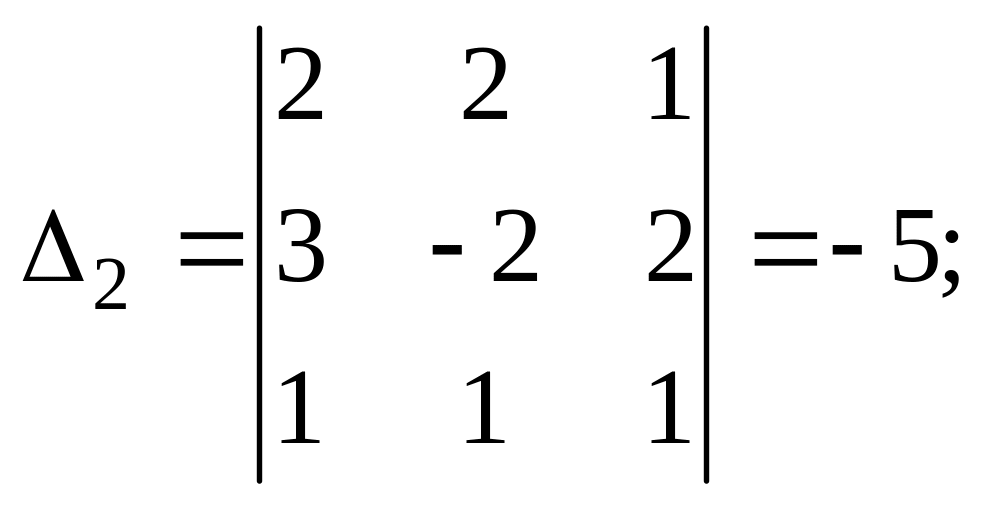
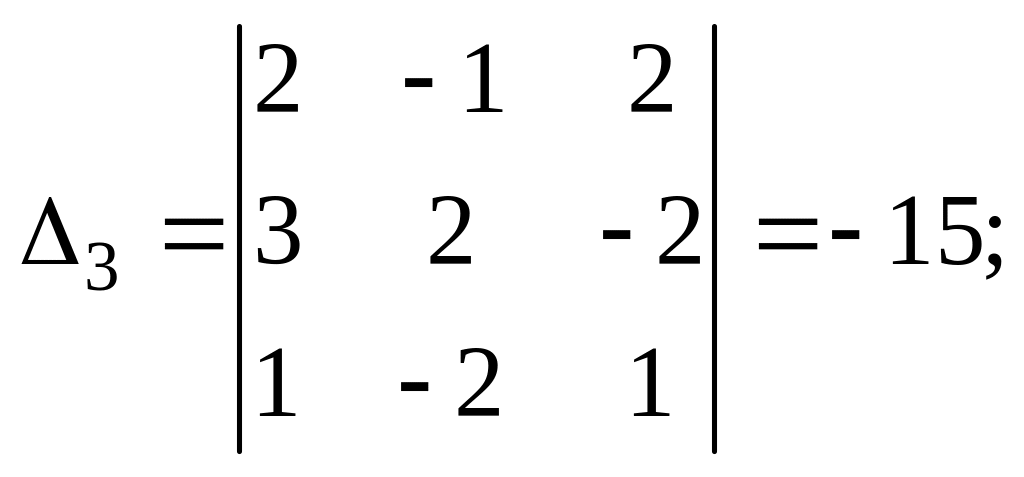
Решение системы образует совокупность координат вектора в базисе , , :
или
.
Разобранный выше пример применим в качестве образца для решения номеров 1 – 10 контрольной работы № 1.