4. Системы линейных уравнений и методы их решения

Система m линейных уравнений с n неизвестными х₁, …, х_n называется линейной, если она имеет вид:

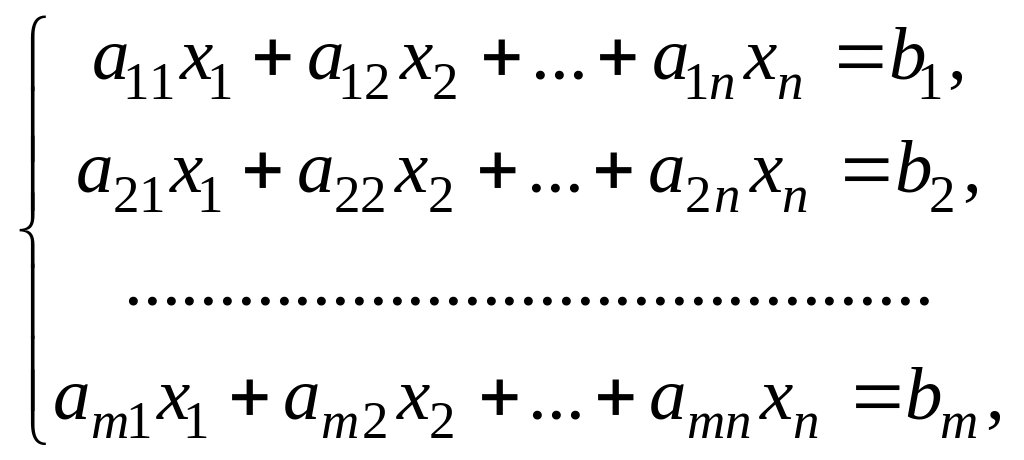(4.1)

где числа а_ij (i = 1, 2, … , m; j = 1, 2, … n) называются коэффициентами при неизвестных, b_i (i = 1, 2, …, m) – свободными членами. Число m может быть больше, равно или меньше n.

Решением системы линейных уравнений (4.1) называется всякая упорядоченная совокупность n чисел, которая, будучи подставленной в систему (4.1), вместо х_1, х₂, …, х_n обращает все уравнения в верные тождества.

Система уравнений называется совместной, если она имеет хотя бы одно решение. Система, не имеющая ни одного решения, называется несовместной. Совместная система, имеющая одно решение, называется определенной, если решений множество – неопределенной.

Введем обозначения в системе линейных уравнений (4.1). Матрица

А =

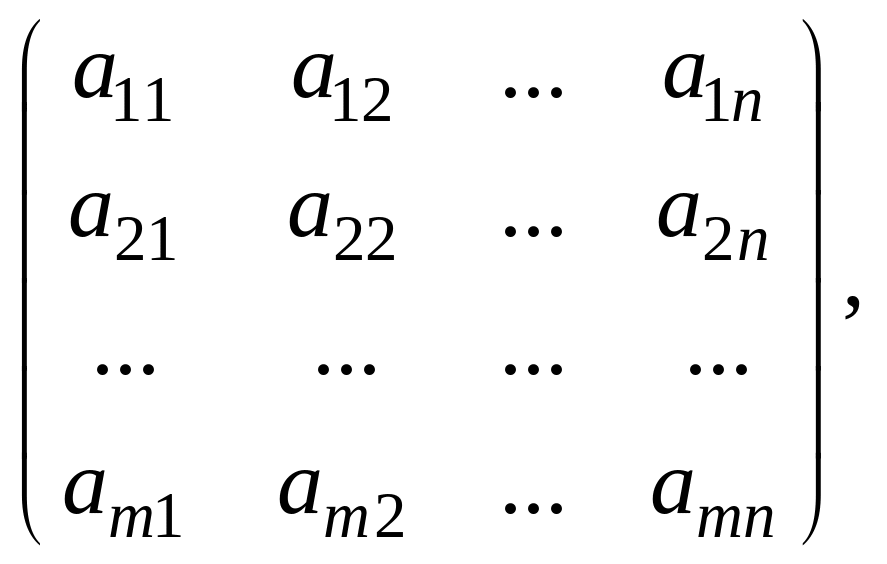
составленная из коэффициентов при неизвестных, называется основной матрицей системы или матрицей коэффициентов.

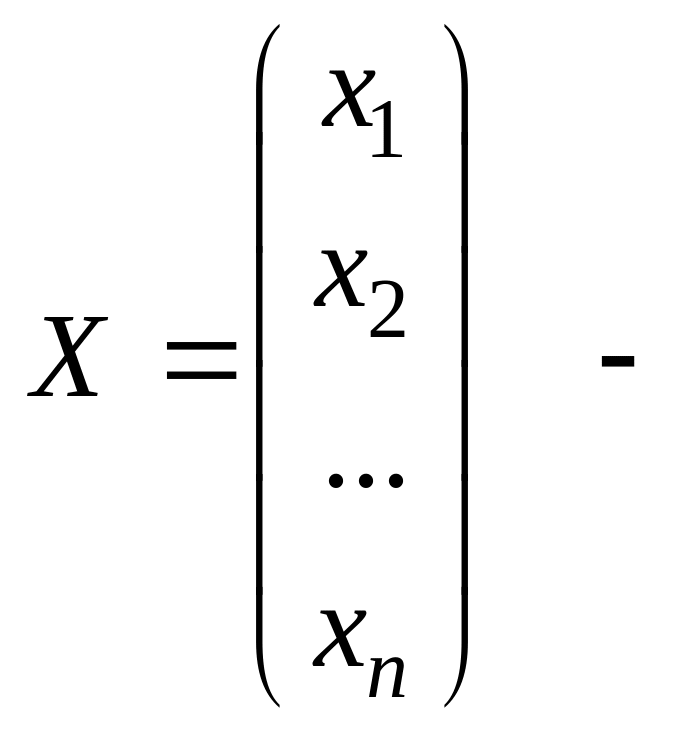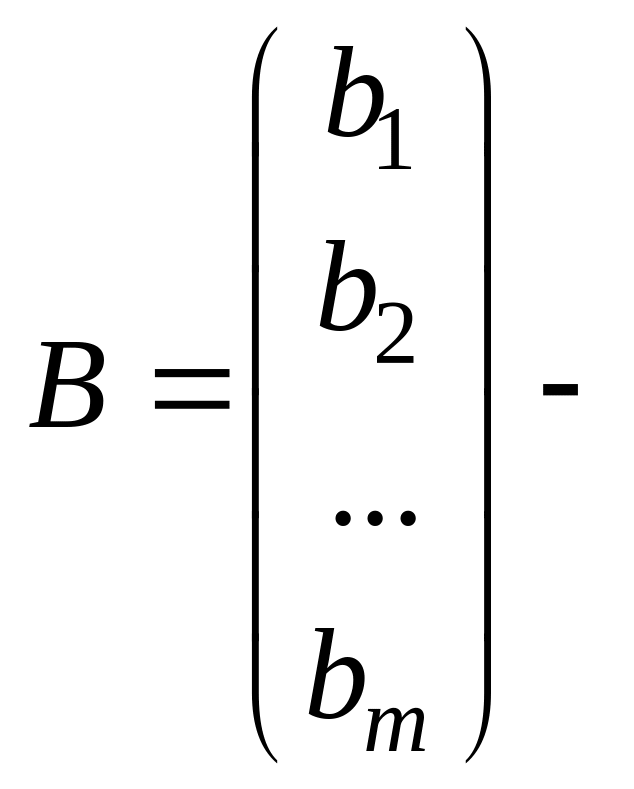матрица-столбец неизвестных, матрица-столбец свободных членов.

Матрица , полученная присоединением к матрице A столбца из свободных членов, называется расширенной матрицей системы (4.1):

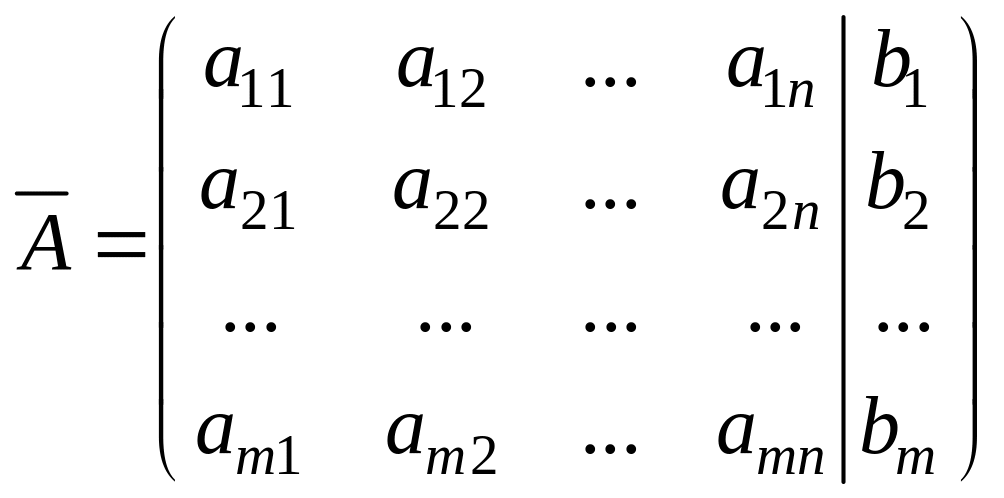
Систему (4.1) можно записать в виде матричного уравнения

A ∙B=X. (4.2)

Две системы уравнений являются равносильными, или эквивалентными, если любое решение одной системы является также решением другой системы.

Согласно теореме Кронекера-Капелли, для того чтобы система (4.1) была совместной, необходимо и достаточно, чтобы ранг основной матрицы системы был равен рангу расширенной матрицы системы:

rang A = rang .

Если rang A = rang = n, то система имеет единственное решение, если rang A = rang < n, то система имеет множество решений.

Для решения систем линейных уравнений применяются следующие методы:

1. метод Гаусса,

2. матричный метод,

3. метод Крамера.

Суть метода Гаусса состоит в том, что посредством последовательного исключения неизвестных система линейных уравнений (4.1) преобразуется в эквивалентную ей систему трапецевидной формы:

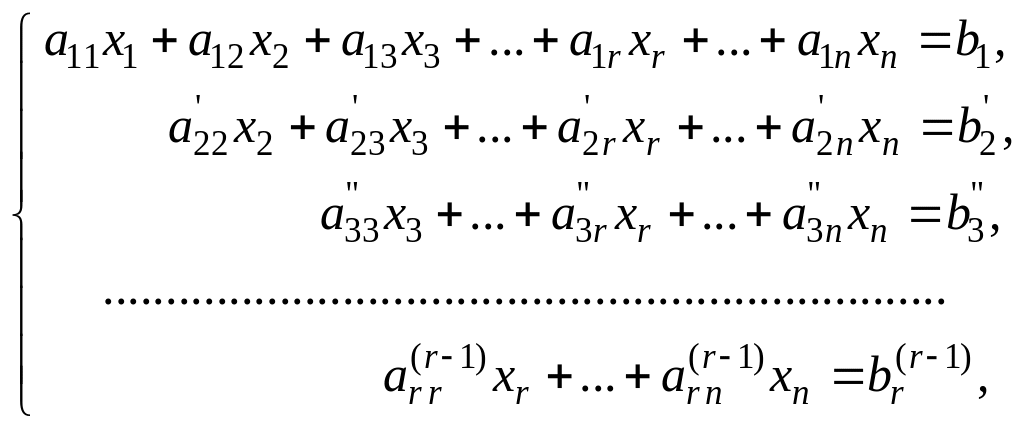(4.3)

где а₁₁, а'₂₂, а"₃₃, …, ≠ 0, r ≤ m, r ≤ n. Такие системы легко исследуются и решаются.

Для того чтобы перейти от системы (4.1) к системе (4.3), выполняют следующие преобразования:

– меняют местами уравнения системы;

– обе части уравнения умножают на число λ ≠ 0;

– прибавляют к одному уравнению другое, умноженное на некоторое число λ ≠ 0;

– меняют местами переменные в системе.

В процессе преобразования может получиться уравнение, левая и правая части которого равны нулю. Его можно отбросить, так как такое уравнение справедливо при любых значениях переменных. Если в процессе преобразования получено уравнение с нулевой левой частью и ненулевой правой, то система (4.1) несовместна, так как уравнение не имеет решения. Система, которая совместна, может быть приведена к виду (4.3). Дальнейшее решение системы зависит от того, справедливо или нет равенство r = n.

Если r = n (в этом случае говорят, что полученная система имеет треугольный вид), то все значения переменных находим с помощью «обратного хода». Система в этом случае имеет единственное решение.

Если r < n, то исходная система будет приведена к трапециевидной форме. Для решения такой системы члены, содержащие x_r+1, …, x_n (назовем их свободными переменными), переносят в правую часть.

Полученная система уравнений относительно переменных x₁, x₂, …, x_r имеет треугольный вид и x₁, x₂, …, x_r единственным образом выражаются через x_r+1, …, x_n. В этом случае система имеет бесконечное количество решений, т.к. свободным переменным можно придавать любые значения.

Пример 1. Решить систему уравнений методом Гаусса:

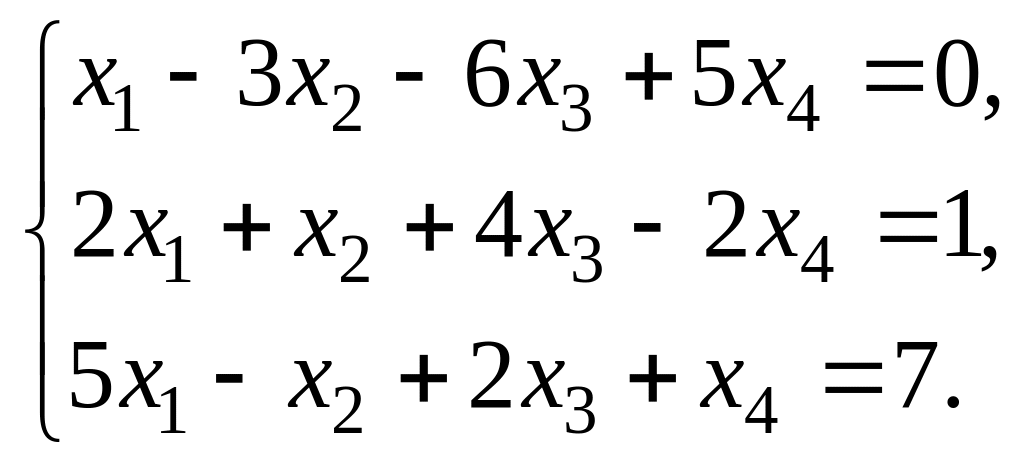
Решение. Первый шаг. Будем исключать x₁ из второго и третьего уравнений системы. В роли «ведущего» уравнения (уравнения, в котором эту переменную оставляют) выберем первое, так как а₁₁ = 1 ≠ 0 (при этом множители λ будут целыми). Для исключения х₁ из второго уравнения прибавим к нему ведущее уравнение, умноженное на (–2). Для исключения х₁ из третьего уравнения прибавим к нему ведущее уравнение, умноженное на (–5). Получим систему:

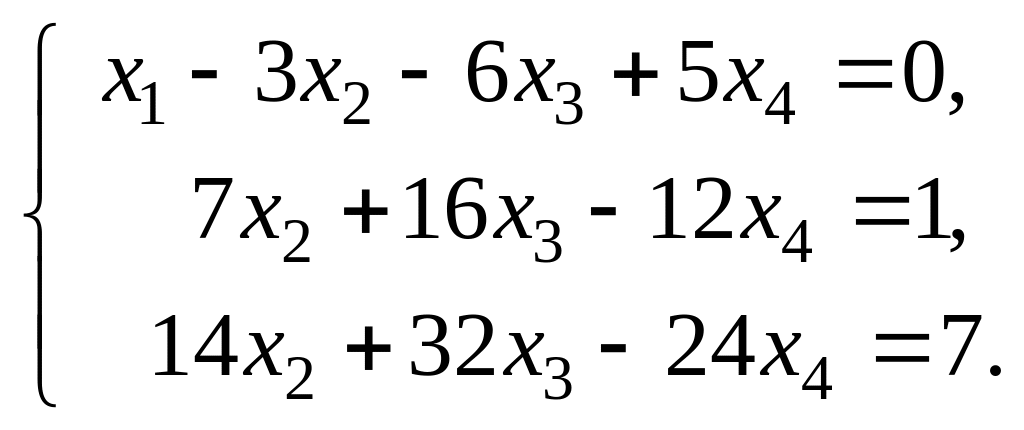
Второй шаг. Будем исключать переменную х₂ из третьего уравнения полученной системы. «Ведущим» выберем второе уравнение, где а₂₂ = 7 ≠ 0 . Умножим ведущее уравнение на (–2) и прибавим его к третьему уравнению:

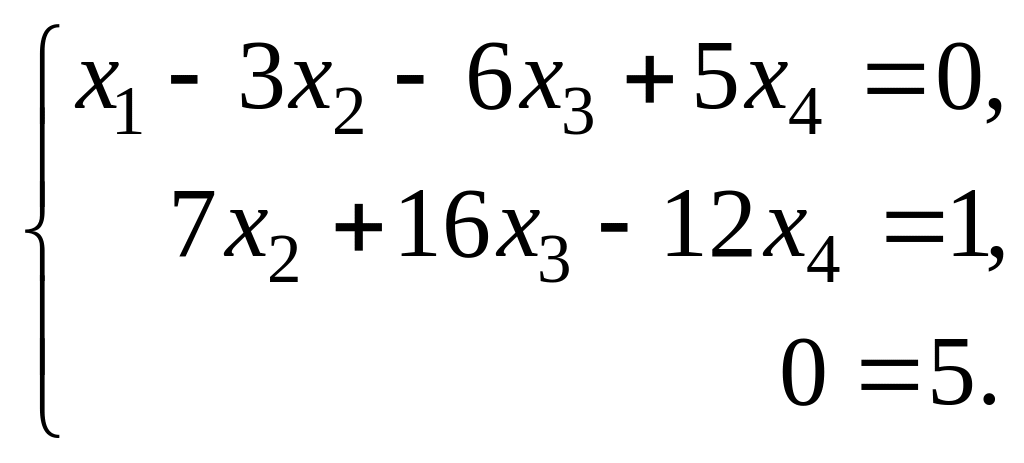
Полученная система несовместна, следовательно, несовместна и исходная система, так как эти системы эквивалентны.

Эквивалентные преобразования системы линейных уравнений удобнее выполнять с использованием расширенной матрицы коэффициентов .

Пример 2. Доказать совместность и решить методом Гаусса систему линейных уравнений:

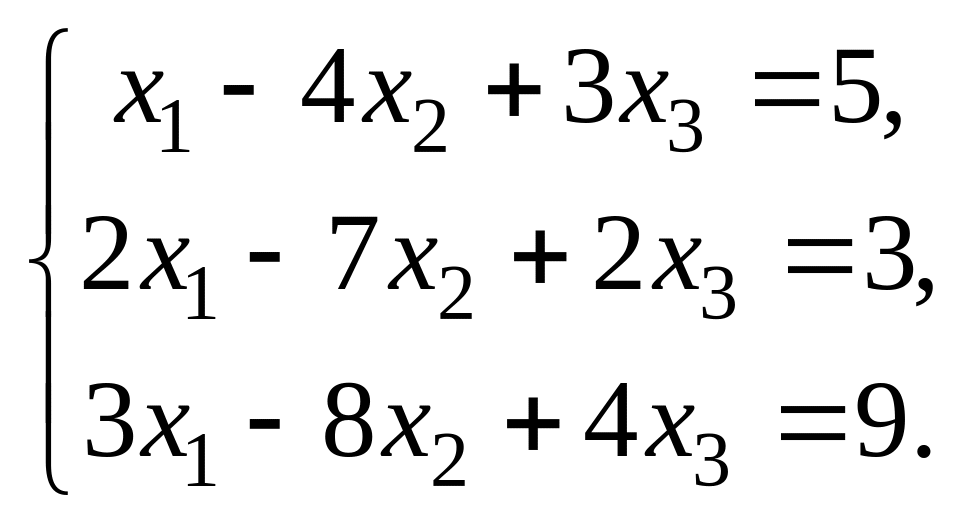
Решение. Составим расширенную матрицу системы и найдем ее ранг. Для этого произведём над её строками элементарные преобразования (строку, которую умножаем на λ ≠ 0 и складываем с другой строкой, будем обозначать ″стрелочкой″):

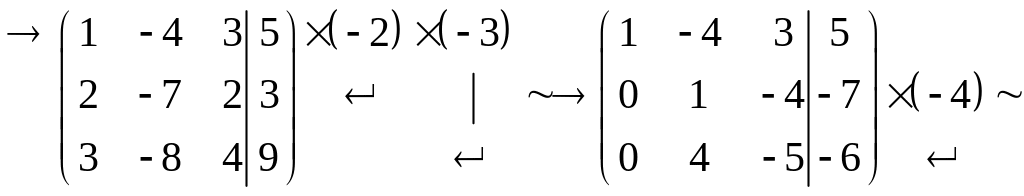
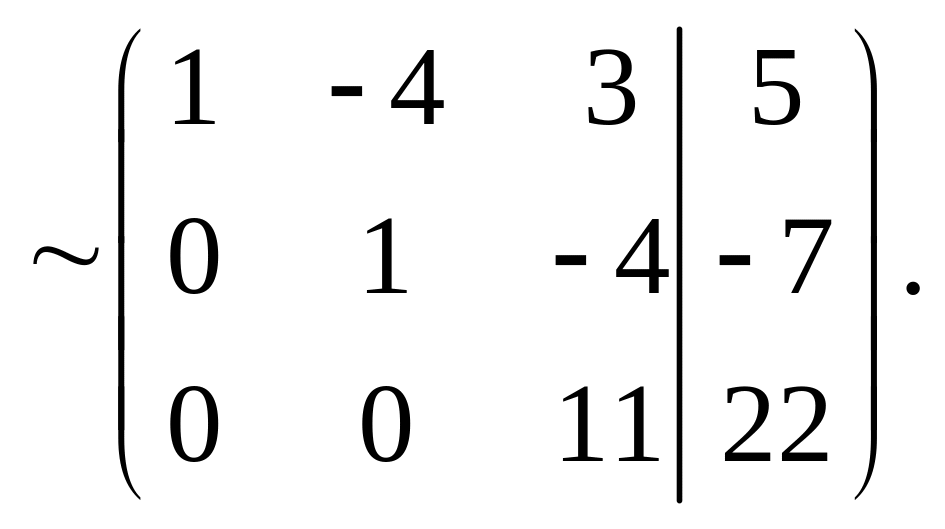
Первую строку умножили последовательно на (–2) и на (–3) и сложили с соответствующими элементами второй и третьей строк. Затем элементы второй строки умножили на (–4) и сложили с соответствующими элементами третьей строки.

Полученная матрица треугольного вида, rang A = rang =3. По теореме Кронекера-Капелли система совместна. Ранг системы r = 3 и равен числу неизвестных n = 3, поэтому система имеет единственное решение, то есть определена.

Последней матрице соответствует система вида

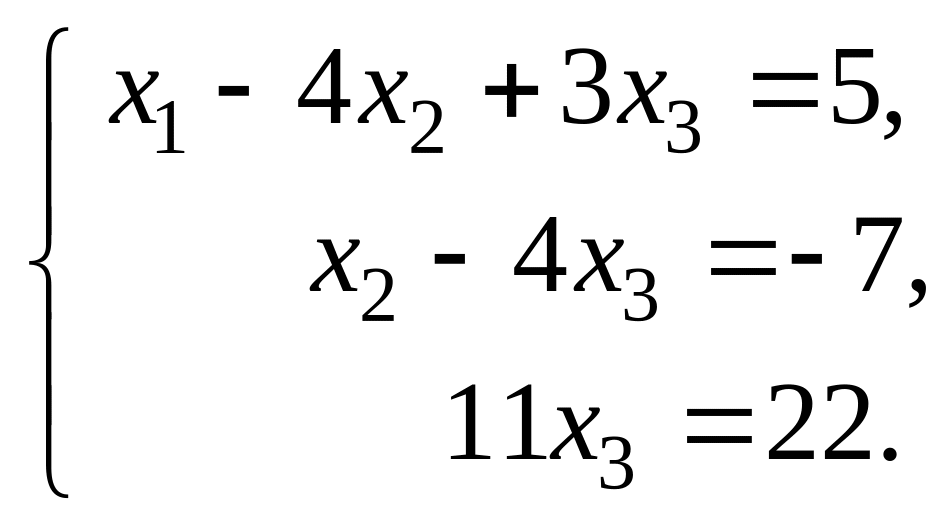
Найдём её решение с помощью «обратного хода» метода Гаусса. Из последнего уравнения вычисляем x₃ = 22/11 = 2. Подставим это значение x₃ = 2 во второе уравнение и рассчитаем x₂: х₂ = 4х₃ – 7 = 1. Из первого уравнения системы найдём значение х₁: х₁= 4x₂ –3x₃ +5 = 4·1 –3·2 +5=3. Итак, решение системы x₁ = 3; x₂ = 1; x₃ = 2.

Система (4.1) в случае, когда т = п имеет вид:

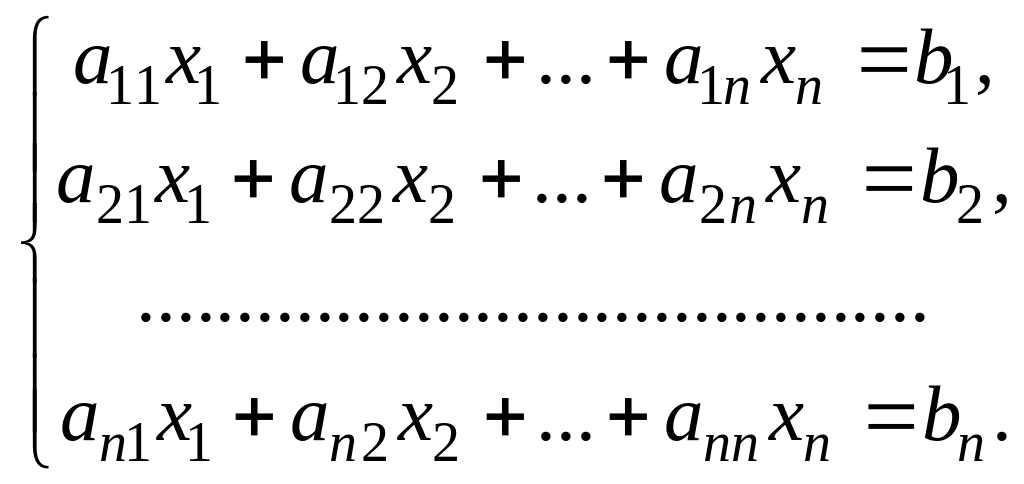(4.4)

Матрица коэффициентов А является квадратной матрицей порядка п. Когда она невырожденная для нее существует единственная обратная матрица А^–1 , определяемая формулой (3.1).

Найдем решение системы (4.4), представленное в виде матричного уравнения:

A ∙ X=B.

Умножив обе части уравнения слева на обратную матрицу А^–1, получим

А^–1 ·A·X = А^–1 ·B.

Так как А^–1 · А = А· А^–1 = E, то

X = А^–1·B. (4.5)

Метод решения системы линейных уравнений с использованием формулы (4.5) называется матричным. Рассмотрим работу метода на примере.

Пример 3. Решить систему матричным методом уравнений

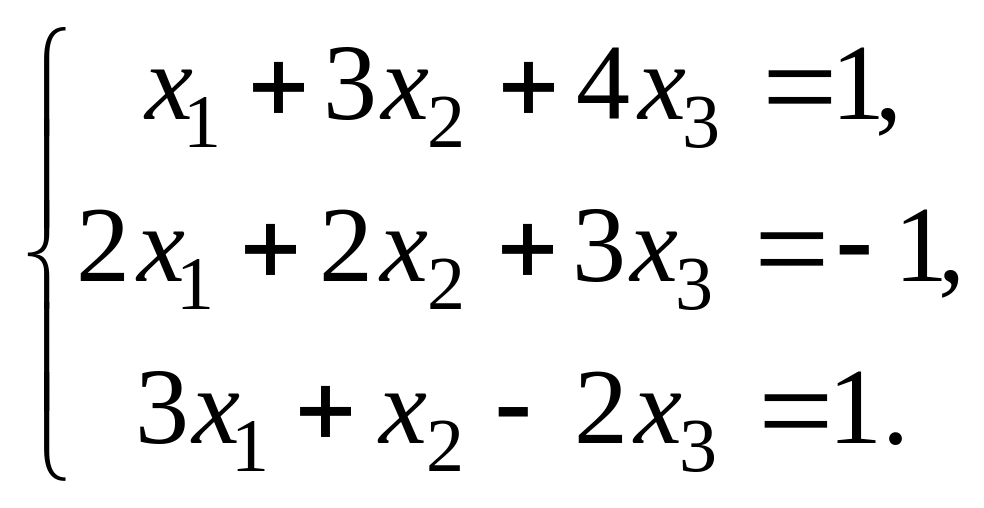
Решение. Сначала вычислим определитель матрицы А:

|А| =

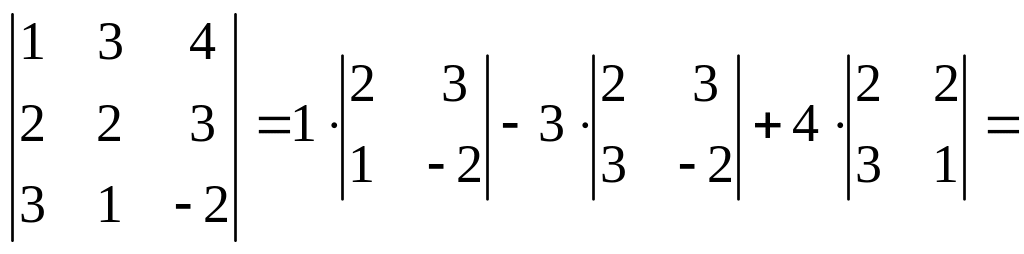
= – 7 + 39 – 16 = 16 ≠ 0

(определитель рассчитали разложением по элементам первой строки по формуле (2.2)). Так как |А| ≠ 0, матрица А является невырожденной и для нее можно найти А^–1.

Вычислим алгебраические дополнения А_ij элементов матрицы А по формуле (2.1):

А₁₁ = = –7; А₂₁ = = 10; А₃₁ = = 1;

А₁₂ = = 13; А₂₂ = = – 14; А₃₂ = = 5;

А₁₃ = = – 4; А₂₃ = = 8; А₃₃ = = –4.

По формуле (3.1) составляем обратную матрицу:

А^–1 =

Для нахождения матрицы-решения X умножим обратную матрицу А^–1 на матрицу-столбец свободных членов системы В:

X = А^–1·B =

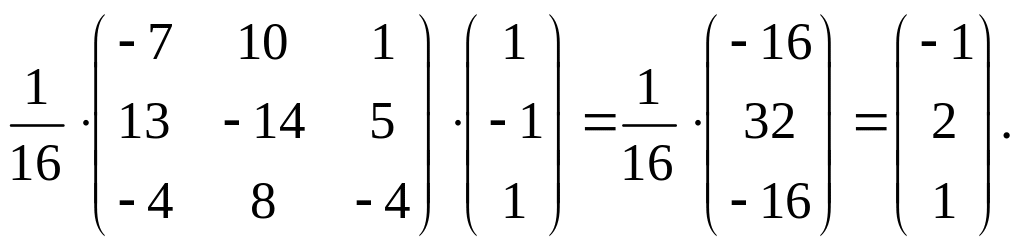
Отсюда, x₁ = –1; х₂ = 2; х₃ = –1.

Упорядоченная тройка чисел (–1; 2; –1) – есть решение данной системы уравнений.

Систему линейных уравнений (4.4) также можно решить методом Крамера. Для этого составляют главный определитель системы (4.4) из коэффициентов, стоящих при переменных:

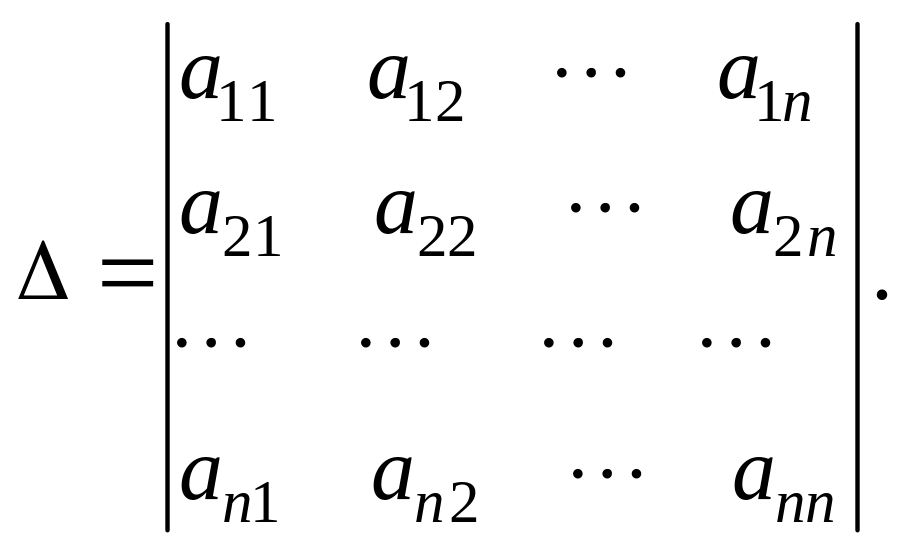
Следует отметить, что система (4.4) будет иметь единственное решение, если главный определитель не равен нулю (∆ ≠ 0). Затем составляют n вспомогательных определителей ∆_i ( i = 1, 2, …, n). Вспомогательный определитель ∆_i получают заменой в главном определителе i – того столбца на столбец свободных членов:

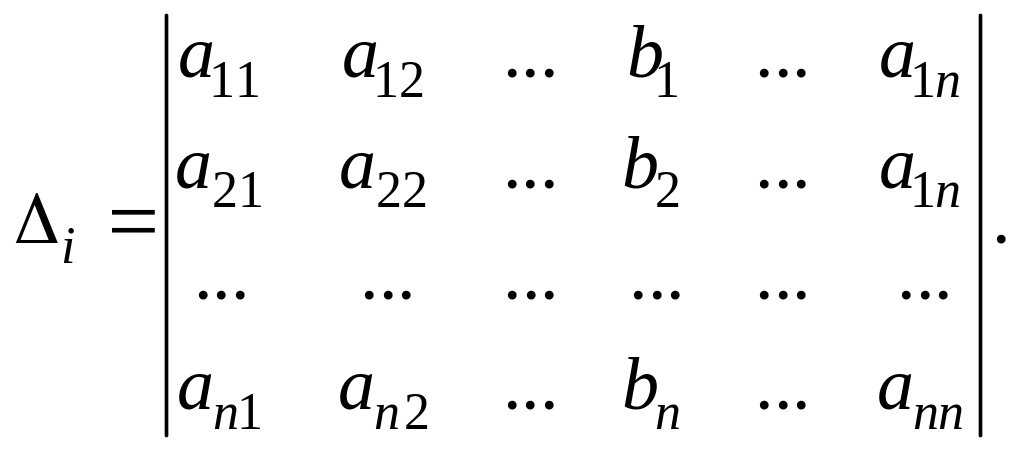
Решение системы (4.4) находят по формулам Крамера, как отношение соответствующего вспомогательного определителя к главному:

Пример 4. Решить методом Крамера систему линейных уравнений

Решение. Найдем значение главного определителя системы:

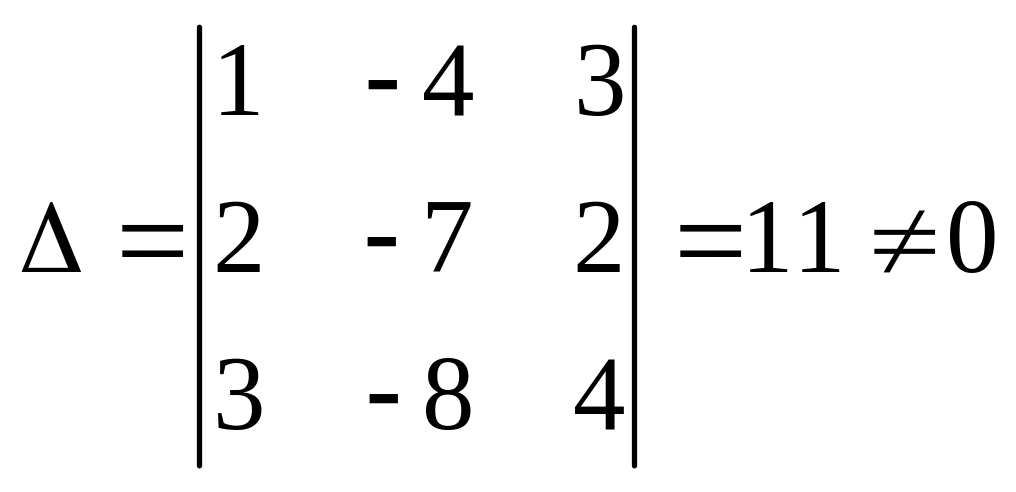( следовательно, система уравнений совместна и имеет единственное решение).

Составим и вычислим три вспомогательных определителя:

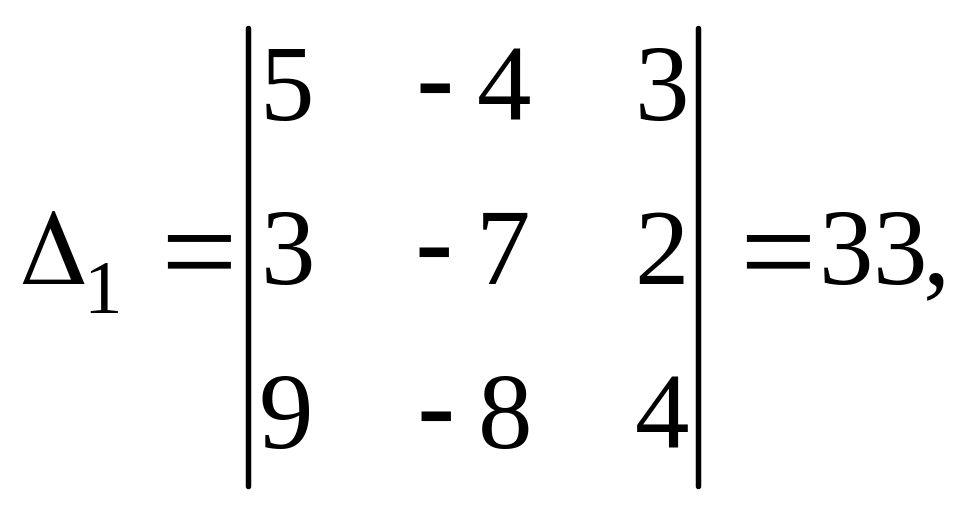
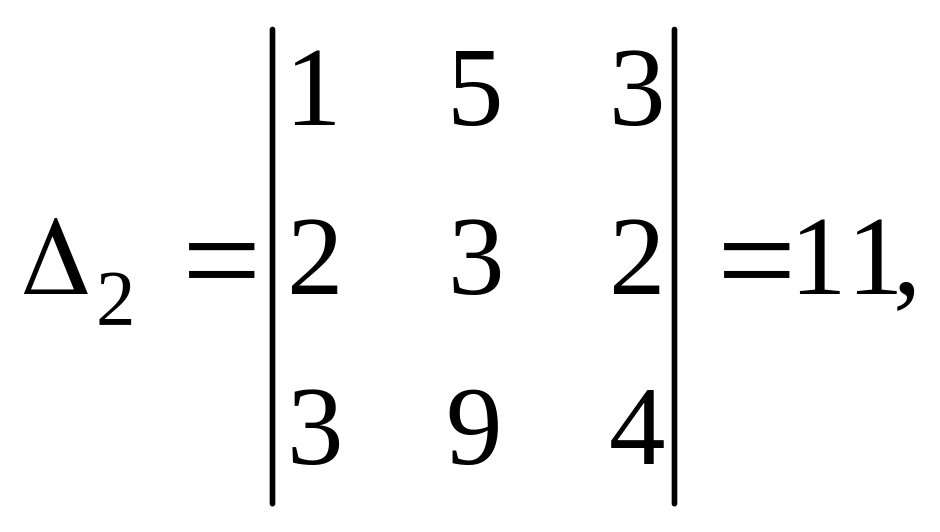
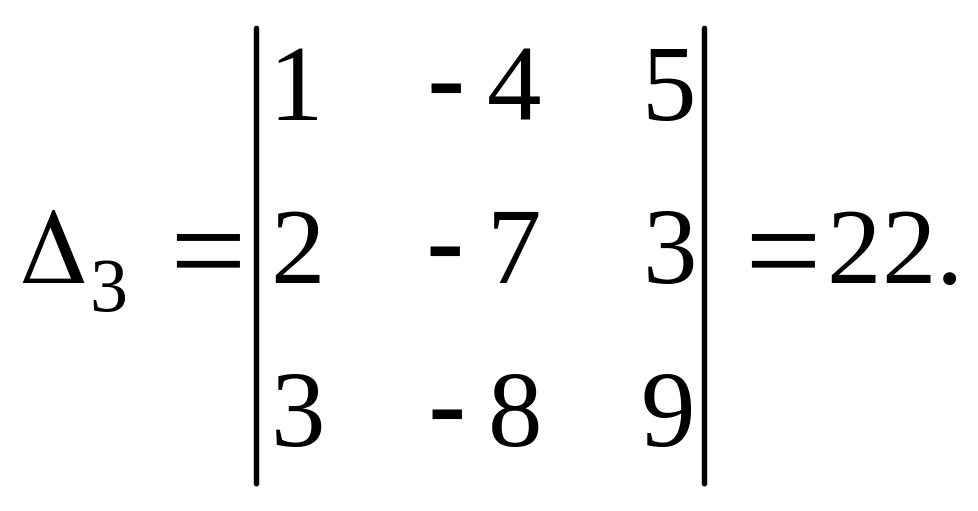
Решение системы:

Пример 5. Дана система линейных уравнений

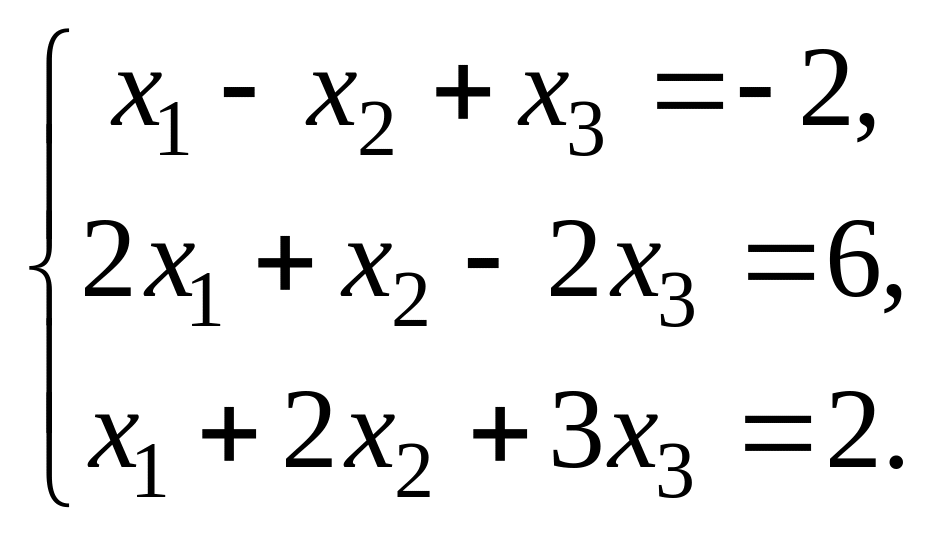
Доказать её совместность и решить тремя способами: 1) методом Гаусса; 2) матричным методом; 3) методом Крамера. Проверить правильность вычисления обратной матрицы, используя матричное умножение.

Решение. Выпишем расширенную матрицу системы и проведём элементарные преобразования для приведения матрицы к треугольному или трапециевидному виду, из которых легко находится ранг матрицы системы:

=

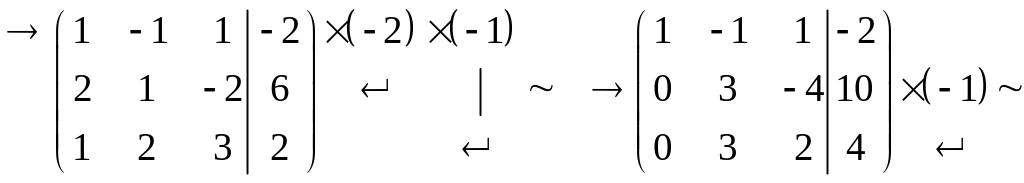
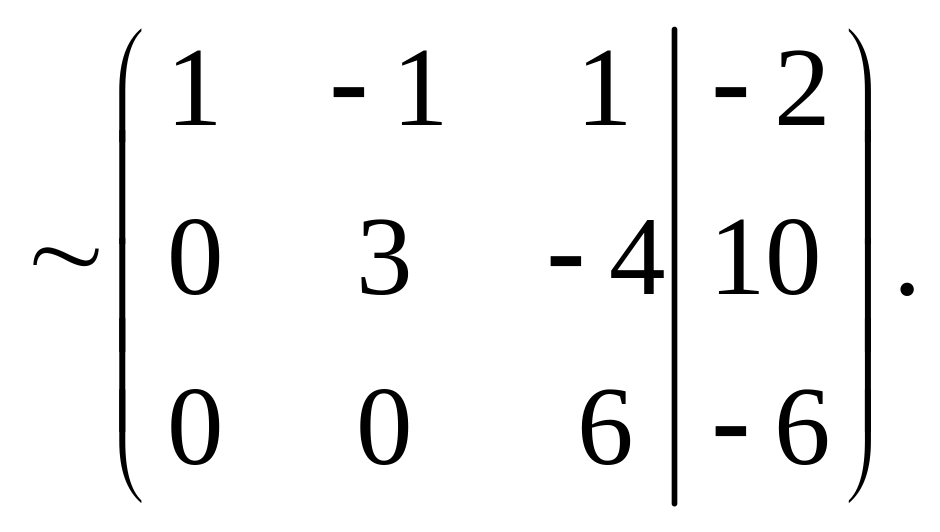
Полученная матрица эквивалентна матрице .Эта трапециевидная матрица имеет три ненулевых строки, следовательно, её ранг равен трём: rang =3. Это значит, что существует минор третьего порядка, отличный от нуля, например:

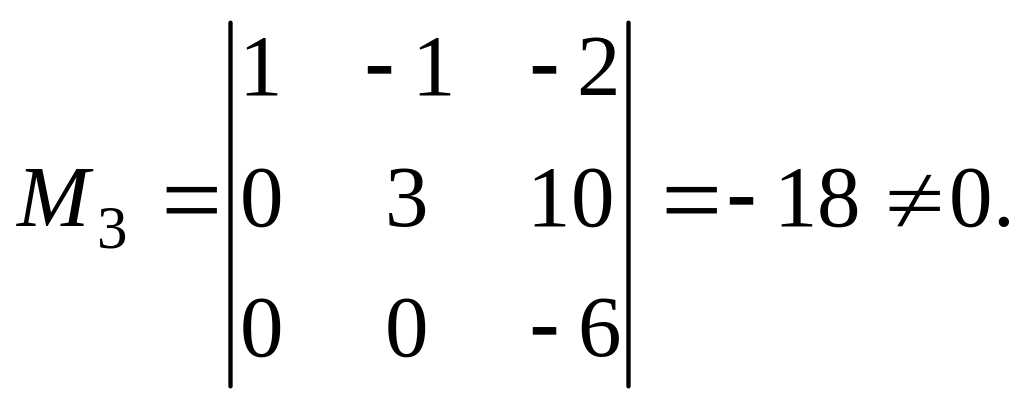
Ранг основной матрицы системы А также равен трём, так как M₃ входит и в основную матрицу. Поскольку rang A = rang , то система линейных уравнений совместна. Так как ранги равны числу неизвестных, система имеет единственное решение.

1) Решим данную систему методом Гаусса.

Произведя над расширенной матрицей системы элементарные преобразования, мы получили эквивалентную ей матрицу:

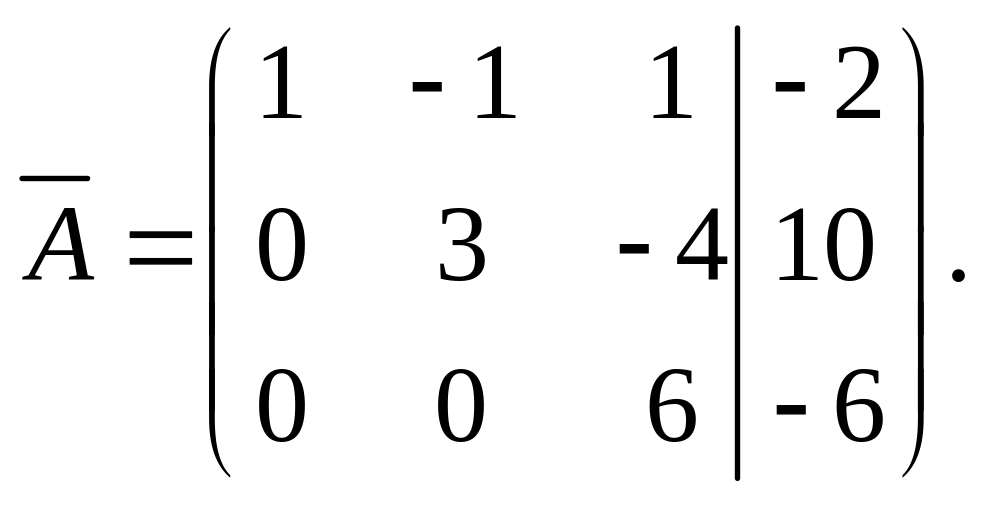
Последней матрице соответствует система вида

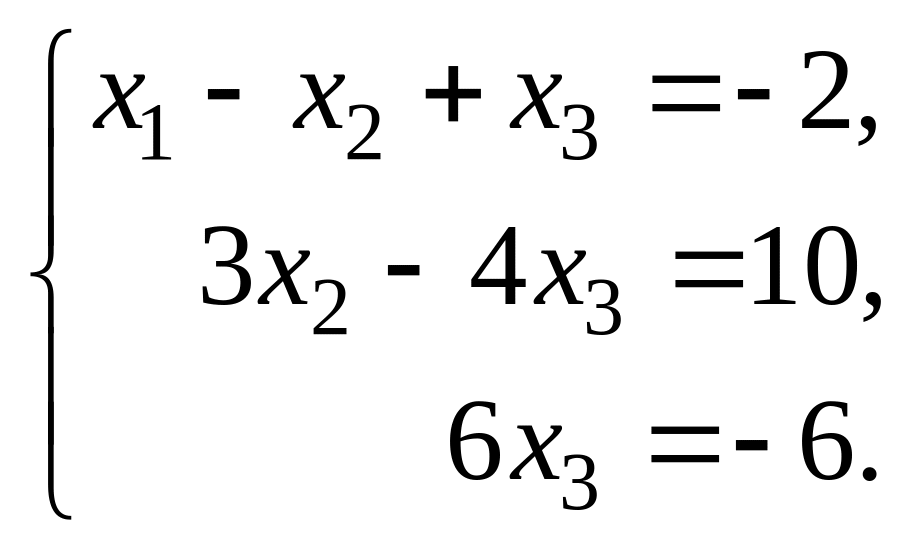
Найдём её решение с помощью «обратного хода» метода Гаусса. Из последнего уравнения определим х₃ = –6/6 = –1. Подставим это значение х₃ = –1 во второе уравнение и найдём из него х₂:

х₂ =

Из первого уравнения системы вычислим значение х₁:

х₁ = х₂ – х₃ – 2 = 2 + 1 – 2 = 1.

Итак, решение системы (1; 2; –1).

2) Решение системы матричным методом находят по формуле (4.5). Запишем матрицу коэффициентов системы

A=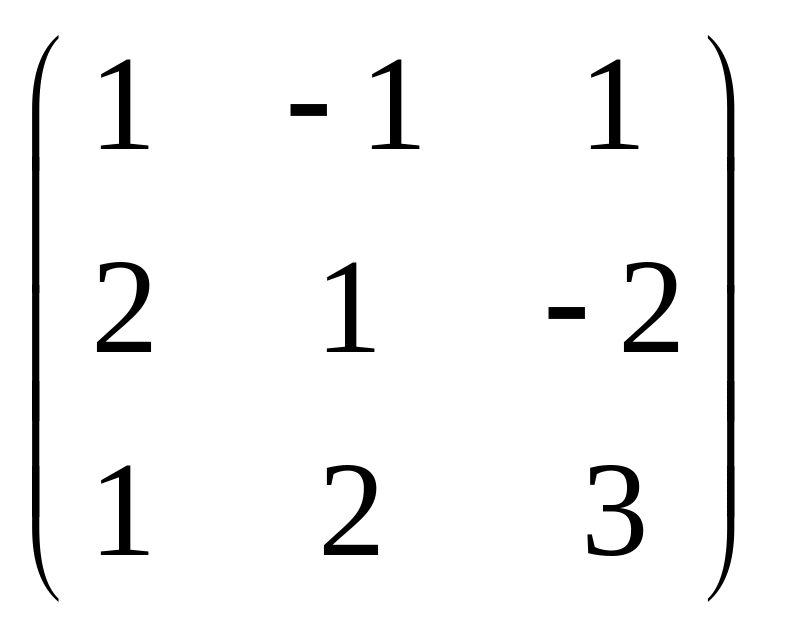 и матрицу-столбец свободных членов .

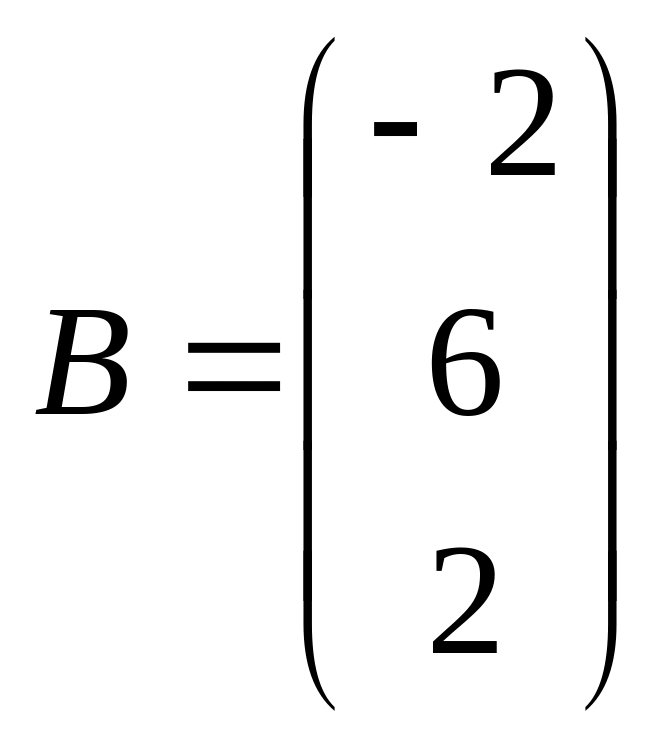Вычислим определитель матрицы А:

|А| =

= 7 + 8 + 3 = 18 ≠ 0

(определитель рассчитали разложением по элементам первой строки по формуле (2.2)). Так как |А|≠ 0, матрица А является невырожденной и для нее можно найти А^–1.

Вычислим алгебраические дополнения А_ij элементов матрицы А по формуле (2.1):

А₁₁ = = 7; А₂₁ = = 5; А₃₁ = = 1;

А₁₂ = =–8; А₂₂ = = 2; А₃₂ = = 4;

А₁₃ = = 3; А₂₃ = = –3; А₃₃ = = 3.

По формуле (3.1) составляем обратную матрицу:

А^–1 =

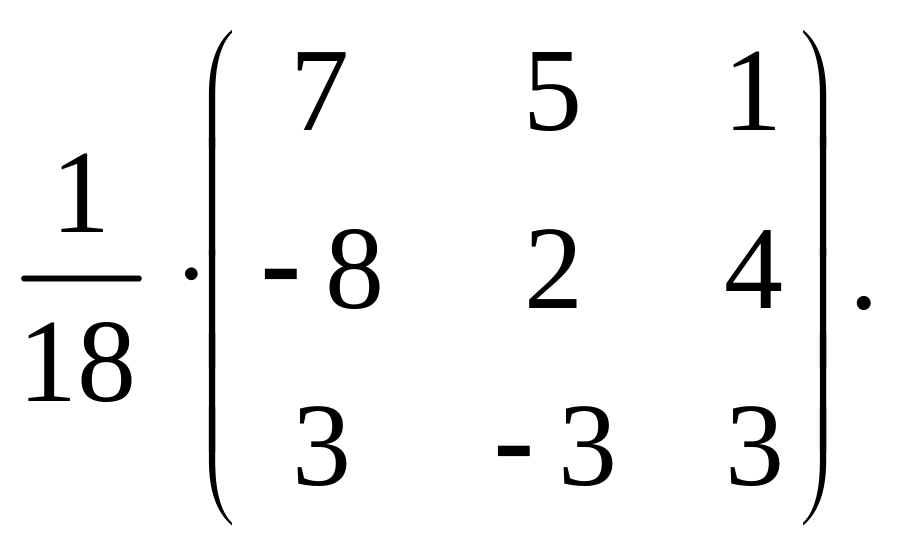
Проверим правильность вычисления A^–1:

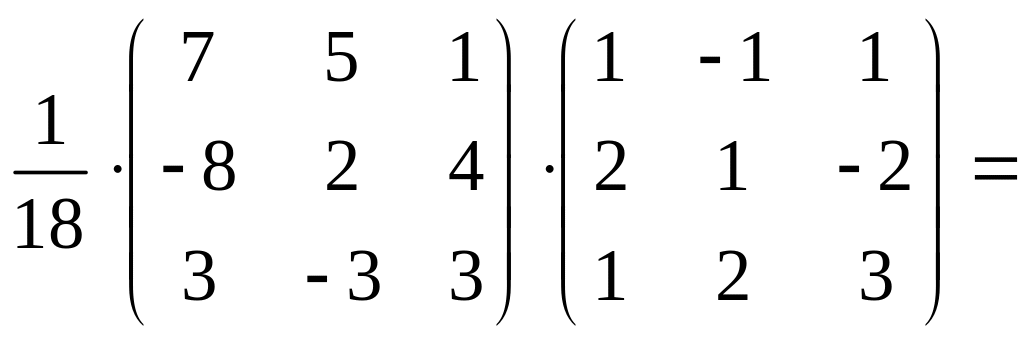
A^–1 ·A = = = E.

Для нахождения матрицы-решения X умножим обратную матрицу А^–1 на матрицу-столбец свободных членов системы В:

X = А^–1·B =

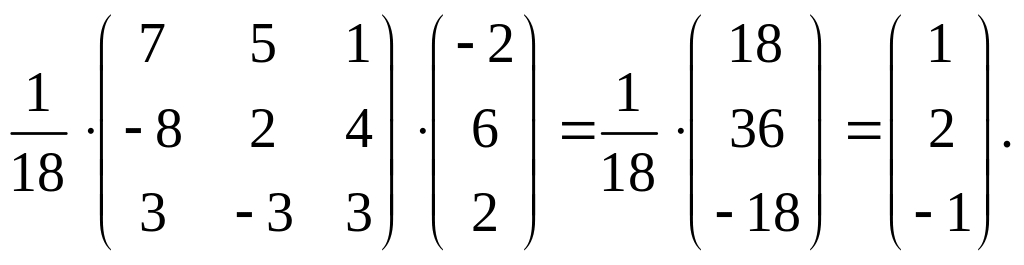
Отсюда, x₁ = 1; х₂ = 2; х₃ = –1.

3)Для решения системы уравнений методом Крамера вычислим главный определитель:

Δ=|А| = 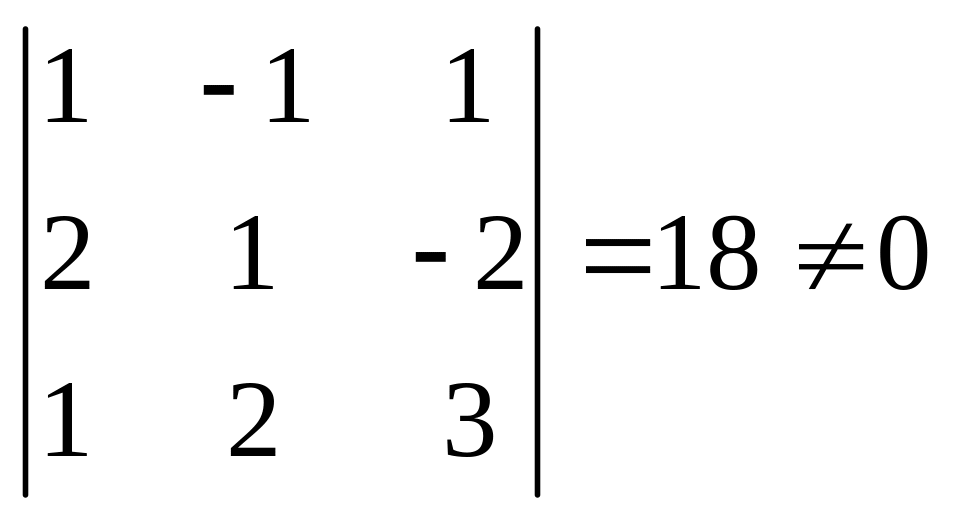,следовательно, система имеет единственное решение.

Составим и вычислим три вспомогательных определителя:

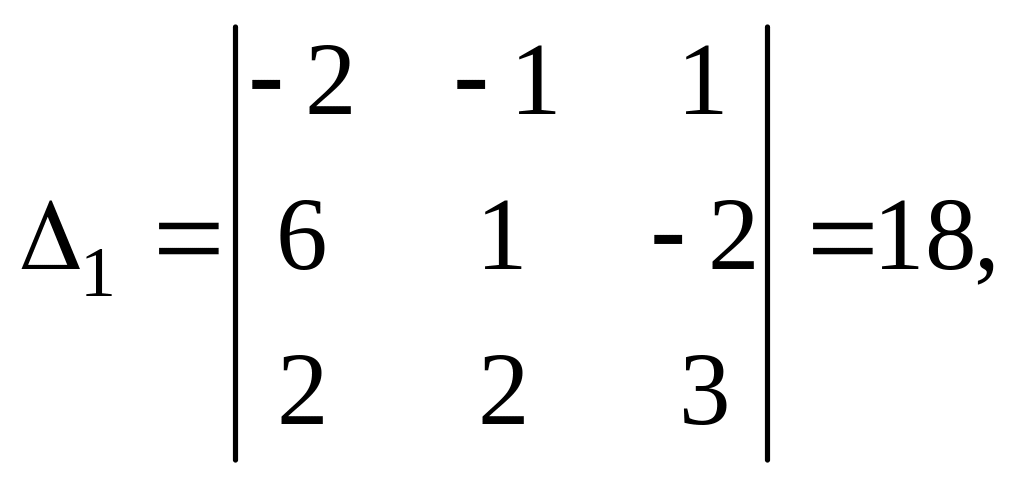
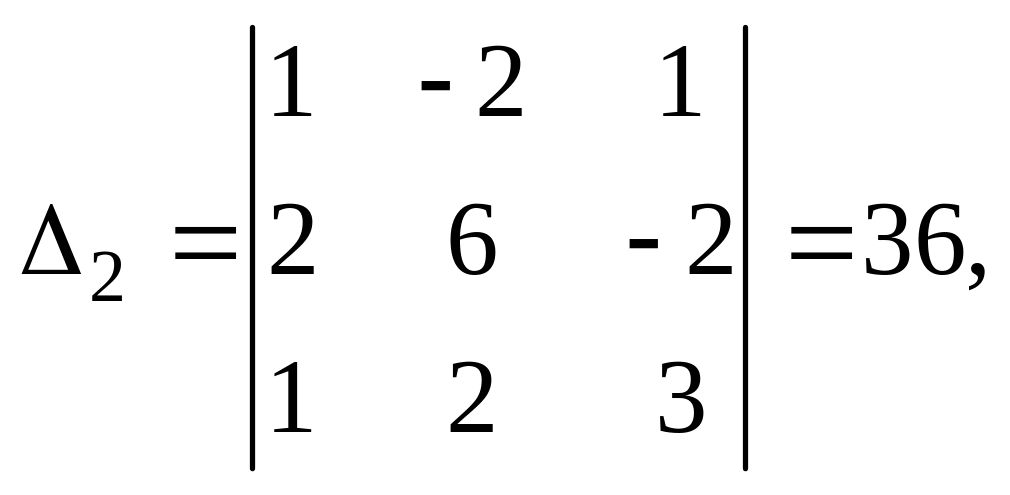
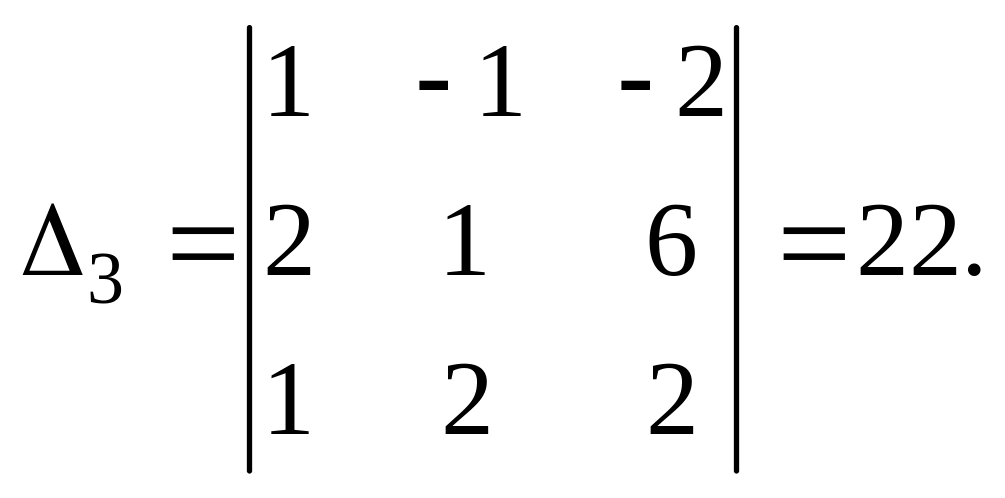
Решение системы:

; ; .

Разобранный выше пример применим в качестве образца для решения номеров 51 -60 контрольной работы № 1.