2. Определители и их вычисление

Понятие определителя вводится только для квадратной матрицы. Это число, которое ставится в соответствие данной матрице А и обозначается d(A), |А|, det А или

Δ =

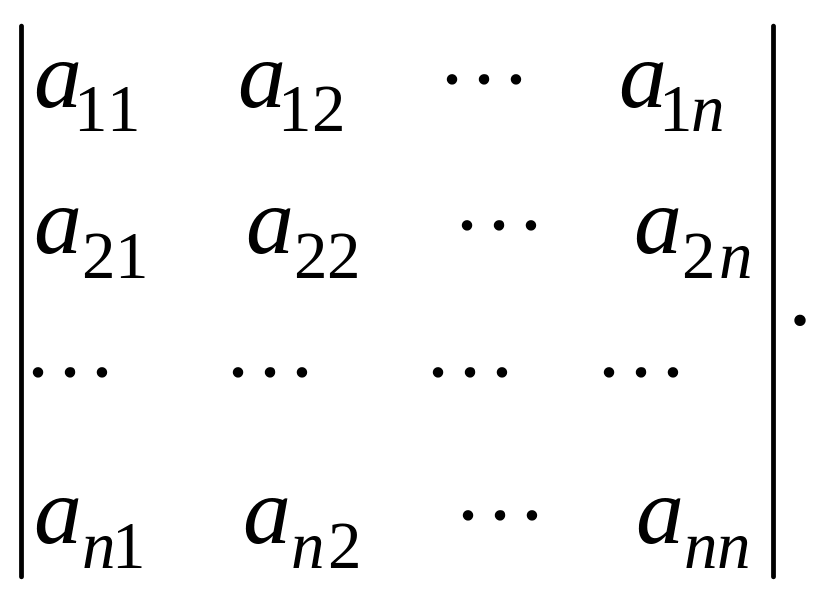
Определителем матрицы А_1×1, состоящей из одного числа, называется само число: |А| = а₁₁.

Определителем второго порядка называется число, равное разности произведений элементов главной и побочной диагоналей:

Δ = а₁₁ а₂₂ – а₁₂ а₂₁.

Определителем третьего порядка, соответствующим матрице третьего порядка, называется число, равное

Δ = 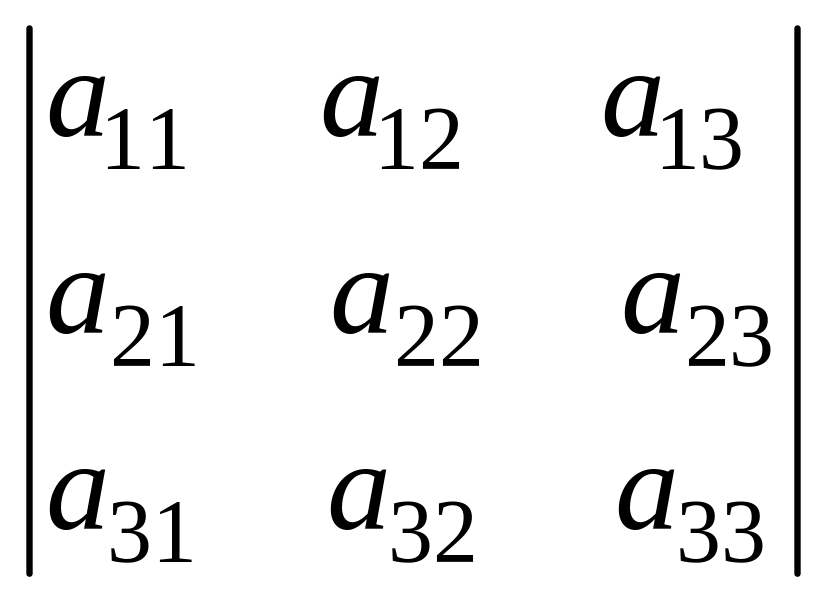= а₁₁ а₂₂ а₃₃ + а₁₂ а₂₃ а₃₁ + а₂₁ а₃₂ а₁₃ –

– а₁₃ а₂₂ а₃₁– а₃₂ а₂₃ а₁₁ – а₂₁ а₁₂ а₃₃.

Пример 1. Вычислить определитель матрицы А:

а) ; б) .

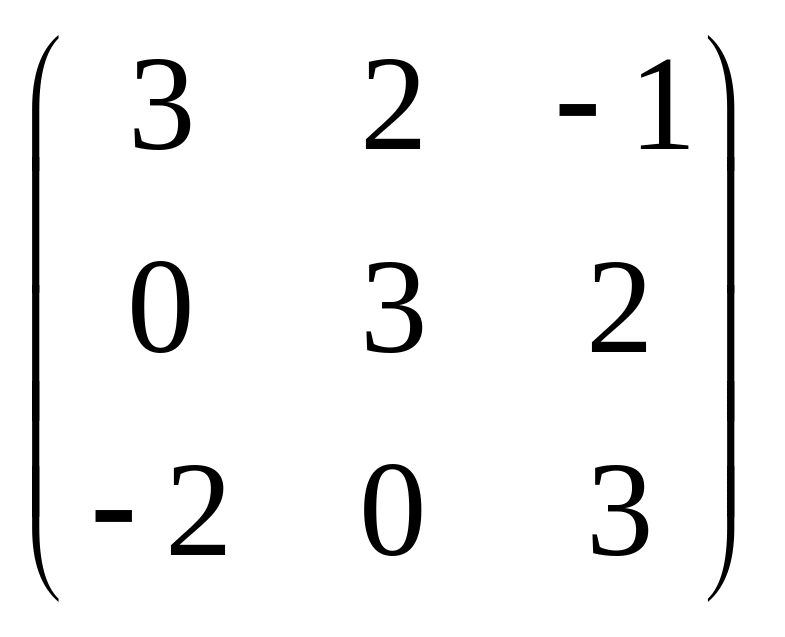Решение:

а) Δ= 6·4 – (– 1)·1 = 24 + 1 = 25;

б) Δ= 3·3·3 + 2·2·( –2) + 0·0·(–1) – (–1)·3·(–2) – 0·2·3 – 0·2·3 =

= 27 – 8 + 0 – 6 – 0 – 0 = 13.

Введем несколько понятий, необходимых для вычисления определителя n-го порядка.

Минором M_ij для элемента а_ij определителя n-го порядка называется определитель (n-1)-го порядка, полученный из данного определителя вычеркиванием i-той строки и j-того столбца, на пересечении которых стоит данный элемент.

Алгебраическим дополнением А_ij для элемента а_ij определителя n-го порядка называется минор этого элемента, умноженный на (–1)^i+j, где i+j – сумма номеров строки и столбца, на пересечении которых расположен этот элемент:

А_ij = (–1)^i+j ·M_ij (2.1)

Пример 2. Найти M₃₁, А₃₁, M₃₂, А₃₂ для определителя

Δ = .

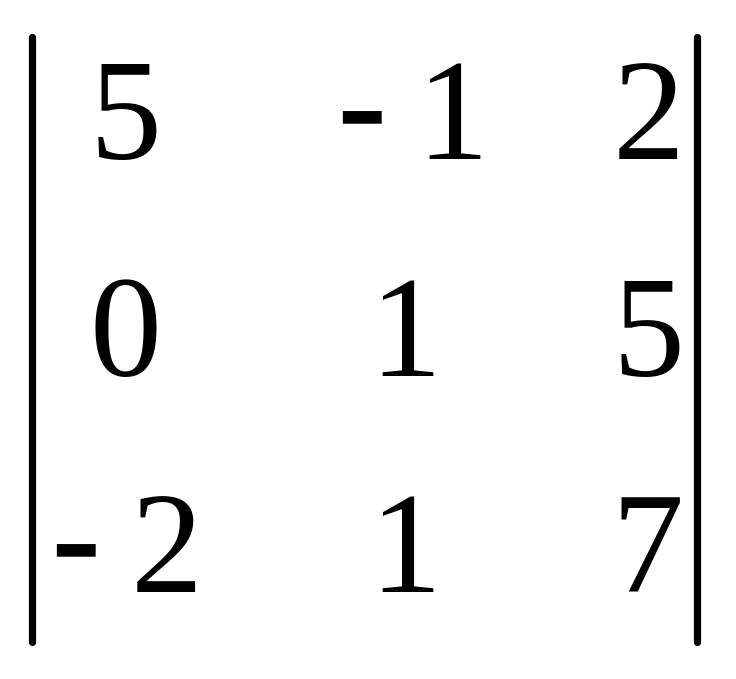Решение. Чтобы найти M₃₁, нужно из данного определителя Δ вычеркнуть третью строку и первый столбец, оставшиеся элементы записать как определитель второго порядка:

= (–1)∙5 – 2∙1 = – 5 – 2 = – 7.

По формуле (2.1) найдем А₃₁:

А₃₁ = (–1)³⁺¹ ·M₃₁ = M₃₁ = –7

Вычислим M₃₂ и А₃₂:

M₃₂ = = 5·5 – 0·2 = 25; А₃₂ = (–1)³⁺² M₃₂ = –25.

Определитель n-го порядка равен сумме произведений элементов любой строки (столбца) на алгебраические дополнения этих элементов:

Δ = а_i1 A_i1 + а_i2 A_i2 + …+ а_in A_in (2.2)

Пример 3. Вычислить определитель, разложив его по элементам первой строки.

Решение.

Δ = 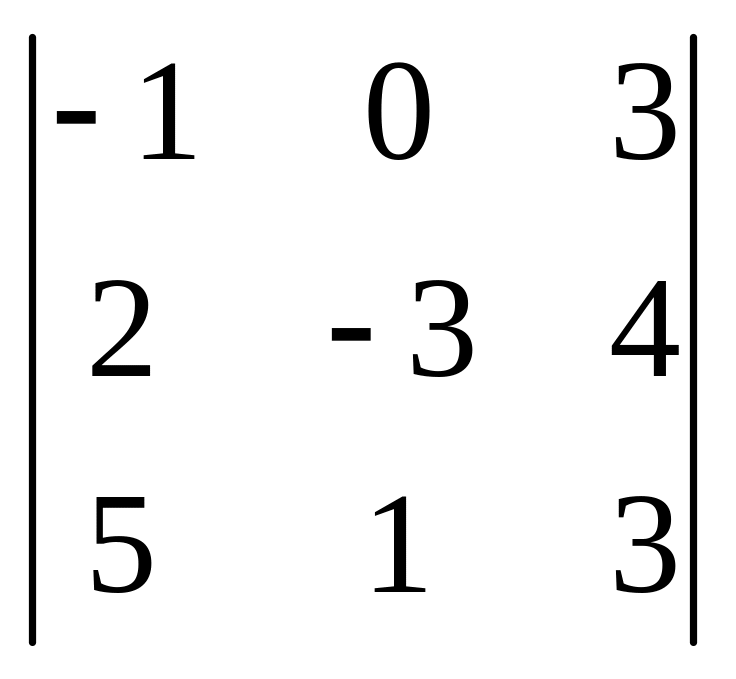= а₁₁ A₁₁ + а₁₂ A₁₂ + а₁₃ A_{13 =}

= (–1)·(–1)¹⁺¹· + 0∙ A₁₂ + 3 · (– 1)¹⁺³· =

= – ((– 3)·3 – 4 · 1) + 3∙(2·1 – (– 3)·5) = 13 + 51 = 64.

Пример 4. Вычислить определитель, разложив его по элементам второго столбца.

Решение:

Δ = 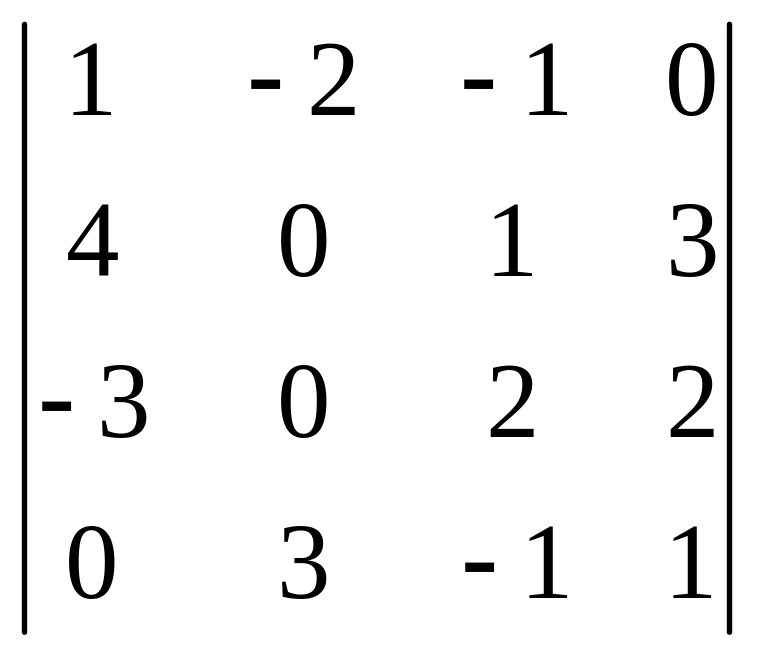= а₁₂ A₁₂ + а₂₂ A₂₂ + а₃₂ А₃₂ + а₄₂ A₄₂ =

= (– 2) ·(– 1)¹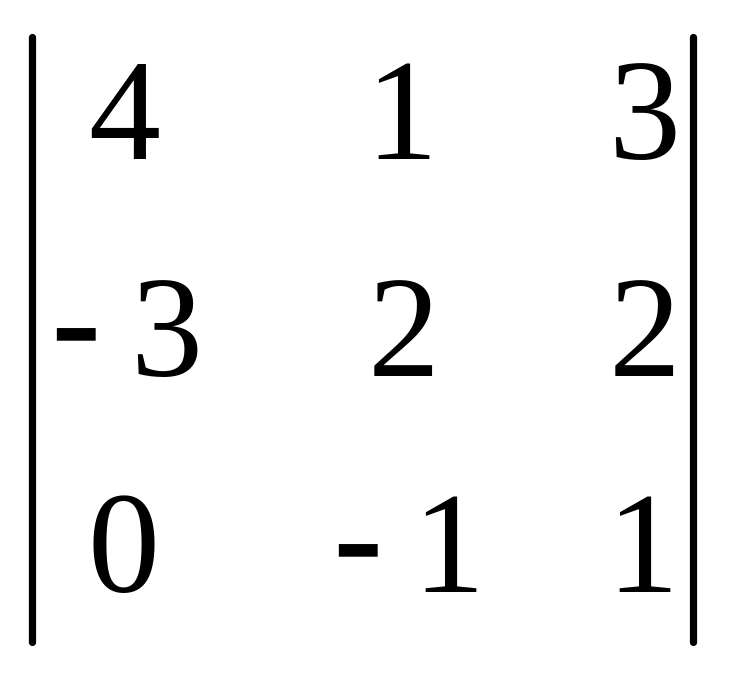⁺² · + 0·A₂₂ + 0· А₃₂ + 3·(–1)⁴⁺²· =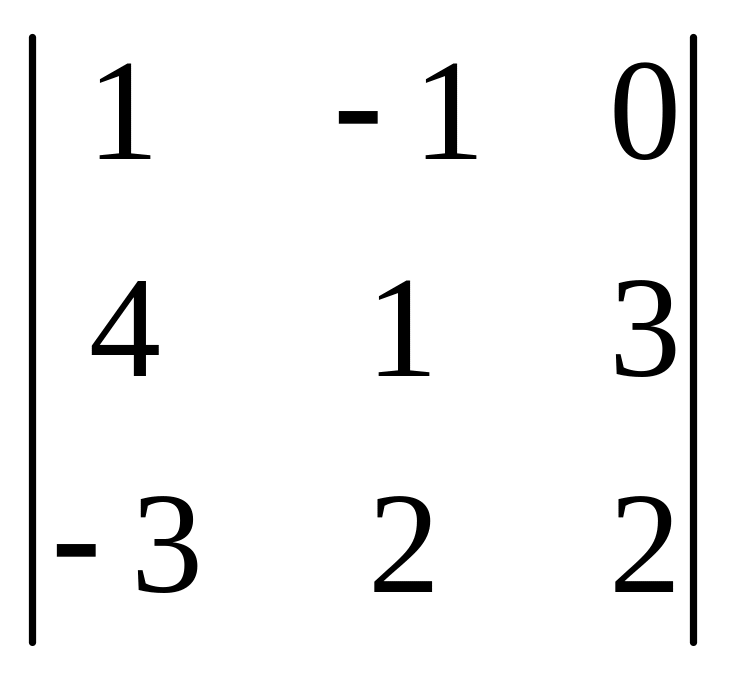

= 2∙(8 + 9 + 0 – 0 + 8 + 3) + 3∙(2 + 0 + 9 – 0 – 6 + 8) = 56 + 39 = 95.

При вычислении определителей порядка выше третьего полагается знание свойств определителей. Сформулируем эти свойства:

1. Величина определителя не изменится, если его строки и столбцы поменять местами (транспонировать).

2. При перестановке двух строк (столбцов) определителя знак определителя меняется на противоположный.

3. Определитель равен нулю:

а) если он содержит в какой-либо строке (столбце) все нули;

б) имеет две одинаковые строки (столбца);

в) имеет две строки (столбца) с пропорциональными элементами;

г) одна из строк (столбцов) есть сумма других строк (столбцов), умноженных на какие-либо числа.

4. Общий множитель элементов строки (столбца) можно вынести за знак определителя.

5. Если каждый элемент какой-либо строки (столбца) определителя представляет собой сумму двух слагаемых, то такой определитель равен сумме двух определителей, в первом из которых эта строка (столбец) содержит первые слагаемые, а во втором определителе эта строка (столбец) имеет вторые слагаемые; остальные элементы одни и те же.

6. Величина определителя не изменится, если к элементам некоторой строки (столбца) определителя прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число.

7. Сумма произведений элементов какой-либо строки (столбца) определителя на алгебраические дополнения соответствующих элементов другой строки (столбца) равна нулю.

8. Определитель произведения двух квадратных матриц А и В одного и того же порядка равен произведению их определителей:

| A∙B | = | A | ∙ | B |.