§4. Системы линейных уравнений

Уравнение – это равенство, которое содержит буквы, обозначающие неизвестные величины, эти буквы называются неизвестными. Решением уравнения называется упорядоченный набор чисел, при подстановке которых в уравнение вместо соответствующих неизвестных получается верное равенство. Решить уравнение, значит, найти множество всех его решений.

Определение 4. Системой линейных уравнений называется набор уравнений следующего вида:

а ₁₁х₁ + а₁₂х₂ + ... + а_1nх_n = b₁,

а₂₁х₁ + а₂₂х₂ + ... + а_2nх_n = b₂,

 .............................................. (3)

а_m1х₁ + а_m2х₂+ ... + а_mnх_n = b_m,

где а_ij  числовые коэффициенты, b_i свободные члены, х_j  неизвестные, i = 1,…, m, j = 1,…, n.

Отличительная черта линейных систем в том, что к неизвестным применяются только линейные операции  алгебраическое сложение и умножение на число. Решением системы (3) называется упорядоченный набор значений неизвестных (х₁, х₂, ... , х_n), при подстановке которых в каждое уравнение получаются верные равенства. Система, имеющая хотя бы одно решение, называется совместной; система, не имеющая решений, называется несовместной; система, имеющая единственное решение, называется определенной; система, имеющая более одного решения, называется неопределенной. Если в системе (3) все свободные члены равны нулю, то она называется однородной. Системы, имеющие одинаковые множества решений называются равносильными. Для обозначения равносильныъх систем используются символы  или .

П ример 16.Какой набор чисел (1; 2; 7) или (3; 1; 0) является решением системы:

Решение. Нужно подставить каждую тройку чисел вместо x, y, z в эти уравнения:

1) 2)

Ответ: (1; -2; 7) не является решением, (3; 1; 0) является решением.

Системы двух уравнений с двумя неизвестными имеюи вид:

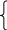 а₁₁х₁ + а₁₂х₂ = b₁,

а₂₁х₁ + а₂₂х₂ = b₂.

При решении такой системы можно использовать следующие формулы:

при условии, что .

Системы трех уравнений с тремя неизвестными имеют вид:

 а₁₁х₁ + а₁₂х₂ + а₁₃х₃ = b₁,

а₂₁х₁ + а₂₂х₂ + а₂₃х₃ = b₂,

а₃₁х₁ + а₃₂х₂ + а₃₃х₃ = b₃.

Методы решения таких систем рассматриваются ниже.

Для перехода к матричной записи вводятся обозначения:

А – матрица коэффициентов при неизвестных, Х – столбец неизвестных,

В – столбец свободных членов:

Тогда система (3) записывается в следующей матричной форме

Например, матричная запись системы трех уравнений с тремя неизвестными имеет вид:

§5. Методы решения систем

1. Сначала рассматривается метод Крамера для решения систем специального вида, когда число уравнений равно числу неизвестных, такие системы называются квадратными:

а ₁₁х₁ + а₁₂х₂ + ... + а_1nх_n = b₁,

а₂₁х₁ + а₂₂х₂ + ... + а_2nх_n = b₂,

 ........................................... (5)

а_n1х₁ + а_n2х₂ + ... + а_nnх_n = b_n.

Теорема Крамера. Пусть А – матрица коэффициентов в квадратной системе (5). Тогда:

1 ) если определитель А не равен нулю, то система (5) имеет единственное решение, которое находится по следующим формулам

где и _i  вспомогательные определители, получаемые из А путем замены i-го столбца на столбец В свободных членов:

_i = i = 1, ... , n;

2) если определитель А равен нулю и хотя бы один из _i отличен от

нуля, то система (5) не имеет решений;

3) если определитель А и все вспомогательные определители _i равны нулю, то система (5) имеет бесконечное множество решений.

Доказательство (см. [1. с. 163]).

x + 2y + z = 8,

Пример 17. Решить методом Крамера систему 3x + 2y + z = 10,

4x + 3y  2z = 4.

Решение. Сначала находится определитель = 14.

Так как А 0, то система имеет единственное решение, которое находится по формулам (6). Для этого находятся вспомогательные определители:

Тогда получается: х = 14:14 = 1; у = 28:14 = 2; z = 42:14 = 3.

Ответ: х = 1; у = 2; z = 3 .

2. Второй метод называется методом Гаусса. Он применяется к любым системам вида (3) и использует так называемые эквивалентные преобразования систем, которые, по определению, не изменяют множество решений системы. Такими преобразованиями являются:

а) перестановка уравнений;

б) умножение уравнения на число, отличное от нуля;

в) сложение уравнений.

С помощью этих преобразований система (3) приводится к так называемому виду трапеции:

а₁₁^*х₁ + а₁₂^*х₂ + ... + а_1k^*х_k+ ... + а_1n^*х_n = b₁^*,

а₂₂^*х₂ + ... + а_2k^*х_k+ ... + а_2n^*х_n = b₂^*,

 ….......................................... (7)

а_mk^*х_k + ... + а_mn^*х_n = b_m^*.

Здесь b_i^*, a_ij^*- уже другие числа, полученные в результате указанных преобразований, но эта система равносильна исходной системе (3).

Если в полученной системе (7) число уравнений равно числу неизвестных, то она называется треугольным видом исходной системы. В ходе преобразований уравнений системы могут возникать равенства следующих видов:

1) 0 = 0, (такое равенство отбрасывается, при этом число уравнений уменьшается);

2) 0 = b, где b  0, (в этом случае говорят, что получено противоречие и потому система не имеет решений).

Теорема Гаусса. Пусть система (3) эквивалентными преобразованиями приведена к виду (7). Тогда:

1) если в (7) нет противоречий и число уравнений равно числу неизвестных, то система (3) имеет единственное решение;

2) если (7) содержит противоречие, то система (3) не имеет решений;

3) если в (7) нет противоречий, но число уравнений меньше числа неизвестных, то система (3) имеет бесконечное множество решений.

Доказательство (см. [1. с. 169]).

Метод Гаусса наиболее важен для практики и по сравнению с другими методами имеет следующие достоинства:

1) он менее трудоемкий, позволяет легко установить, является ли данная система совместной или несовместной;

2) в случае совместности системы он позволяет легко определить, является ли данная система определенной или неопределенной;

3) в случае определенной системы, ее единственное решение вычисляется с помощью несложной процедуры, (см. пример 18);

4) в случае неопределенной системы он позволяет легко построить так называемые базисные решения, с помощью которых описывается множество всех решений данной системы, (см. ниже §6).

3x + 2y + z = 10,

Пример 18. Решить методом Гаусса систему x + 2y + z = 8,

x + 3y 2z = 4.

Решение. 1-й шаг. На первое место переставляется уравнение, в котором коэффициент при первой неизвестной х не равен 0 и является наиболее удобным для дальнейших преобразований. Здесь во 2-м уравнении коэффициент при х равен 1, поэтому меняются местами 1-е и 2-е уравнения:

x + 2y + z = 8,

3x + 2y + z = 10,

x + 3y 2z = 4.

2-й шаг. 1-е уравнение умножается на 3 и прибавляется ко 2-му уравнению, затем опять 1-е уравнение умножается на  и прибавляется к 3-му уравнению, получается равносильная система

 хyz

yz

yz.

3-й шаг. 2-е уравнение умножается на 5, 3-е уравнение умножается на 4, и получается равносильная система:

 хy z

yz

yz.

4-й шаг. К 3-му уравнению прибавляется 2-е уравнение и получается система в треугольном виде:

 хy z

 yz 

  z.

5-й шаг. Полученная система не содержит противоречий, и в ней число уравнений равно числу неизвестных. Следовательно, исходная система имеет единственное решение, которое находится следующим образом. Из 3-го уравнения находится значение для z: z = 42:(14) = 3. Это значение подставляется во 2-е уравнение и находится значение для у: у = ( 103):20 = 2. Далее, найденные значения z = 3, у = 2 подставляются в 1-е уравнение, и находится значение х: х = 8  22  3 = 1.

Ответ: х = 1, у = 2, z = 3.

Другие из указанных выше достоинств этого метода будут рассмотрены в следующем параграфе.

Иногда метод Гаусса описывают с использованием матричной записи (4) данной системы. При этом вместо уравнений производят преобразование так называемой расширенной матрицы:

А* = (8)

Допускаются следующие три преобразования: а) перестановка строк, б) умножение строк на число, отличное от нуля, в) сложение строк. С помощью этих преобразований расширенная матрица приводится к виду трапеции:

(9)

По этой матрице восстанавливается система (7) и производятся указанные выше действия.

3. Третий метод матричный, он применяется к квадратным системам вида (5), использует их матричную форму записи (4) и основан на следующих рассуждениях. Пусть АХ = В – матричная форма системы (5), при этом матрица А имеет обратную матрицу А^1. При умножении слева обеих частей данного матричного равенства на обратную матрицу получается равенство: А^1(АХ) =А^1В. Отсюда, согласно матричным свойствам 7, 8 и соотношению (1), последовательно получаются равенства:

(А^1А)Х = А^1В, Е_nХ = А^1В, Х = А^1В

Последнее равенство Х = А^1В есть матричная записьрешения системы.

x + 2y + z = 8,

Пример 19. Решить систему уравнений 3x + 2y + z = 10,

x + 3y 2z = 4,

с помощью обратной матрицы.

Решение. Сначала вводятся следующие обозначения:

Тогда система запишется в виде: АХ = В, ее решение имеет вид Х = А^1В.

Н аходится обратная матрица А^1. Определитель А=14 был найден в примере 3, тогда находятся алгебраические дополнения и применяется формула (2).

Ответ: x = 1, y = 2, z = 3.

Системы линейных уравнений возникают при решении многих задач линейного программирования, которые имеют большое практическое применение. В следующем примере рассматривается наиболее простая задача такого вида.

Пример 20. В производстве трех типов продукции используются три вида сырья А, В, С . Нормы затрат сырья на производство единицы каждого типов продукции и запасы сырья даны в следующей таблице.

Тип продукции Вид сырья	Нормы затрат			Запасы
	1-й тип	2-й тип	3-й тип
А	2	3	1	245
В	1	0	2	130
С	3	4	0	270

Требуется определить план производства, обеспечивающий использование всего сырья.

Решение. Пусть х₁, х₂, х₃  количество единиц продукции 1-го, 2-го, 3-го типов соответственно, которое должно выпустить предприятие. Тогда расход сырья А равен произведению количества единиц каждого типа продукции на соответствующие нормы затрат этого сырья: 2х₁ + 3х₂ + х₃ . Это должно равняться его запасам 245, получается первое уравнение: 2х₁ + 3х₂ + х₃ = 245. Аналогично получаются уравнения для сырья В и С, и задача сведена к решению следующей системы линейных уравнений:

2х₁ + 3х₂ + х₃ = 245,

х₁ + 2х₃ = 130,

3х₁ + 4х₂ = 270.

Решение этой системы находится методом Гаусса.

1 -й шаг. Переставляются местами х₁ + 2х₃ = 130,

1-е и 2-е уравнения 2х₁ + 3х₂ + х₃ = 245, 3х₁ + 4х₂ = 270.

2 -й шаг. 1-е уравнение умножается х₁ + 2х₃ = 130,

на2 и прибавляется ко 2-у  3х₂  3х₃ = 15,

уравнению  3х₁ + 4х₂ = 270.

3 -й шаг. 1-е уравнение умножается  х₁ + 2х₃ = 130,

на 3 и прибавляется к 3-у  3х₂ 3х₃ = 15,

уравнению 4х₂  6х₃ = 120.

4 -й шаг. 2-е уравнение умножается х₁ + 2х₃ = 130,

на4/3 и прибавляется к 3-у 3х₂ 3х₃ = 15,

уравнению 2х₃ = 100.

5-й шаг. Получилась равносильная система в треугольном виде. Тогда из 3-го уравнения находится значение х₃ = (100):(2)=50; из 2-го уравнения находится значение х₂ = (15+350):3 = 45; из 1-го уравнения находится значение х₁ = 130 250 = 30 .

Ответ: план выпуска равен 30, 45 и 50 единиц продукции.