Глава 3. Элементы дискретной математики

Дискретная математика – это область математики, занимающаяся изучением свойств структур конечного характера. Главная ее особенность заключается в отказе от таких понятий, как предел, непрерывность, производная и интеграл. В связи с этим многие сильные средства классической математики, как правило, становятся мало приемлемыми в дискретной математике. В данном разделе рассматриваются основные понятия теории множеств, математической логики, комбинаторики и теории графов.

§1. Основные понятия теории множеств

По­нятие множество широко используется в современной математике и служит основой построения остальных математических понятий. Но, тем не менее, стро­гое определение множества не возможно, поэтому говорят, что множество  это первичное понятие, и вместо определения обычно дают лишь описание этого понятия. Множество  это совокупность некоторых объ­ектов, объединенных по какому-нибудь признаку. При этом, считают, что произвольный объект либо принадлежит данному множеству, либо не принадлежит. Объекты, принадлежащие множеству, называются его элементами. Множества принято обозначать заглавными буквами, например: А, В, Q, N, R, а элементы множеств обозначаются малыми буквами: a, b, х, у , z, t. Если объект х принадлежит множеству А, то пишут хА; если же х не принадлежит А, то пишут х.

Вторая важная особенность понятия множества в том, что множество само является единым объектом и может входить в другие множества.

Пример 1. а). Совокупность студентов некоторой группы университета является множеством. Действительно имеется список студентов этой группы и можно определить, кто принадлежит, и кто не принадлежит этому множеству. Кроме того, группа рассматривается как единый объект и, например, она принадлежит множеству всех студенческих групп университета.

б). Множество красивых девушек в данной студенческой группе. Здесь свойство "быть красивой девушкой" является нечетким понятием, и, быть может, не всегда можно определить, какие студентки принадлежат этому множеству и какие ему не принадлежат. В таком случае говорят, что это нечеткое множество, и в обычном курсе математики такие множества не рассматривается. Дело в том, что для рассмотрения нечетких понятий традиционная математическая логика просто не применима. И очень похоже, что попытка теоретизирования в рамках этой логики, например, на моральные темы, должна приводить к ложным результатам. Вероятно, что рассуждать о таких вещах в принципе возможно, но это надо делать в какой-то другой логике. Тем не ме­нее, люди как-то ухитряются обсуждать между собой различные вопросы, связанные с нечеткими понятиями, и при этом им удается как-то друг друга понимать.

Множество, не имеющее элементов, называется пустым и обо­значается символом . Множество, состоящее из одного объекта а, называется одноэле­ментным, обозначение: {а}. Конечное множество, состоящее из элементов х_1, х₂, ... , х_n, обозначается записью этих элементов в фигурных скобках: {х₁, х₂, ... , х_n}. Бесконечные множества задаются с помощью характеристических свойств элементов. Например, если формула Р(х) описывает свойство, характеризующее элементы множества А, то А обозначается записью {x / Р(х)}.

В математике рассматриваются следующие числовые множества. Натуральные числа - это целые по­ложительные числа 1, 2, 3, ... , их множество обозна­чается буквой N или записью {1, 2, ..., n, ...}. Множество всех целых чисел обозначается буквой Z или через {0, 1, 2, ..., n, ...}. Натуральное число, делящееся без остатка на 2, называется четным; множество таких чисел обозначается {2n / nN }. Остальные натуральные числа называются нечетными, и их множество обозначается {2n 1 / nN }. Натуральное число, делящееся без остатка на число k, называется кратным k, множество всех таких чисел обозначается { k n / nN }.

Рациональные числа – это все целые числа и дробные числа вида , где m, n - целые числа и n  0; множество таких чисел обозначается буквой Q и записью вида: . Еще рассматриваются числа, являющиеся бесконечными непериодическими десятичными дробями: m  0,c₁c₂c₃ … .

Т акие числа называются иррациональными, они задаются приближенно. Например,

Множество иррациональных чисел обозначается буквой I. Рациональные и иррациональные числа называются вещественными числами, их множество обозначается буквой R.

Пусть а, b  вещественные числа. Множество всех ве­щественных чисел х, удовлетворяющих неравенствам: а < x и х < b, называется ин­тервалом и обозначается записью (а; b). Множество, состоящее из интервала (а; b) и его концов, называется сегментом или замкнутым промежутком, и обозна­чается через [а; b]. Наглядно эти множества изображаются на числовой оси в виде:

a b a b

( ) [ ]

Черт. 15.

Рассматриваются также полусегменты вида [а; b) = хR : а  х  b, (а; b = хR : а  х  b, и неограниченные множества вид (; b), (а; +), а; +), (; b, (; +).

Если все элементы множества А являются элементами множества В, то говорят, что А включено в В или А подмножество В, обозначение: А  В.

Два множества А и В называются рав­ными, если они состоят из одних и тех же элементов, обозначение: А = В; в противном случае пишут А  В.

Например: а) N  Q  R ; б) [0; 1]  [0; 2]; в) [2; 1]  (; 2);

д) {1, 1} = {1}; е) {1, 2}  {{1}, {2}}; ж)   {0}; з)   {}.

Введенные отношения обладают следующими свойствами:

1) А = А и А  А; 2) если А = В и В = С, то А = С;

3)   А; 4) Если А  В и В  С, то А  С;

5) А = В тогда и только тогда, когда А  В и В  А.

Объединением (или суммой) множеств А и В называется множество, со­стоящее из всех элементов, принадлежащих хотя бы одному из этих множеств А, В (обозначение: АВ). Это определение выражают формулой

АВ = {x / xA или xB }.

Пересечением множеств А и В называется множество, состоящее из всех элементов, принадлежащих одновременно обоим множествам А и В (обозначение: АВ). Это определение выражают формулой

АВ = {x / xA и xB }.

Разностью множеств А и В называется множество, состоящее из всех тех элементов множества А, которые не принадлежат множеству В (обозначение: А\В или АВ). Это определение выражают формулой

А\В = {x / xA и xB }.

Наглядно введенные операции над множествами изображают диаграммами Венна (или кругами Эйлера), приведенными на чертеже 16, а)  в).

АВ AB

АВ

А\В



а) Объединение б) Пересечение в) Разность г) Дополнение

Черт. 16.

В конкретных исследованиях или рассуждениях обычно рассматриваются объекты специального вида. Например, в арифметике рассматриваются только целые числа, в математическом анализе - вещественные числа, в планиметрии – точки, линии и фигуры на плоскости. В таких случаях вводят универсальное множество или универсум, которое состоит из всех рассматриваемых объектов (обозначение: U). В предыдущих примерах универсальными множествами являются, соответственно, Z, R и все точки плоскости. На диаграммых Венна универсум изображается внешним прямоугольником.

Если универсальное множество U задано, то в дальнейшем рассматривают только его подмножества. В этом случае определяется еще одна операция  взятие дополнения. Дополнением множества А называется множество, состоящее из всех тех элементов U, которые не при­надлежат А (обозначение:А ). Это определение выражается формулами

А = U \ А или А = { xU / xA }.

(См. также чертеж 16 г).).

Раздел, в котором изучаются множества, называется теорией множеств. При строгом изложении вводится формальный язык этой теории и все определения и утверждения формулируются в этом языке. Но в данном курсе теория множеств имеет лишь вспомогательное значение и поэтому определяемые здесь понятия и формулируемые утверждения не являются строгими и носят ознакомительный характер.

Следующие равенства выражают основные свойства данных операций (справа указаны названия этих свойств).

Теорема 1. Для любых подмножеств А, В, С некоторого универсального множества U выполняются следующие равенства:

1. АВ = ВА; 1. АВ = ВА. (коммутативность)

2. (АВ)С = А(ВС); 2. (АВ)С = А(ВС). (ассоциативность)

3. А(ВС) = (АВ)АС);

3. А(ВС) = (АВ)АС). (дистрибутивность)

4. (АВ)A = А; 4. (АВ)A = .А (законы поглощения)

  (законы де Моргана)

6. АА = А; 6. АА = А. (идемпотентность)

(закон двойного дополнения)

8. А А = ;  8. А А = U.

9. UА = А; 9. А = А.

10. А = ; 10. UА= U.

11.U = ; 11.= U.

Эти равенства (кроме 7) объединены в пары: 1 и 1, 2 и 2, и т. д. Цель такого объединения в том, чтобы продемонстрировать так называемый закон двойственности. Равенство теории множеств, полученное из другого равенства заменой всех вхождений  на ,  на , U на ,  на U, называется двойственным исходному равенству. Указанный закон двойственности утверждает, что если некоторое равенство является верным, то и двойственное ему равенство так же верно.

В связи с этим законом, можно представить следующую фантастическую ситуацию. Некий студент-заочник Заумкин Иван, изучая законы теории множеств, перепутал значения символов , , U, . Он считал, что  и  обозначают соответственно объединение и пересечение множеств, а символы U и  обозначают соответственно пустое и универсальное множества. Тем не менее, на экзамене этот студент, используя равенства теоремы 1, правильно выполнил все задания на преобразование формул, содержащие эти символы.

Применение равенств теоремы 1 основано на следующем утверждении.

Теорема 2 (о замене равных множеств). Пусть в формуле F, определяющей некоторое множество, встречается множество А, и формула F^* получается из F заменой А на множество В. Тогда если А = В, то формулы F и F^* определяют равные множества.

Доказательство осуществляется индукцией по логической глубине формулы F. (см.[3] , с.47-61).

Пример 2. Упростить теоретико-множественные формулы:

Решение. а). Используются тождества 5, 7, 2, 6 теоремы 1:

б). Используются тождества 3, 8, 5, 9, 8 теоремы 1:

= =

= = = U.

Множества А, В называются непересекающимися, если АВ = . Множества А₁, А₂, …, А_к называются попарно непересекающимися, если любые два из них непересекающиеся множества.

Пусть А  конечное множество, и n(A)  число элементов этого множества. Тогда верны следующие формулы.

Теорема 3. Пусть множества А, В, С  конечные, тогда:

а) если А, В, С попарно непересекающиеся множества, то

n(AВС) = n(A) + n(В)  n(С);

б) если А, В, С произвольные множества, то

n(AВ) = n(A) + n(В)  n(AВ) и

n(AВС) = n(A)+n(В)n(С)n(AВ)n(AС)n(ВС)+n(AВС).

Пример 3. Из 20 человек двое изучали только английский язык, трое – только немецкий, шестеро – только французский. Никто не изучал трех языков. Один изучал немецкий и английский, трое – французский и английский. Сколько человек изучало французский и немецкий языки?

Решение. Пусть А, В, С обозначаютмножества человек, изучавших

соответственно английский, немецкий, французский языки, и А', В', С' - множества человек, изучавших соответственно только английский, только немецкий, только французский языки. По условию n(А') = 2, n(B') = 3, n(C') = 6, n(АВС) = 0, n(АВ) = 1, n(АС) = 3, и требуется определить n(ВС). Универсальное множество U образуют 20 человек: n(U) = 20. На чертеже 17 с помощью диаграммы Венна изображены его основные части и количество элементов в них, кроме n(ВС) = х.

А' АВ В'

1

2 3 0 3 х

АС 6 ВС С'

Черт. 17.

Так как эти части непересекающиеся, то, по теореме 3а), n(U) = n(А') + n(B') + n(C') + n(АВ) + n(АС) + n(ВС) + n(АВС). Отсюда следует, что n(ВС) =  = 5. Значит, французский и немецкий языки изучали 5 человек.

Пример 4. В классе 30 учеников. Все, кроме двух, имеют оценки «5», «4» и «3». Число учащихся, имеющих оценки «5» – двенадцать, «4» – четырнадцать, «3» – шестнадцать. Трое учатся лишь на «5» и «4», трое – лишь на «5» и «3» и четверо  лишь на «4» и «3». Сколько учащихся имеют одновременно оценки «5», «4» и «3»?

Решение. Пусть буквы А, В, С обозначают множества учеников, которые имеют соответственно оценки "5", "4", "3". По условию число элементов в этих множествах известно: n(A) = 12, n(В) = 14, n(С) = 16. Пусть х  число учащихся, имеющих одновременно оценки «5», «4» и «3», т.е. n(AВС) = х. Множество AВ состоит из учащихся, которые учатся только на «5» и «4», или на «5», «4» и «3». Следовательно, n(AВ) = 3+ х. Аналогично получаются равенства: n(AС) = 3+х, n(ВС) = 4+х. Еще по условию на "5", "4"или "3" учатся 28 человек, поэтому n(AВС) = 28. Найденные значения нужно подставить в формулу для n(AВС) из теоремы 3б), получится уравнение: 28 = 12+1416(3+х)(3+ х)(4+х)+х. Отсюда следует, что х = 2.

Пример 5. Пусть А состоит из натуральных делителей числа 45, В  из натуральных делителей числа 60. Найти множества:

а) АВ; б) АВ; в) А \ В; г) В \ А.

Решение. По условию А состоит из натуральных чисел, которые делят 45 без остатка, тогда А = {1, 3, 5, 9, 15, 45}. Аналогично, В = {1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60}. а) Множество АВ состоит из чисел, принадлежащих А или В, поэтому АВ = {1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 20, 30, 45, 60}. б). Множество АВ состоит из чисел, принадлежащих одновременно А и В, поэтому АВ = {1, 3, 5, 9, 15}. в). Множество А \ В состоит из чисел, принадлежащих А и не принадлежащих В, поэтому А \ В = {9, 45}. г). Множество В \ А состоит из чисел, принадлежащих В и не принадлежащих А, поэтому В \ А = {2, 4, 6, 10, 12, 20, 30, 60}.

Пример 6. Пусть множество А состоит из натуральных чисел, кратных 3, В  из натуральных чисел, кратных 6, С  из натуральных чисел, кратных 5. Записать эти множества и множества АВ, АC, BC, АВC символически.

Решение. По определению, А = {3n / nN}, B = {6n / nN}, C = {5n / nN}. Множество АВ состоит из чисел, принадлежащих одновременно А и В. Но числа кратные 6 можно записать в виде 3(2n), поэтому они также являются кратными 3. Следовательно, ВА и тогда АВ = В = {6n / nN}. Множество АС состоит из чисел, принадлежащих А и С, тогда такие числа должны делится одновременно на 3 и 5. Следовательно, АС состоит из чисел, кратных 15, поэтому АС = {15n / nN}. Аналогично показывается, что ВС = {30n / nN} и АВC = {30n / nN}.

Пример 7. Пусть А = ( ; 6], B= [2; 7], C = [3; +). Изобразите на чертеже эти множества и найдите: а) А \В; б) (А В) \ С; в) (ВС) \ А.

Решение. На чертеже 18 данные множества изображены на параллельных числовых осях с одинаковым масштабом и синхронно.

A А

 ///////////////////////////////////////] 

0 1 2 3 4 5 6 7 8

В B В

  [/////////////////////////] 

0 1 2 3 4 5 6 7 8

C

 [///////////////////////////////////////////

0 1 2 3 4 5 6 7 8

Черт. 18.

а). Множество В состоит из точек, не принадлежащих В, поэтому В = (; 2)(7; +). Теперь нужно из множества А удалить точки этого множества, получится сегмент [2; 6], поэтому А \В = [2; 6].

б). МножествоА состоит из точек, не принадлежащих А, поэтому А = (6; +). Множество В указано в пункте а). Множество (А В) состоит из точек, принадлежащих А иВ , следовательно: (А В) = (7; +). Этот интервал входит в множество С, поэтому (А В) \ С = .

в). Множество (ВС) состоит из точек, принадлежащих В или С , следовательно: (ВС) = [2; +). Из этого множества нужно удалить точки, принадлежащие А, получится интервал (6; +) , т. е. (ВС) \ А = (6; +).

При построении множеств, описываемых с помощью числовых неравенств, применяется следующий метод интервалов.

Основной случай. Все члены неравенства переносятся в левую часть, полученное выражение разлагается на множители и преобразуется к виду:

i). а(х  х₁) (х – х₂) … (х – х_n) > 0, или ii). а(х  х₁) (х – х₂) … (х – х_n)  0.

Полученные числа х₁, х₂, … , х_n отмечаются на числовой оси и строятся соответствующие интервалы, затем определяются знаки интервалов. Для этого в крайнем правом интервале выбирается произвольная точка х₀ и вычисляется значение левой части неравенства в этой точке. Если это значение положительное, то в правом интервале ставится знак +, а если оно отрицательное, то ставится знак , в остальных интервалах знаки чередуются. Теперь, искомое множество равно объединению всех интервалов, имеющих знак +, если рассматривается неравенство вида i); а в случае неравенства вида ii) искомое множество равно объединению всех интервалов, имеющих знак + вместе с концами этих интервалов.

Остальные виды неравенств сводятся к данному основному случаю.

Пример 8. Построить интервалы изменения переменного х, удовлетворяющего неравенствам:

1). (х 1)(х 2)  0; 2). (х 3)(5  х) > 0; 3). х² + 3х  4  0.

Решение. Применяется метод интервалов. 1). Исходное неравенство умножается на (1), получится неравенство вида (х1)(х2)  0. Числа 1, 2 отмечаются на числовой оси, получается три интервала (см. чертеж 19).

 +

 1 2 

Черт. 19.

Затем, в правом интервале берется число 3 и вычисляется значение левой части последнего преобразованного неравенства: (31)(32) = 2 < 0. Получено отрицательное число, следовательно, в правом интервале ставится , а в остальных интервалах знаки чередуются. Здесь рассматривается неравенство вида ii), поэтому искомое множество равно интервалу со знаком +, включая концы этого интервала, т.е. оно равно сегменту 1; 2.

2). (х 3)(5  х) > 0. Здесь чтобы получить основной случай, нужно во второй скобке вынести знак – за скобку, получится: (х3)(х5)>0. Теперь, так же как в пункте 1), строятся интервалы и определяются их знаки, см. чертеж 20.

 

 3 5 

Черт. 20.

Преобразованное неравенство имеет вид i), поэтому искомое множество равно (3; 5).

3 ). х² + 3х  4  0. Здесь левая часть является квадратным трехчленом вида: ax² + bx + c , который сводится к виду а(х  х₁) (х – х₂), где х₁, х₂ – его корни. Для вычисления этих корней используется формула:

Получается: х₁ = 1, х₂ = 4, и исходное неравенство преобразуется к виду: (х  1) (х + 4)  0. Так же как пункте 1) строятся интервалы и определяются их знаки, см. чертеж 20. Рассматриваемое неравенство преобразовано к виду ii), поэтому искомое множество равно (; 4]1; +).

 

 4 1 

Черт. 21.

Пример 9. Пусть А и В  множества точек М(х, у) плоскости, координаты которых удовлетворяют неравенствам 5х + 3у  15, 3х  2у  6, соответственно. Изобразите множество АВС, где С  множество точек М(х, у), координаты которых удовлетворяют неравенствам х  0, у  0.

Решение. 1). Построение множества А. Сначала строится граница, задаваемая уравнением 5х + 3у = 15. Это прямая линия, для ее построения составляется таблица, в которой вычисляются координаты двух точек, лежащих на прямой.

х	0	3
у	5	0

Таким образом, прямая проходит через две точки С(0; 5), D(3; 0) и разбивает плоскость на две части, одна из которых образует множество А. Чтобы выбрать нужную полуплоскость, берется вспомогательная точка, например, О(0; 0), и ее координаты подставляют в первое неравенство: 50 + 30  15.

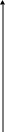
Y

5 С

G

О F D X

2 3

3 Е

Черт. 22.

Получилось верное неравенство, тогда выбирают полуплоскость, содержащую точку О(0; 0), искомое множество А состоит из всех точек плоскости, лежащих на прямой CD и левее ее.

2). Построение множества В. Так же как в пункте 1) сначала строится граница, задаваемая уравнением 3х  2у = 6:

х	0	2
у	3	0

Это прямая линия, проходящая через точки E(0; -3), F(2; 0), Пусть О(0; 0) - вспомогательная точка, ее координаты подставляют во второе неравенство: 30  20  6. Получилось верное неравенство, тогда множество А состоит из всех точек плоскости, лежащих на прямой EF и левее ее.

3). Построение множества С. Неравенства х  0, у  0 задают первую координатную четверть.

Искомое множество АВС  это множество точек, лежащих внутри четырехугольника ОСGF и на его сторонах, (см. чертеж 22). Чтобы проверить ответ, можно взять любую точку внутри этого четырехугольника, например, (1; 1) и подставить ее координаты в исходные неравенства: 51 + 31  15; 31  21  6; 1  0; 1  0. Все неравенства верные, значит, решение верное.