Тема 3. Нелинейности при тепло- и массообмене

1. Учет зависимости коэффициента теплопроводности от температуры

Типичной нелинейностью при решении задач теплопроводности является зависимость коэффициента теплопроводности от температуры, которая слабо проявляется для сред металлических, но весьма заметна для сред неметаллических, т.е.

 = (Т).

В этом случае уравнение теплопроводности принимает вид:

ρС_v · (дТ/дt) = д/дх(λ(Т)дТ/дх) . (1)

Для учета нелинейности подобного рода вводится искусственная функция (х,t), определяемая как

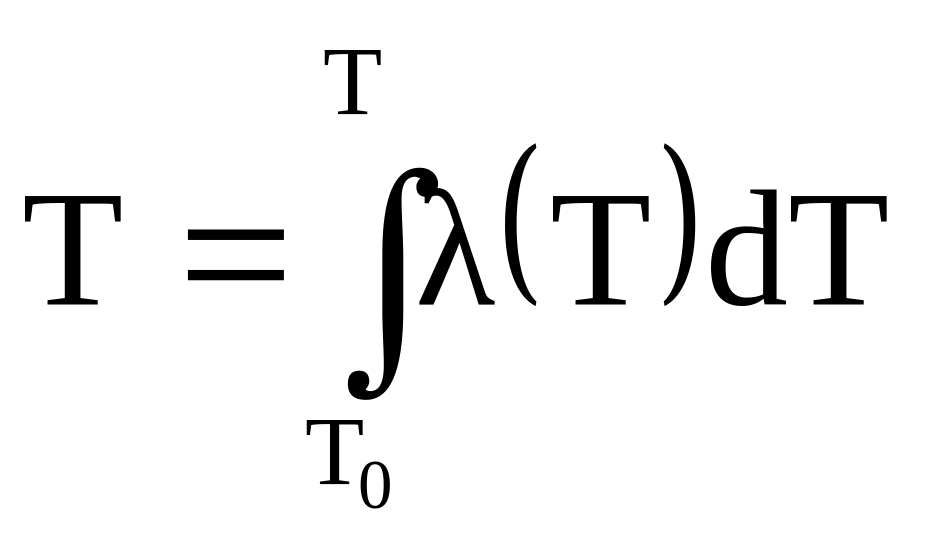, (2)

где отсчет температуры Т₀ в шкале температур выбирается произвольно, исходя из удобства решения конкретной задачи. В результате уравнение (1) преобразуется к виду в установившемся режиме (дТ/дТ)=0

. (3)

Граничные условия 1-го рода для функции  сохраняются, в условиях 2-го и 3-го рода члены λ заменяются на . Соответствие между температурой Т и функцией  однозначно определяется зависимостью (2). В частности граничные условия 3-го рода принимают вид

(4)

3.2. Конечно-разностная аппроксимация дифференциальных уравнений и граничных условий

Многие задачи, описываемые уравнениями (3) и (4), аналитически не решаются. Поэтому применяются приближенные методы. Одним из таких методов является метод конечно-разностной аппроксимации. Предположим ищется решение (3) на интервале х = [0;1]. Этот интервал разбивается на n частей х и в каждой i точке узле интервала производная д/дх записывается как д/дх  (_i+1 - _i)/x. Применяя подобное приближение ко 2^-й производной и (3), получаем

или

. (5)

На границах интервала (i = 0, i = n) условия приобретают вид

Т_i или _i – задано (граничные условия 1-го рода),

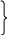 _i+1 - _i = Q (х_i) x при i = 0 или = Q (х_i) x при i = n

(граничные условия 2-го рода), (6)

_i+1 - _i + α(Т(Ф_i) –Т₀ при i = 0 или Ф_i – Ф_i-₁ + α(Т(Ф_i) –Т₀ при i = n

(граничные условия 3-го рода (4)).

В результате дифференциальное уравнение (3) и соответствующие граничные условия заменяются системой из n линейных конечно-разностных алгебраических уравнений, которые решаются известными методами.

3.3. Итерационные методы решения конечно-разностных уравнений

Уравнения (5) и (6) решаются методом последовательных приближений. В начале задается так называемое начальное распределение, выбираемое произвольно. Затем по (5) и (6) в каждом i узле интервала последовательно рассчитываются новые значения функции _i. После обсчета всех узлов новое решение принимается за начальное и процесс расчета новых значений функций продолжается. Указанный процесс носит название итерационного. Итерации заканчиваются тогда, когда новые значения функции в итерации отличаются от значений функции в предыдущей итерации на удовлетворяющую нас погрешность.

Аналогичные методы используются также при решении задач, описываемых уравнениями массообмена.