Коэффициент роста или снижения показывает, во сколько раз увеличивается или уменьшается данный уровень ряда по сравнению с уровнем, принятым за базу сравнения. В зависимости от базы сравнения коэффициенты роста или снижения могут быть также цепными (1) и базисными (2):

Между цепным и базисным коэффициентами роста существует определенная взаимосвязь. Если динамические ряды приведены за один и тот же период времени, тогда произведение цепных индексов или коэффициентов роста равно соответствующему базисному индексу или коэффициенту роста. Если же разделить последний базисный индекс или коэффициент роста на предыдущий, то в результате получится соответствующий цепной индекс или коэффициент роста.

6. Коэффициент прироста показывает, на сколько относительных единиц увеличивается или уменьшается уровень ряда по сравнению уровнем, принятым за базу сравнения. В самом общем виде коэффициент прироста рассчитывается как (5), формула для цепного коэффициента прироста имеет вид (5а), а для базисных (5б):

7. Темп роста или снижения Т показывает, сколько % сравнительный уровень составляет по отношению к другому уровню, принятому за базу сравнения, и численно равен коэффициенту роста, выраженному в процентах:

Для цепных формула (6) имеет вид (6а), для базисных (6б)

8. Темпы прироста показывают на сколько процентов увеличивается или уменьшается данный уровень ряда по сравнению с уровнем, принятым за базу сравнения и вычисляется по формулам:

Средние величины в рядах динамики.

9. Средний коэффициент роста показывает, во сколько раз увеличился или уменьшился данный уровень ряда по сравнению с уровнем, принятым за базу сравнения в течение целого периода времени, однако взятый в расчете на единицу n-го периода. Например, это может быть средний дневной коэффициент роста показателя в течение недели, либо средний еженедельный коэффициент роста в течение месяца, либо ежемесячный коэффициент роста в течение года. Пусть нам даны:

t₀ t₁ t₂ t₃…t_n

y₀ y₁ y₂ y₃…y_n

Следовательно средние величины коэффициентов роста могут быть рассчитаны с использованием ряда альтернативных формул, представляющих собой модификации формул средней геометрической в зависимости от того, какие имеются исходные данные. Пусть, например, мы имеем цепные коэффициенты роста к₁, к₂, к₃…к_n – следовательно их средняя величина может быть определена по формуле (8)

В формуле (8) n – число коэффициентов роста за отдельные единицы времени. Если в (8) подставить расчетные формулы, по которым были рассчитаны цепные коэффициенты роста, то (8) принимает вид (8а)

, где y_n – конечный уровень ряда

y₀ – начальный уровень ряда

n – число периодов времени составивших целый период, для

n –го исчисления коэффициента прироста.

Поскольку в (8а) подкоренное выражение – базисный период, то (8а) можно представить, как (8б)

10. Средний коэффициент прироста показывает, на сколько относительных единиц в среднем увеличивается или уменьшается данный уровень ряда по сравнению с принятым за базу сравнения в течение целого периода, взятый в расчете на единицу времени (9)

11. Средний темп роста . Его численная величина показывает, сколько процентов в среднем данный уровень ряда составил по отношению к базисному в единицу времени в течение всего составляющего периода (10)

12. Средний темп прироста показывает, на сколько увеличивается или уменьшается данный уровень ряда в единицу времени в среднем по сравнению с базисным в течение целого составляющего периода времени (11)

13. Абсолютное значение одного процента относительного прироста (y_1%) вычисляется по двум альтернативным формулам (12а) и (12б)

, y_баз – базисный уровень данного показателя, для которого рассчитывается его числовая величина.

Общие приемы и математические методы изучения и измерения связей общественных явлений. Корреляционный анализ и сущность корреалиционной связи.

Существуют два типа зависимости между общественными явлениями:

1. Корреляционная

2. Функциональная

При корреляционной связи определенному изменению одного явления соответствует в отдельных случаях различные по величине и направлению изменения другого явления.

Корреаляционная связь существует напрямую между уровнем квалификации и размером заработной платы работников, между величиной мощности заводского оборудования и объемом продукции предприятия, а также в бесчисленном множестве случаев.

При функциональной связи изменению одного явления соответствует строго определенные изменения другого явления, находящегося с ним в причинно-следственной связи.

При корреляционной связи изменению одного явления соответствует различные по величине и направлению изменения другого явления.

В теории статистики различают следующие виды признаков, корреляционная связь между которыми является предметом изучения:

1. Факториальные – признаки или факторы, обуславливающие изменение других признаков

2. Результативные или признаки результата – изменяющиеся под воздействием факториальных признаков.

Задачи статистики при исследовании корреалиционной связи между изучаемыми явлениями:

• выявление наличия корреляционной связи

• измерение (количественное выражени) степени тесноты корреалиционной связи между признаками

Корреляционная связь обнаруживается более ясно только при рассмотрении средних значений результативного признака, соответствующего средним значениям факториального признака. Благодаря исчислению групповых средних значений, влияние прочих причин взаимно погашаются и проявляются факториальные признаки. Поэтому основным методом выявления наличия корреалиционной связи является метод аналитических группировок и определение групповых средних. Сущность его состоит в том, что совокупность результатов разбивается на группы по величине факториального признака и для каждой группы вычисляются средние величины, как среднеарифметические результативного признака.

Для решения данной задачи с методом аналитических группировок и параллельно с ним применяется также графический метод. Главным образом для предварительного анализа и оценок предшествующих статистических характеристик или показателей. Графическое изображение результатов статистического наблюдения представляет собой корреляционное поле, т.е. точечный график, для построения которого на оси абсцисс откладываются значения факториально признака х, а по оси ординат – значения результативного признака у. Каждой единице изучаемой совокупности на графике соответствует одна точка, значение которой определяется величиной двух признаков, характеризующих эту единицу.

Пример: имеющиеся следующие данные, характеризующие результативность с/х производства в РК за 2003 год (таблица 4)

Таблица 4

Зависимость сбора зерна от размера посевных площадей зерновых культур за 2003г.

Для выявления корреалиционной связи между посевом зерновых и валовым сбором зерна для наглядности используют графический метод.

Зависимость сбора зерна от размера посевных площадей зерновых культур за 2003г (рисунок 1)

Рисунок 1

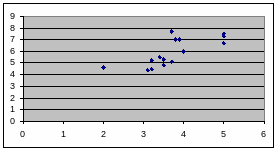
Точки не соединяются.

Задача №2

Корреляционная связь может быть прямая или положительная, когда увеличению одного явления соответствует увеличение значения другого явления. Обратная или отрицательная связь наблюдается тогда, когда увеличение одного явления вызывает уменьшение другого.

Если материалы статистического наблюдения были подвергнуты аналитической группировке, были вычислены средние, как среднеарифметическая, то эти средние в виде точек наносятся на график корреляционного поля. Соединив последовательно эти точки, мы получим так называемую эмпирическую линию регрессии, которая позволяет судить не только о наличии, но и форме корреляционной связи.

Линия корреляционной связи двух признаков фактора и результата отражает все изменения величины результативного признака, которые имели бы место при уравновешивании влияния всех других факторов, кроме признака фактора, называется теоретической линией регрессии.

Для нахождения параметров а и b необходимо решить систему параметрических уравнений следующего вида:

n – число параметрических данных х и у

Подставим полученные суммы в систему параметрических уравнений, определим величины a и b:

Построение на графике уравнения теоретической регрессии.

Измерение степени тесноты корреляционной связи. Для этого в статистике при прямолинейной форме зависимости используется коэффициент корреляции – r_xy, как частный случай коэффициента детерминации.

Коэффициент корреляции применяется потому, что в статистике при изучении корреляционной связи имеют дело не с приращением функции в связи с изменением аргумента, а с сопряжением вариацией результативного признака и факториального признака, при этом определение степени тесноты связи сводится к изучению этой сопряженности, т.е. того, в какой мере отклонение от среднего уровня одного признака сопряжено с другим, т.е. результативным признаком. Это означает, что при наличии полной прямой связи отклонение факториального признака должно обуславливать отклонение результативного признака. А при обратной связи отклонение последнего должно быть с противоположным знаком. Для расчета коэффициента корреляции предлагается использовать ряд формул, среди которых для данного примера рекомендуется выбрать следующую:

Коэффициент корреальности находится в пределах

Если значение коэффициента корреляции >0, наблюдается прямая корреляционная связь, если <0, то обратная корреляционная связь. В частном случае, если =0, корреляционная связь полностью отсутствует. В двух других случаях, если =+1(-1), корреляционная связь вырождается в функцию. В статистической практике, если коэффициент корреляции находится в пределах корреляционная связь практически отсутствует. Если наблюдается соотношение , то корреляционная связь считается слабой. При значениях корреляционная связь считается сильной.

Вычисленный коэффициент корреляции указывает на высокую степень тесноты между признаком-фактором и признаком-результатом, и говорят о том, что 7,42% вариации результативного признака обусловлено влиянием факториального признака и только 25,8% влиянием случайных причин, не зависящих от факториального признака, или в данном случае на 74,2% валовый сбор зерна обусловлен величиной посевных площадей.

При криволинейной зависимости между признаками значение коэффициент корреальности не применимо, т.к. оно недооценивает степень тесноты связи и в этом случае исчисляется коэффициент детерминации:

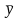- средняя арифметическая из фактических значений признака-результата в ряду распределения.

Коэффициент детерминации находится в следующих пределах:

(6)

Чем ближе значение коэффициента детерминации к 1, тем теснее связь между двумя признаками, или факториальный признак х оказывает большее влияние, чем результативный признак у.

Если же не наблюдается такого влияния, тогда вариация результативного признака, обусловленная влиянием факториального признака , т.е. числитель равен нулю и коэффициент детерминации тоже становится равным нулю, что указывает на полное отсутствие связи между двумя признаками.

Равенство коэффициента детерминации (1) говорит о вырождении корреляционной связи в функции:

Выравнивание рядов динамики с использованием метода намагниченных квадратов и аналитическое прогнозирование.

Сущность данного метода рассматривается на примере:

Следующие характеризуют производство с/х продукции в РФ за 1990-2001гг., млн. т (таблица 5)

Таблица 5

Шаг 1:

Выявление тенденции суммирования показателя производительности молока во времени графическим методом.

Шаг 2:

Нахождение количественной характеристики изменения показателя во времени. Для чего необходимо решить систему параметрических уравнений следующего вида:

где n – число параметрических данных

Для нахождения параметров a и b уровня прямой постоим параметрическую таблицу (таблица 6)

Таблица 6

Шаг 3:

Измерение степени тесноты связи между признаками, т.е. изменением производства молока во времени. Для прямой степень тесноты связи в частном случае характеризуется коэффициентом корреляции, в общем случае - коэффициентом детерминации.

что означает о наличии обратной связи факториального признака времени и результативного признака производительности молока, причем увеличение первого ведет к уменьшению второго.

4. Использование полученной модели для прогнозирования. Требуется рассчитать прогнозируемое значение результативного признака в 2002, 2003, 2004 годах.

5. Для расчета коэффициента детерминации определяем средние значения показателя производства молока:

Общие приемы и математические методы изучения и измерения общественных явлений. Выборочное наблюдение.

Выборочное наблюдение – это такое статистическое наблюдение, при котором отбор, подлежащих обследованию единиц изучаемого общественного явления организуется по принципу случайного отбора, в соответствии со схемами, рассматриваемыми в математической статистике и теории вероятностей, когда обследуется не вся совокупность, а лишь ее часть, обеспечивающая получение данных, характеризующих всю совокупность в целом. При случайном отборе каждая единица исследуюмого объекта получает равную вероятность попасть в количество обследуемых единиц и тем самым исключается субъективность, тенденциозность и односторонность в подборе таких единиц. При строгом соблюдении принятых правил отбора выборочное наблюдение адекватно отражает всю совокупность в целом, причем обследуется меньшее количество единиц, но полученные характеристики достаточно близко характеризуют состав наблюдательных единиц и всю массу единиц изучаемого объекта.

Примем следующие обозначения:

• N – число единиц во всей наблюдаемой совокупности, которая в данном случае носит название генеральной совокупности

• - генеральная средняя, т.е. среднеарифметическая для всей массы единиц генеральной совокупности

• М – абсолютное число единиц, обладающих данным признаком в генеральной совокупности

• W – относительная доля тех или иных единиц, обладающих данным признаком в генеральной совокупности, которая исходя из принятых обозначений может быть определена, как (1)

• - дисперсия признака в генеральной совокупности или генеральная дисперсия

• n – число единиц или объем выборочной совокупности

• - выборочная средняя или среднеарифметическая того или иного признака в выборочной совокупности

• m – число единиц, обладающих данным признаком выборочной совокупности

• - выборочная доля, т.е. относительное число единиц в общем объеме выборочной совокупности, обладающая данным признаком и исходя из принятых выше обозначений рассчитывается, как (2)

• - выборочная дисперсия или дисперсия, рассчитанная для выборочной совокупности.

Алгоритм определения выборочных характеристик.

Та часть единиц генеральной совокупности, которая непосредственно обследуется при выборочном наблюдении, представляет собой выборочную совокупность, а исчисляющиеся для этой части статистической характеристики носят название выборочные. При приближенном определении гипотетической среднеарифметической или другой генеральной характеристики или параметра в статистике используется следующий порядок:

1. По данным выборочного наблюдения вычисляется выборочная средняя или другой параметр

2. Задаются вероятностью Р того, что ошибка выборки не выйдет по абсолютной величине за определенные пределы. Это вероятность Р называется доверительной вероятностью, для которой чаще всего принимаются следующие значения:

Р=0,683

Р=0,954

Р=0,997

3. По физическим заимствованиям в математической статистике и теории вероятностей рассчитываются средние величины средних ошибок выборочной совокупности, и с их помощью определяются доверительные интервалы или пределы, т.е. минимальные и максимальные границы, в пределах которых с данной вероятностью Р предположительно находится генеральная средняя.

Ошибки выборочного наблюдения.

Для суждения о праве рассуждения выборочное наблюдение на всю генеральную совокупность определяют величину ошибок между сводными показателями выборочной и генеральной совокупности. Обычно сопоставляются следующие показатели:

• Предыдущая ошибка среднеарифметической , которая численно представляет собой следующее формульное выражение:

Откуда можно сделать вывод о том, в каких доверительных пределах находится генеральной средняя:

А также можно сделать вывод о том, что генеральная средняя может быть рассчитана:

• Предыдущая ошибка выборочной доли , которая по формальным признакам может быть выражена, как

Откуда

Из этого можно сделать вывод, что генеральная доля находится в следующих пределах:

Расчет предыдущей ошибки среднеарифметической, абсолютная величина данной ошибки рассчитывается как:

t – показатель кратности ошибки, зависящий от вероятности расчетов, который может гарантировать определенные размеры ошибки выборки.

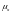- средняя ошибка среднеарифметической для выборочной совокупности, которая, например, для т.н. собственно случайного безповторного отбора, рассчитывается:

Коэффициент кратности t находится по специальным таблицам, приводимым во всех учебниках по математической статистике и теории вероятностей и общей теории статистики, а наиболее употребляемые его значения приводятся ниже:

При t=1 вероятность Р отклонения выборочных величин от генеральных на величину однократной средней ошибки среднеарифметическая равна 0,683. Это означает, что в среднем каждая из тысячи единиц генеральной совокупности имеет вероятность обладать данным значением признака, но лишь 683 дадут гарантированные обобщенные показатели, которые будут отличатся от генеральных обобщенных показателей не более, чем на величину однократной средней ошибки среднеарифметической. Соответственно при t=2 вероятность Р=0,954, означает, что из каждой тысячи единиц генеральной совокупности 954 дадут обобщенные показатели, отличные от генеральных, не более, чем двукратную ошибку среднеарифметической.

При t=3 вероятность Р=0,997 означает, что 997 единиц из каждой тысячи единиц генеральной совокупности дадут обобщенные показатели, отличные от генеральных не более, чем на трехкратную ошибку среднеарифметической.

Пример:

ООО “Южный север” получило партию пряжи от недобросовестного поставщика, поэтому для изучения ее качества перед оплатой была проведена 4% механическая выборка, в результате которой было обследовано 100 одинаковых по весу образцов пряжи и получены следующие результаты (таблица 3)

Таблица 3

Требуется определить с вероятностью Р=0,683, Р=0,954 и Р=0,997, в каких пределах находится средняя крепость нити во всей партии пряжи. Примечание:

Среднюю выборочную арифметическую и выборочную дисперсию рассчитывать методом моментов или от условного нуля или от условной средней.

Нахождение выборочных характеристик в партии пряжи, закупленной ООО “Южный север”(таблица 4)

Таблица 4

Определим среднюю ошибку среднеарифметической, которая для данного вида отбора может быть найдена по формуле:

t - коэффициент доверия

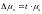
Пример: на основании данных представленного примера определить пределы, в которых будет находиться доля образцов пряжи в генеральной совокупности, обладающих крепостью нити меньшей 200 грамм. Расчеты предыдущей ошибки доли производится в следующей последовательности:

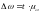
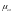- средняя ошибка доли, рассчитывается, как

m – число единиц, обладающих данным признаком