
- •Введение
- •1. Основы математического программирования
- •1.1. Постановка задачи математического программирования
- •1.2. Разновидности змп
- •1.3. Базовые понятия и терминология математического программирования
- •1.4. Производная по направлению. Градиент
- •1.5. Касательные гиперплоскости и нормали
- •1.6. Разложение Тейлора
- •1.7. Задача нелинейного программирования и условия существования ее решения
- •1.8. Задачи
- •2. Решение задачи нелинейного программирования без ограничений
- •2.1. Необходимые условия существования безусловного экстремума функции
- •2.2. Достаточные условия существования безусловного экстремума функции
- •2.3. Классический метод поиска безусловного экстремума
- •2.4. Задачи
- •3. Решение задачи нелинейного программирования при ограничениях-равенствах
- •3.1. Метод множителей Лагранжа
- •3.1.1. Назначение и обоснование метода
- •3.1.2. Схема реализации метода множителей Лагранжа
- •3.1.3. Интерпретация множителей Лагранжа
- •3.2. Метод подстановки
- •3.3. Задачи
- •4. Решение задачи нелинейного программирования при ограничениях-неравенствах
- •4.1. Обобщенный метод множителей Лагранжа
- •4.2. Условия Куна-Таккера
- •4.2.1. Необходимость условий Куна-Таккера
- •4.2.2. Достаточность условий Куна-Таккера в задачах выпукло-вогнутого программирования
- •4.2.3. Метод Куна-Таккера решения задачи выпукло-вогнутого программирования
- •4.3. Задачи
- •5. Численные методы решения знлп
- •5.1. Понятие алгоритма
- •5.3.2. Метод сопряженных градиентов
- •Описание алгоритма
- •5.3.3. Метод Ньютона
- •5.3.4. Метод Ньютона-Рафсона
- •Литература
- •Оглавление
3.1.3. Интерпретация множителей Лагранжа
Анализируя
значения множителей Лагранжа, можно
получить дополнительную ценную
информацию. С этим связано широкое
распространение метода множителей
Лагранжа. Множители Лагранжа измеряют
чувствительность оптимального значения
![]() к изменениям констант ограничений
к изменениям констант ограничений
![]() .
Это следует из утверждений следующей
теоремы.
.
Это следует из утверждений следующей
теоремы.
Теорема
Лагранжа. Пусть
![]() решение
задачи (3.4)-(3.5), а вектора
решение
задачи (3.4)-(3.5), а вектора
![]() определяющие строки матрицы Якоби
определяющие строки матрицы Якоби
![]() являются линейно независимыми. Тогда
существует единственный вектор множителей
Лагранжа
,
удовлетворяющий вместе с
являются линейно независимыми. Тогда
существует единственный вектор множителей
Лагранжа
,
удовлетворяющий вместе с
![]() системе условий (3.9), причем
системе условий (3.9), причем
![]() . (3.10)
. (3.10)
Во многих экономических задачах целевая функция имеет размерность стоимости (цены, умноженной на объем продукции) (прибыль, выручка, издержки), а с помощью ограничений вида (3.5) устанавливаются определенные значения затрат ресурсов. По-сути, в таких задачах множители Лагранжа измеряют чувствительность оптимального значения величины , имеющей размерность стоимости, к изменениям некоторого количества затрачиваемых ресурсов. В результате эти множители имеют размерность цены и по этой причине множители Лагранжа часто называют теневыми ценами (данного вида ресурсов).
Пример 3.1. Производственные издержки S компании определяются формулой
![]() ,
,
где
![]()
![]()
![]() – количества (у.е.) расходуемых ресурсов
вида 1, 2 и 3 соответственно. Технология
производства такова, что требует
выполнения следующих условий:
– количества (у.е.) расходуемых ресурсов
вида 1, 2 и 3 соответственно. Технология
производства такова, что требует
выполнения следующих условий:
![]()
Требуется решить задачу минимизации издержек S и определить значения обеспечивающие минимальные издержки.
Решение. Исходная задача сводится к следующей ЗНЛП:
![]()
Целевая функция и функции ограничений являются дифференцируемыми, поэтому в данном случае применим метод множителей Лагранжа.
Шаг
1. Вводим вектор множителей Лагранжа
![]() .
.
Шаг 2. Определяем функцию Лагранжа
![]()
![]() .
.
Шаг 3. Ищем стационарную точку, решая систему уравнений

Система имеет единственное решение. Соответствующая стационарная точка, подозрительная на экстремум, есть
![]() .
.
Шаг 4. Определяем тип экстремума в стационарной точке. Для этого нужно исследовать окаймленную матрицу Гессе
 .
.
Матрица
Якоби
![]() в произвольной точке
имеет вид
в произвольной точке
имеет вид
 .
.
Матрица Гессе функции Лагранжа в произвольной точке:

Таким образом, окаймленная матрица Гессе в произвольной, в том числе и в найденной стационарной точке имеет вид:

В
нашем случае
![]()
![]() .
Следовательно, надо проверить
.
Следовательно, надо проверить
![]() главный минор окаймленной матрицы
Гессе, начиная с минора порядка
главный минор окаймленной матрицы
Гессе, начиная с минора порядка
![]() то есть определитель полученной
окаймленной матрицы Гессе.
то есть определитель полученной
окаймленной матрицы Гессе.
Имеем:

Таким
образом, знак минора
![]() определяются знаком
определяются знаком
![]() .
Следовательно, целевая функция
имеет в стационарной точке
.
Следовательно, целевая функция
имеет в стационарной точке
![]() минимум, причем
минимум, причем
![]() .
.
Теперь можно сформулировать ответ: компания минимизирует свои издержки при условии использовании ресурсов видов 1, 2 и 3 в количестве 62,5; 25 и 12,5 у.е. соответственно.
Пример
3.2. Функция полезности набора из трех
товаров в количестве
и
![]() единиц соответственно, определяется
как
единиц соответственно, определяется
как
![]() .
.
Требуется
найти стоимость наиболее дешевого
набора товаров с заданным значением
полезности
![]() если цены товаров равны соответственно
4, 25 и 20 у.е.
если цены товаров равны соответственно
4, 25 и 20 у.е.
Решение. Требуется решить ЗНЛП
![]()
![]() .
.
Реализуем метод множителей Лагранжа.
Шаг
1. Поскольку имеется всего одно
ограничение, то вектор множителей
Лагранжа вырождается в скаляр
![]() .
.
Шаг 2. Определяем функцию Лагранжа
![]()
Шаг 3. Ищем стационарную точку, решая систему уравнений
 (3.11)
(3.11)
Умножая
1-е уравнение (3.11) на
![]() ,
2-е – на
,
2-е – на
![]() ,
3-е – на
,
получаем, с учетом 4-го уравнения той
же системы, эквивалентную систему
уравнений
,
3-е – на
,
получаем, с учетом 4-го уравнения той
же системы, эквивалентную систему
уравнений
 (3.12)
(3.12)
Из
1-го и 3-го уравнений (3.12) имеем
![]() ;
из 2-го и 3-го –
;
из 2-го и 3-го –![]() .
Подстановка этих выражений в 4-е уравнение
(3.12) дает
.
Подстановка этих выражений в 4-е уравнение
(3.12) дает
![]() ,
откуда
,
откуда
![]() и далее простыми подстановками в
последние соотношения находим искомые
значения компонент единственной
стационарной точки:
и далее простыми подстановками в
последние соотношения находим искомые
значения компонент единственной
стационарной точки:
![]()
Шаг
4. Для определения типа экстремума
функции
![]() в точке
нужно исследовать окаймленную матрицу
Гессе
в точке
нужно исследовать окаймленную матрицу
Гессе
.
Поскольку матрица Якоби в произвольной точке есть вектор-строка
![]() ,
,
то подстановка значений компонент стационарной точки дает
![]() .
.
Матрица Гессе функции Лагранжа в произвольной точке:

откуда после подстановки значений компонент стационарной точки
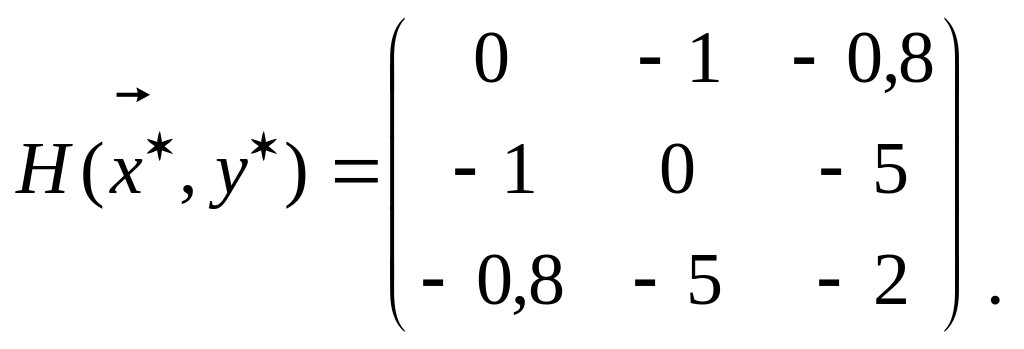
Таким образом, окаймленная матрица Гессе в найденной стационарной точке принимает вид:

В
нашем случае
![]() .
Следовательно, надо проверить
.
Следовательно, надо проверить
![]() главных минора окаймленной матрицы
Гессе, начиная с минора порядка
главных минора окаймленной матрицы
Гессе, начиная с минора порядка
![]()
Имеем:


Таким
образом, знаки миноров определяются
знаком
![]() .
Следовательно, найденная стационарная
точка
определяет набор товаров, обладающий
полезностью 1000 и минимальной стоимостью
в размере
.
Следовательно, найденная стационарная
точка
определяет набор товаров, обладающий
полезностью 1000 и минимальной стоимостью
в размере
![]() у.е.
Чувствительность достигнутого значения
у.е.
Чувствительность достигнутого значения
![]() к изменению полезности набора товаров
при этом равна
к изменению полезности набора товаров
при этом равна
![]() .
.
