4.2.1. Необходимость условий Куна-Таккера

Преобразуем ограничения-неравенства в (4.2) к виду ограничений-равенств. Для этого к левым частям каждого -го неравенства прибавим неотрицательные дополнительные переменные , подобранные таким образом, что все ограничения исходной задачи предстают в виде ограничений-равенств.

Обозначим Тогда исходная ЗНЛП (4.1)-(4.2) принимает вид

В развернутой форме она записывается следующим образом:

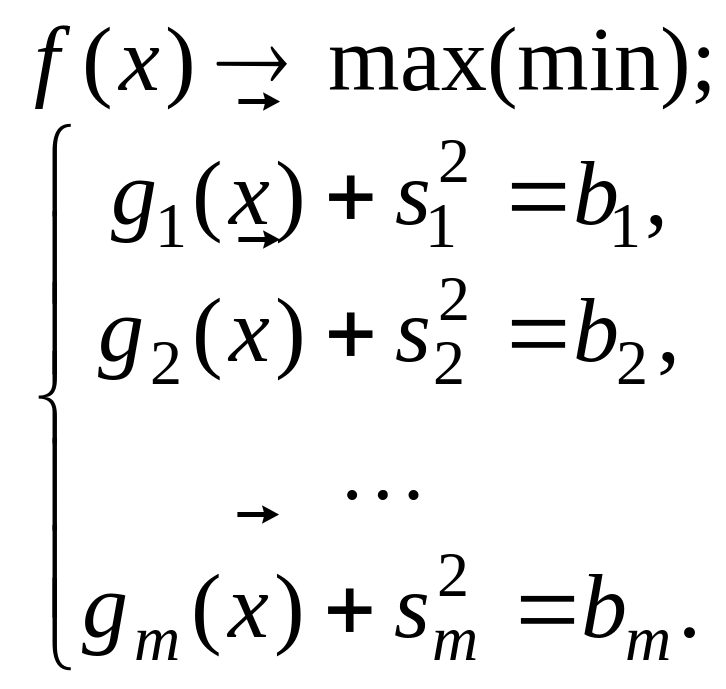(4.5)

Полученную ЗНЛП с ограничениями-равенствами можно решить методом Лагранжа. Функция Лагранжа задачи (4.5) есть

,

или, в подробной записи,

. (4.6)

Необходимым условием существования экстремума целевой функции при ограничениях-равенствах является наличие стационарной точки функции Лагранжа. В стационарной точке все производные функции Лагранжа равны нулю, поэтому из (4.6) следует, что стационарной точкой является любое решение системы уравнений

(4.7)

Из уравнений второй строки системы (4.7) следует . Отсюда, с учетом уравнений третьей строки системы (4.7) получаем

. (4.8)

Условие (4.8) называется условием дополняющей нежесткости.

Покажем, что необходимым условием существования экстремума целевой функции в задаче (4.1)-(4.2) является условие , в задаче максимизации (когда ) и условие в задаче минимизации (когда ).

Действительно, по теореме Лагранжа

,

то есть множители Лагранжа выражают скорость изменения целевой функции по отношению к изменениям правой части ограничений. Поскольку увеличение правых частей неравенств способствует лишь увеличению множества допустимых значений аргумента , то это означает, что значение максимума целевой функции не уменьшится при таком увеличении, то есть . Совершенно аналогично показывается, что условием существования экстремума целевой функции в задаче минимизации является условие .

Таким образом, объединяя (4.7) и (4.8) с условиями неотрицательности (неположительности) множителей Лагранжа, получаем систему условий существования экстремума функции при ограничениях-неравенствах, которые можно сформулировать в виде следующей теоремы.

Теорема Куна-Таккера. Пусть и определяют стационарную точку функции Лагранжа задачи (4.1)-(4.2).

Тогда справедливы следующие условия (Куна-Таккера):

(4.9)

Замечание 4.2. Из 1-го и 3-го условий Куна-Таккера следует, что либо множитель Лагранжа равен нулю, либо соответствующее ограничение выполняется как точное равенство, либо и то и другое выполняются одновременно.

4.2.2. Достаточность условий Куна-Таккера в задачах выпукло-вогнутого программирования

Условия Куна-Таккера для задачи (4.1)-(4.2) оказываются достаточными, если целевая функция и область ограничений обладают определенными свойствами, связанными с выпуклостью и вогнутостью, и указанными в таб. 4.1.

Таблица 4.1

Тип экстремума	Целевая функция	Область ограничений
максимум	вогнутая	выпуклое
минимум	выпуклая	выпуклое

Нетрудно показать, что множество является выпуклым множеством при условии, что функция выпукла на . Поскольку пересечение выпуклых множеств является выпуклым множеством, то достаточным условием выпуклости области ограничений в задаче (4.1)-(4.2) является условие выпуклости всех функций ограничений. В частности, в случае линейных ограничений допустимое множество всегда будет выпуклым (а именно – выпуклым многогранником).

Свойства выпуклости и вогнутости являются настолько значимыми, что порождают два широко распространенных класса задач нелинейного программирования.

Задачей выпуклого программирования называется ЗНЛП

(4.10)

если целевая функция является выпуклой функцией, а область ограничений есть выпуклое множество.

Задачей вогнутого программирования называется ЗНЛП

(4.11)

если целевая функция является вогнутой функцией, а область ограничений есть выпуклое множество.

Следующая теорема позволяет обосновать изложенный ниже метод решения задачи выпукло-вогнутого программирования (метод Куна-Таккера).

Теорема о единственности экстремума строго выпуклой (вогнутой) функции. Строго выпуклая (строго вогнутая) функция на выпуклом множестве не может иметь более одной точки глобального минимума (максимума).