
- •Введение
- •1. Основы математического программирования
- •1.1. Постановка задачи математического программирования
- •1.2. Разновидности змп
- •1.3. Базовые понятия и терминология математического программирования
- •1.4. Производная по направлению. Градиент
- •1.5. Касательные гиперплоскости и нормали
- •1.6. Разложение Тейлора
- •1.7. Задача нелинейного программирования и условия существования ее решения
- •1.8. Задачи
- •2. Решение задачи нелинейного программирования без ограничений
- •2.1. Необходимые условия существования безусловного экстремума функции
- •2.2. Достаточные условия существования безусловного экстремума функции
- •2.3. Классический метод поиска безусловного экстремума
- •2.4. Задачи
- •3. Решение задачи нелинейного программирования при ограничениях-равенствах
- •3.1. Метод множителей Лагранжа
- •3.1.1. Назначение и обоснование метода
- •3.1.2. Схема реализации метода множителей Лагранжа
- •3.1.3. Интерпретация множителей Лагранжа
- •3.2. Метод подстановки
- •3.3. Задачи
- •4. Решение задачи нелинейного программирования при ограничениях-неравенствах
- •4.1. Обобщенный метод множителей Лагранжа
- •4.2. Условия Куна-Таккера
- •4.2.1. Необходимость условий Куна-Таккера
- •4.2.2. Достаточность условий Куна-Таккера в задачах выпукло-вогнутого программирования
- •4.2.3. Метод Куна-Таккера решения задачи выпукло-вогнутого программирования
- •4.3. Задачи
- •5. Численные методы решения знлп
- •5.1. Понятие алгоритма
- •5.3.2. Метод сопряженных градиентов
- •Описание алгоритма
- •5.3.3. Метод Ньютона
- •5.3.4. Метод Ньютона-Рафсона
- •Литература
- •Оглавление
1.4. Производная по направлению. Градиент
Пусть
![]() произвольный
вектор единичной длины, то есть
произвольный
вектор единичной длины, то есть
![]() .
Производной функции
в точке
.
Производной функции
в точке
![]() по направлению
по направлению
![]() называется предел
называется предел
![]() .
.
По
сути
![]() это
скорость изменения значения функции
в точке
при перемещении аргумента в направлении
вектора
.
это
скорость изменения значения функции
в точке
при перемещении аргумента в направлении
вектора
.
Градиентом
функции
в точке
называется
вектор
![]() ,
компоненты которого равны частным
производным первого порядка данной
функции в точке
,
компоненты которого равны частным
производным первого порядка данной
функции в точке
![]()
![]() .
.
Теорема о производной по направлению. Производная функции в точке по направлению может быть найдена по формуле
![]() . (1.14)
. (1.14)
Теорема о градиенте. Градиент функции указывает направление наискорейшего роста функции в точке . При этом максимальная скорость роста равна модулю градиента в этой точке:
![]() . (1.15)
. (1.15)
Доказательство.
Пусть
![]() угол
между векторами
и
.
Так как скалярное произведение
угол
между векторами
и
.
Так как скалярное произведение
![]() этих
векторов может быть найдено по формуле
этих
векторов может быть найдено по формуле
![]() ,
,
а , то из формулы (1.14) вытекает
![]() .
.
Последнее
означает, что производная по направлению
принимает наибольшее значение при
![]() ,
то есть когда векторы
,
то есть когда векторы
![]() и
имеют одинаковое направление. Теорема
доказана.
и
имеют одинаковое направление. Теорема
доказана.
Пример
1.2. Найти производную функции
![]() в точке
в точке
![]() по направлению вектора
по направлению вектора
![]()
Решение.
Вектор
![]() задает единичный вектор
задает единичный вектор
![]() того же направления. Имеем
того же направления. Имеем
![]()
Градиент
![]() в произвольной точке
равен
в произвольной точке
равен
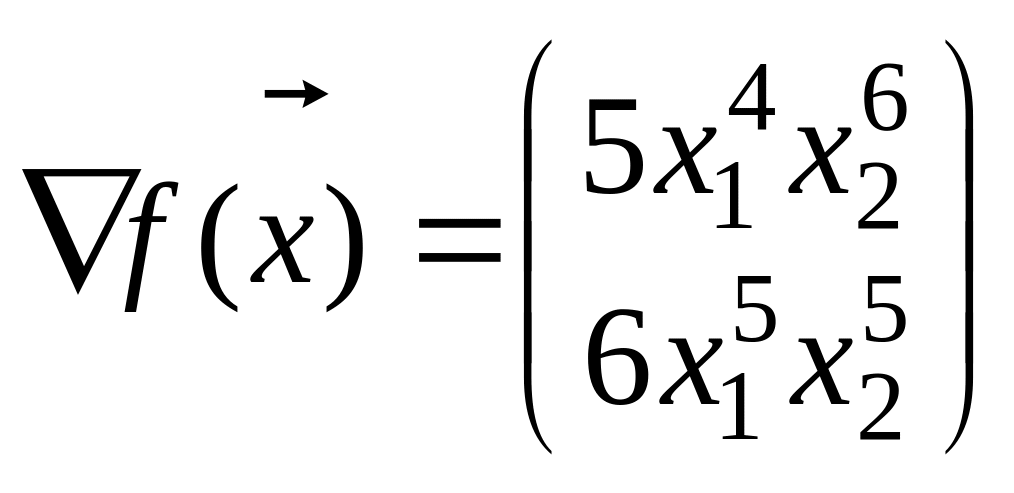 ,
поэтому
,
поэтому
![]() .
Подставляя найденные значения компонент
и
в (1.14), получаем
.
Подставляя найденные значения компонент
и
в (1.14), получаем
![]() .
.
1.5. Касательные гиперплоскости и нормали
Пусть
![]() некоторое
фиксированное число. Множеством уровня
некоторое
фиксированное число. Множеством уровня
![]() функции
называется множество всех точек,
удовлетворяющих уравнению
функции
называется множество всех точек,
удовлетворяющих уравнению
![]() .
.
Пример
1.3. Для функции двух переменных
![]() при
при
![]() множеством уровня
множеством уровня
![]() является эллипс
является эллипс
![]() (рис. 1.1)
(рис. 1.1)

Рис.
1.1. Нормаль
![]() к эллипсу в точке
к эллипсу в точке
![]()
В
плоском (двумерном) случае, когда
![]() ,
множество уровня
функции
является линией. В трехмерном –
поверхностью.
,
множество уровня
функции
является линией. В трехмерном –
поверхностью.
Касательной
гиперплоскостью к множеству уровня
функции
в точке
из этого множества называется множество
всех точек
![]() ,
удовлетворяющих уравнению
,
удовлетворяющих уравнению
![]() . (1.16)
. (1.16)
В плоском случае касательная гиперплоскость является касательной прямой; в трехмерном случае – обычной касательной плоскостью.
Пример
1.4. Касательной гиперплоскостью для
функции
из предыдущего примера в точке
![]() является прямая
является прямая
![]() , (1.17)
, (1.17)
где
![]() ;
;
![]() ;
;
![]() (см. рис.1.1).
(см. рис.1.1).
Вектором нормали (нормалью) к гиперплоскости, задаваемой уравнением
![]() , (1.18)
, (1.18)
называется
вектор
,
компоненты которого равны компонентам
заданного в (1.18) вектора
![]() ,
то есть
,
то есть
![]() .
Вектор нормали ортогонален своей
гиперплоскости. В плоском и трехмерном
случаях ортогональность означает
перпендикулярность.
.
Вектор нормали ортогонален своей
гиперплоскости. В плоском и трехмерном
случаях ортогональность означает
перпендикулярность.
Из уравнения (1.16) следует, что градиент функции является нормалью гиперплоскости к множеству уровня
![]() .
.
Пример 1.5. Нормалью к касательной прямой (1.17) является (см. рис.1.1) вектор
![]()
1.6. Разложение Тейлора
Пусть
![]() вектор
с целочисленными неотрицательными
компонентами. Обозначим через
вектор
с целочисленными неотрицательными
компонентами. Обозначим через
![]() сумму его компонент. Говорят, что функция
сумму его компонент. Говорят, что функция
![]() есть «о малое» по сравнению с
есть «о малое» по сравнению с
![]() при
при
![]() (пишут
(пишут
![]() ,
если справедливо условие
,
если справедливо условие
![]() . (1.19)
. (1.19)
Условие
(1.19) означает, что
![]() пренебрежимо мала по сравнению с
при
.
Если функция
пренебрежимо мала по сравнению с
при
.
Если функция
![]() )
дифференцируема
)
дифференцируема
![]() раз в некоторой окрестности
раз в некоторой окрестности
![]() точки
точки
![]() ,
то для всякой точки
,
то для всякой точки
![]() справедлива
формула Тейлора
справедлива
формула Тейлора
 +
+
![]() . (1.20)
. (1.20)
Величина
![]() называется остаточным членом в форме
Пеано и означает пренебрежимо
малую величину по сравнению с
называется остаточным членом в форме
Пеано и означает пренебрежимо
малую величину по сравнению с
![]() при
при
![]() .
.
Представление функции по формуле Тейлора (1.20) называется разложением Тейлора этой функции в точке с точностью до производных m-го порядка.
В частности, разложение Тейлора с точностью до производных второго порядка есть
![]() (1.21)
(1.21)
где![]() матрица
Гессе функции
в точке
.
матрица
Гессе функции
в точке
.
В
одномерном случае, когда
![]() и
функция
является функцией одной переменной,
формула Тейлора принимает вид
и
функция
является функцией одной переменной,
формула Тейлора принимает вид
![]() (1.22)
(1.22)
Если функция является аналитической функцией, то есть дифференцируемой в точке бесконечное число раз, то она может быть разложена в степенной ряд (ряд Тейлора):
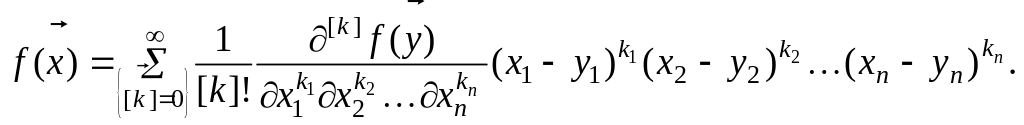 (1.23)
(1.23)
В одномерном случае, когда , из (1.22) и (1.23) следует
![]() (1.24)
(1.24)
Пример 1.6. Из (1.24) следует, в частности,
![]() ;
;
![]()
