
Методы оптимизации и исследование операций для бакалавров информатики. Часть 2
.pdf

УДК 517.8 Г 522
Гладких Б. А. Методы оптимизации и исследование
Г522 операций для бакалавров информатики. Ч. II. Нелинейное и динамическое программирование: учебное пособие.
— Томск: Изд-во НТЛ, 2011. — 264 с.
ISBN 978-5-89503-483-5
Книга написана на основе лекций, в течение ряда лет читавшихся автором на факультете информатики Томского государственного университета.
Во вторую часть вошли разделы, относящиеся к нелинейному программированию (общая теория выпуклого программирования, одномерная оптимизация, многомерная оптимизация без ограничений, оптимизация с ограничениями), а также элементарное введение в динамическое программирование. Обсуждаются вопросы практической оптимизации с помощью популярных пакетов прикладных программ.
Учебное пособие соответствует Государственному образовательному стандарту по направлениям «информационные технологии» и «прикладная информатика», но может быть использовано для студентов, обучающихся по другим инженерным и экономическим
направлениям.
УДК 517.8
Р е ц е н з е н т ы:
доктор техн. наук, профессор В. В. Поддубный, кандидат техн. наук, доцент А. П. Рыжаков
ISBN 978-5-89503-483-5 |
c |
Б. А. Гладких, 2011 |
|
|
c |
|
Издательство НТЛ, |
|
обложка, 2011 |
Оглавление
Введение |
|
5 |
9. Теория выпуклого программирования |
|
13 |
9.1. Евклидово пространство . . . . . . . . . . . . . . . . . . . . |
14 |
|
9.2. Выпуклые функции и их свойства . . . . |
. . . . . . . . . . |
25 |
9.3. Классические задачи оптимизации . . . . |
. . . . . . . . . . |
39 |
9.4. Теорема Куна — Таккера . . . . . . . . . . |
. . . . . . . . . . |
46 |
9.5. Дифференциальные условия Куна — Таккера и их гео- |
|
|
метрическая интерпретация . . . . . . . . |
. . . . . . . . . . |
51 |
9.6. Частные случаи . . . . . . . . . . . . . . . |
. . . . . . . . . . |
59 |
9.7. Квадратичное программирование. Метод Вулфа . . . . . . |
65 |
|
9.8. Исторические замечания . . . . . . . . . . |
. . . . . . . . . . |
70 |
10. Одномерная оптимизация |
|
75 |
10.1. Классификация одномерных методов . . . |
. . . . . . . . . . |
76 |
10.2. Грубая локализация минимума . . . . . . |
. . . . . . . . . . |
78 |
10.3. Минимизация унимодальных функций . . |
. . . . . . . . . . |
80 |
10.4. Метод парабол . . . . . . . . . . . . . . . . |
. . . . . . . . . . |
83 |
10.5. Метод касательных . . . . . . . . . . . . . |
. . . . . . . . . . |
85 |
10.6. Метод Ньютона . . . . . . . . . . . . . . . |
. . . . . . . . . . |
87 |
10.7. Исторические замечания . . . . . . . . . . |
. . . . . . . . . . |
89 |
11. Многомерная оптимизация без ограничений |
91 |
|
11.1. Релаксационные методы оптимизации . . . . . . . . . . . . |
91 |
|
11.2. Методы нулевого порядка . . . . . . . . . |
. . . . . . . . . . |
98 |
11.3. Градиентные методы . . . . . . . . . . . . |
. . . . . . . . . . |
108 |
11.4. Ньютоновские и квазиньютоновские методы . . . . . . . . |
114 |
|
11.5. Оптимизация невыпуклых функций . . . |
. . . . . . . . . . |
129 |

4 |
Оглавление |
|
11.6. Исторические замечания . . . . . . . . . . |
. . . . . . |
. . . . 146 |
12. Многомерная оптимизация с ограничениями |
154 |
|
12.1. Сведение к задаче без ограничений . . . . . |
. . . . . |
. . . . 156 |
12.2. Общая схема релаксационных методов, |
учитывающих |
|
ограничения . . . . . . . . . . . . . . . . . . |
. . . . . |
. . . . 163 |
12.3. Метод проектирования градиента . . . . . . |
. . . . . |
. . . . 169 |
12.4. Последовательное квадратичное программирование |
. . . . 183 |
|
12.5. Метод линейной аппроксимации . . . . . . . |
. . . . . |
. . . . 193 |
12.6. Метод секущих плоскостей . . . . . . . . . . |
. . . . . |
. . . . 199 |
12.7. Исторические замечания . . . . . . . . . . . |
. . . . . |
. . . . 208 |
13. Практическая оптимизация с помощью пакетов |
|
|
прикладных программ |
|
210 |
13.1. Оптимизация в пакете Excel . . . . . . . . . |
. . . . . |
. . . . 211 |
13.2. Оптимизация в пакете MATLAB . . . . . . |
. . . . . |
. . . . 218 |
13.3. Оптимизация в интернете . . . . . . . . . . |
. . . . . |
. . . . 228 |
14. Динамическое программирование |
|
235 |
14.1. Задача о кратчайшем пути . . . . . . . . . . |
. . . . . |
. . . . 236 |
14.2. Задача об инвестициях . . . . . . . . . . . . |
. . . . . |
. . . . 245 |
14.3. Непрерывная оптимизация . . . . . . . . . . |
. . . . . |
. . . . 250 |
14.4. Исторические замечания . . . . . . . . . . . |
. . . . . |
. . . . 256 |
Литература |
|
261 |
Введение
Общая задача математического программирования имеет вид
|
|
X ) |
→ |
min (max); |
(1) |
||
|
f (→− |
|
|
||||
|
i(→− |
|
|
|
(2) |
||
|
X ) |
|
|
|
0, i = 1, . . . , m, |
|
|
g |
= |
|
|||||
|
|
|
|
|
|
|
|
где (1) — целевая функция (objective function), (2) — ограничения
(constrains).
→−
Размерность вектора переменных X = (x1, . . . , xn)T предполагается конечной, поэтому задачу математического программирования называют конечномерной оптимизацией в отличие от бесконечномерных задач вариационного исчисления (variational calculus).
В случае, когда когда f и gi являются линейными функциями, математическое программирование превращается в линейное (linear programming — LP), которому мы посвятили всю первую часть нашего курса, a когда хотя бы одна из функций f и gi нелинейна, мы имеем дело с задачей нелинейного программирования (nonlinear programming — NLP).
Задачи нелинейного программирования возникают в различных областях деятельности, когда линейное приближение реальных зависимостей является слишком грубым. Огромное число задач такого рода возникает при автоматизации проектирования и оптимизации технологических процессов. Например, в
6 |
Введение |
[23, кн. 2, с. 273] описывается нелинейная модель оптимизации химического процесса синтеза этиленгликоля, имеющая 22 переменные, 7 ограничений-равенств, 12 ограничений-неравенств и полный набор ограничений переменных сверху и снизу.
В отличие от линейного программирования, где целевая функция представляла собой простейшую линейную форму и проблем с ее определением не было, здесь возможны различные варианты.
Вреальных задачах целевая функция может быть задана:
•аналитическим выражением, которое может быть сколь угодно сложным;
•алгоритмом вычисления, в том числе программой имитационного моделирования некоторого процесса;
•натурным экспериментом.
Таким образом, само вычисление значения целевой функции при заданных значениях независимых переменных, не говоря уже о ее оптимизации, может представлять определенную проблему и требовать немалых затрат труда.
Множество D Rn, определяемое совокупностью ограничений (2), называется множеством допустимых решений (feasible decisions set) или (в русскоязычной литературе) множеством планов.
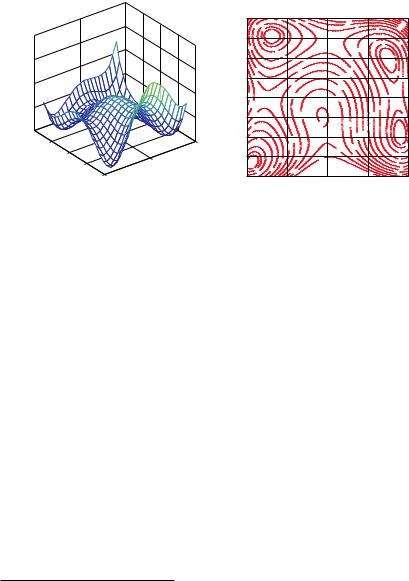
Когда число переменных равно двум, задачу математического программирования легко интерпретировать геометрически. Множество допустимых решений будет представлять собой некоторую область на плоскости, а целевая функция f (x1, x2) имеет вид неровной поверхности с холмами и впадинами. Ее можно изобразить
ввиде трехмерной картинки или, подобно тому, как на географических картах изображается рельеф местности, семейством линий равных значений — изоцелевых линий (рис. 1). Как мы увидим
вдальнейшем, найти точку глобального экстремума (минимума или максимума) для таких функций бывает очень сложно, алгоритм поиска может заблудиться в сильно изрезанном рельефе.
Введение |
7 |
400 
300 
200 
100 
0 
4
2 |
5 |
0
0
−2
−4 −5
4 |
|
40 |
20 |
|
|
||||
|
|
|||
|
|
|
|
10 |
3 |
|
|
10 |
|
|
60 |
|
|
|
2 |
|
|
|
|
|
|
80 |
|
|
1 |
100 |
|
||
0 |
140 |
120 |
|
|
|
|
|
|
|
−1 |
|
100 |
|
|
|
80 |
|
|
|
−2 |
60 |
40 |
||
|
|
|||
−3 |
|
|
|
|
|
|
5 |
|
|
−4 |
|
20 |
||
|
|
|
|
|
−4 |
|
|
|
|
|
40 |
|
60 |
80 |
5 |
|
|
||
|
|
|
|
|
20 |
|
|
|
|
|
40 |
60 |
80 |
|
|
|
|
||
|
|
|
100 |
|
|
|
|
120 |
|
|
|
|
140 |
|
|
|
|
160 |
|
|
|
120 |
|
|
|
|
100 |
|
|
|
80 |
|
140 |
|
60 |
|
|
160 |
|
|
|
|
|
|
|
−2 |
|
|
|
100 |
|
60 |
120 |
|
80 |
|
100 |
|
|
|
|
|
|
|
|
|
|
8 |
||
|
|
|
|
20 |
10 |
40 |
0 |
||
|
|
|
|
|
|
||||
|
|
40 |
|
|
|
|
|
|
|
|
|
60 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
80 |
|
|
10 |
|
|
|
|
|
100 |
|
|
20 |
|
||||
|
120 |
|
|
|
|
|
|
||
|
140 |
|
|
|
|
|
|
|
|
|
160 |
|
|
|
20 |
|
|
|
|
|
|
|
|
60 |
40 |
|
|
|
|
|
|
|
|
|
10 |
|
|||
180 |
|
|
|
80 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
100 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
120 |
|
|
|
5 |
|
0 |
|
|
180 |
140 |
|
|
|
1 |
|||
|
|
|
|
|
20 |
|
|||
|
160 |
|
|
|
|
||||
200 |
|
|
|
40 |
|
|
|||
|
|
|
|
|
|
60 |
|
|
|
|
|
|
|
|
|
80 |
|
||
|
|
|
|
200 |
|
120 |
|
|
|
|
|
|
|
|
160 |
||||
0 |
|
|
|
2 |
|
|
|
|
4 |
Рис. 1. Пример сложной целевой функции. Трехмерный рельеф и изоцелевые линии
Трудности, В линейном программировании, когда f и gi порождаемые были линейными функциями, мы доказали нелинейностью ряд фундаментальных свойств, существенно
облегчающих задачу:
•множество планов представляет собой выпуклую многогранную область с конечным числом крайних точек;
• |
оптимальный план |
→− |
|
находится в крайней точке множе- |
|
|
X |
|
|
|
ства планов; |
|
|
|
•локальный экстремум всегда является глобальным.
Внелинейном программировании все значительно сложнее.
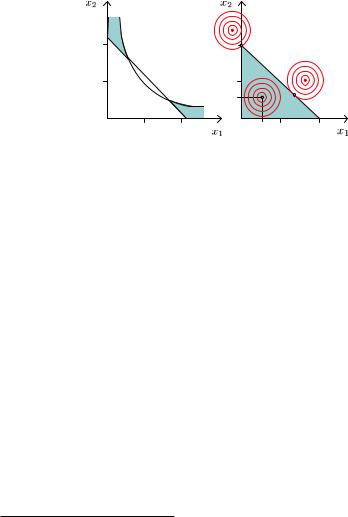
Во-первых, множество планов может быть не только невыпуклым, но даже несвязным. Пример такого множества представлен на рис. 2, a. Оно задается следующими неравенствами1:
g1(x1, x2) = x1x2 1,
1В данной книге в численных примерах для отделения целой части числа от дробной мы будем, следуя зарубежной традиции, пользоваться не запятой, а
8 |
Введение |
|
g2(x1, x2) = x1 + x2 2.2, |
|
||||
|
x1, x2 0. |
|
|
|
|
|
2 |
|
|
2 |
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
b |
|
|
|
0 |
1 |
2 |
0 |
a |
1 |
2 |
|
|
а) |
|
|
б) |
|
Рис. 2. Трудности, порождаемые нелинейностью
Во-вторых, экстремум может находиться как на границе, так и внутри области. В примере на рис. 2, б целевая функция представляет собой простейшую квадратичную форму двух перемен-
ных, изоцелевые линии которой являются концентрическими ок-
→−
ружностями с общим центром в точке X = (a, b)T :
f1(x1, x2) = (x1 − a)2 + (x2 − b)2 → min, g(x1, x2) = x1 + x2 1,
x1, x2 0.
В зависимости от значений a и b оптимальный план находится в крайней точке, на границе или внутри треугольной области
планов.
В-третьих, целевая функция может иметь несколько локальных экстремумов, что демонстрирует пример на рис. 1, однако основная задача нелинейного программирования состоит в нахождении самого лучшего из них — глобального — оптимума.
десятичной точкой. Запятые будут использоваться для отделения чисел друг от друга. Так значительно удобнее записывать векторы с нецелыми компонентами.
Введение |
9 |
Классификация
В связи с указанными трудностями общих ме-
тодов решения любых задач математического задач и методов. программирования не существует. Изобрете-
Структура книги
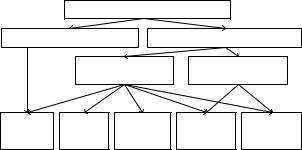
ны сотни различных методов, но ни один из них по силе и универсальности не может сравниться с симплексным алгоритмом линейного программирования. Давно замечено, что если от некоторой болезни имеется много лекарств, то это верный признак того, что данный недуг радикально неизлечим. Поэтому единственный возможный путь в этой ситуации — выделять специфические классы нелинейных задач и для каждого из них искать свои подходы (рис. 3).
Математическое программирование
Линейное программирование |
Нелинейное программирование |
Выпуклое |
Невыпуклое |
программирование |
программирование |
Линей - |
Квадра- |
Одномер - |
Задачи без |
Задачи с |
ные |
тичные |
ные |
ограни - |
ограниче - |
задачи |
задачи |
задачи |
чений |
ниями |
Рис. 3. Классификация задач математического программирования
К настоящему времени наиболее изученным является класс задач выпуклого программирования (convex programming), в которых целевая функция и ограничения задаются выпуклыми функциями. Важнейшим свойством таких задач является единственность экстремума, то есть совпадение локального экстремума с глобальным. Для выпуклых задач удается построить общую теорию, которую мы будем изучать в гл. 9. Она обобщает классический метод множителей Лагранжа и сводит задачу нахождения экстремума при наличии ограничений к решению некоторой системы уравнений и неравенств (условий Куна — Таккера).
Как известно, линейные функции также являются выпуклыми, поэтому с теоретической точки зрения линейное программи-
