
Методы оптимизации и исследование операций для бакалавров информатики. Часть 2
.pdf40 |
|
|
|
|
|
Глава 9. |
Теория выпуклого программирования |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X ) |
можно аппроксими- |
||||||||||
как в окрестности этой точки функцию f (→− |
|||||||||||||||||||||||||||
ровать квадратичной функцией |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Q(→− ) = |
f |
(→− |
|
)+ |
→− |
→− |
→− →− |
|
)+ |
|
→− →− |
|
|
→− |
→− →− |
|
). |
||||||||||
X |
X |
|
|
T f (X |
)(X |
− |
X |
|
1 (X |
− |
X |
|
)T H(X |
)(X |
− |
X |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
X |
) |
положительно определена, то |
Q(X ) |
является выпук- |
||||||||||||||||||||||
Если H(→− |
|
|
|
→− |
|||||||||||||||||||||||
лой, и точка |
|
→− |
доставляет ей минимум. Таким образом, для вы- |
||||||||||||||||||||||||
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
пуклых функций условие первого порядка является необходимым и достаточным.
Следующий случай чуть сложнее. Он поОграничения на хож на предыдущий, но в базовом курнеотрицательность се матанализа рассматривается реже, поэтому его можно отнести к «полуклассическим». Единственным видом ограничений является неотрица-
тельность переменных, задача имеет вид
−→
f (X ) = f (x1, . . . , xn) → min, 0 xj < ∞, j = 1, . . . , n.
Легко показать, что необходимое условие минимума (9.15) для каждой переменной в этом случае имеет вид
|
|
∂f |
(→− |
|
|
|
|
||
а) |
|
X ) |
|
0, |
|
|
|||
|
∂xj |
|
|
||||||
|
|
|
|
X ) |
|
|
|
||
б) |
xj |
∂f (→− |
= 0, |
(9.17) |
|||||
|
|||||||||
|
|
|
|
∂xj |
|
|
|
|
|
в) |
xj 0, |
|
|
|
|
||||
|
j = 1, . . . , n. |
|
|
||||||
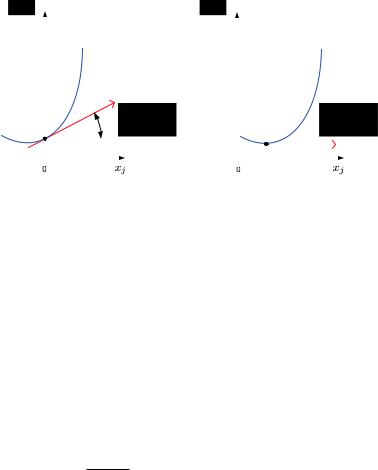
Чтобы убедиться в этом, рассмотрим рис. 9.11. На нем изоб- |
|||||||||
ражены два варианта сечения функции |
X ) |
по одной из коор- |
|||||||
f (→− |
|||||||||
динат xj . В левом варианте безусловный минимум функции по этой переменной находится в области отрицательных значений.
9.3.. Классические задачи оптимизации |
41 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 9.11. Условная оптимизация по одной переменной с ограничением на ее неотрицательность
Поскольку одномерная функция сечения выпукла и справа от минимума возрастает, то ограничение на неотрицательность является в данном случае активным. Минимум достигается в нуле, а производная в этой точке неотрицательна.
Справа иллюстрируется случай, когда точка безусловного минимума по xj находится на положительной полуоси и ограничение на неотрицательность неактивно. В этом случае необходимым условием минимума является обычное равенство нулю первой производной.
Условия (9.17) являются алгебраическим воплощением дан-
ных геометрических построений. Если xj > 0, то условие «б»
−→
∂f (X ) = 0, условие «а» ему не противоречит,
∂xj
если же xj = 0, то работает условие «a», а условие «б» при этом не работает.
В векторной форме условия (9.17) приобретают вид
−→ −→
a) f (X ) 0,
→− T →− →−
б) X f (X ) = 0,
→−
в) X 0.
42 |
Глава 9. |
Теория выпуклого программирования |
|
||||||||
Если оптимизируемая функция выпукла, эти условия являют- |
|||||||||||
ся не только необходимыми, но и достаточными. |
|||||||||||
Ограничения- |
Еще один классический случай имеет место, ко- |
||||||||||
равенства |
гда ограничения задаются совокупностью урав- |
||||||||||
нений, в этом случае условная экстремальная за- |
|||||||||||
|
|||||||||||
дача приобретает вид |
|
|
|
|
|
|
|
|
|||
|
|
X ) = f (x , . . . , x |
|
) |
|
min, |
|||||
|
|
f (→− |
1 |
|
n |
|
→ |
|
|
||
|
|
|
|
|
|
|
|
||||
|
X ) = g |
(x , . . . , x ) = 0, i = 1, . . . , m. |
|||||||||
gi(→− |
i |
1 |
|
n |
|
|
|
|
|
||
Стандартный подход к решению этой задачи [15, с. 35] основан на использовании функции Лагранжа (лагранжиана)
|
|
|
|
|
|
|
m |
|
|
|
|
L(X , Y ) = f (X ) + |
y g |
(X ), |
(9.18) |
||||
|
|
→− →− |
→− |
|
i i |
→− |
|||
|
|
|
|
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
i |
|
|
зависящей |
не только |
от |
оптимизируемых |
переменных |
|||||
X |
= (x |
, . . . , x )T |
, |
но |
и от |
дополнительных |
переменных |
||
→− |
1 |
n |
|
||||||
Y |
= (y , . . . , y )T |
— так |
называемых множителей Лагран- |
||||||
→− |
1 |
m |
|||||||
жа (Lagrange multipliers), число которых равно количеству ограничений.
Необходимые (и достаточные в случае выпуклости всех участ-
вующих функций) условия минимума имеют вид |
|
|||
|
∂L(→− →− |
|
|
|
|
X , Y ) |
= 0, j = 1, . . . , n; |
(9.19) |
|
|
∂xj |
|
||
|
|
|
||
|
∂L(→− →− |
|
|
|
|
X , Y ) |
|
= 0, i = 1, . . . , m. |
(9.20) |
|
∂yi |
|||
|
|
|
||
Несмотря на всю неочевидность этого утверждения, оно объясняется довольно просто. Для начала предположим, что имеется задача минимизации при единственном ограничении. На рис. 9.12, представляющем двумерный случай, жирной линией изображе-
но множество допустимых точек, удовлетворяющих уравнению
−→ −→ g(X ) = 0 на фоне семейства изолиний целевой функции f (X ).

9.3.. Классические задачи оптимизации |
43 |
|
|
|
|
|
|
|
Рис. 9.12. Условная оптимизация с одним ограничением-равенством
Задача состоит в том, чтобы найти такую допустимую точку, которой соответствует наименьшее значение целевой функции. Двигаясь по допустимой кривой, например сверху вниз, мы будем пересекать изоцелевые линии, уменьшая значение целевой
функции до тех пор, пока не достигнем точки касания с одной из
−→
них. Это и есть искомая точка оптимума X . В ней касательные
прямые к допустимой кривой и изоцелевой линии совпадают, следовательно, вектор нормали к изоцелевой линии, определяемый
|
|
|
|
X ) |
|
|
X ) |
||
градиентом целевой функции →− f (→− , должен быть коллинеарен |
|||||||||
|
|
|
|
|
|
|
|
|
|
вектору нормали к допустимой кривой →− g(→− , т. е. |
|||||||||
→− f (→− |
|
) = λ |
→− →− |
|
), |
||||
|
X |
|
|
g(X |
|
||||
|
|
|
|
|
|
|
|
||
где λ — произвольный множитель (множитель Лагранжа). На рисунке нормали направлены в разные стороны, поэтому множитель отрицателен.
В многомерном случае линии превращаются в поверхности, однако условие коллинеарности векторов нормалей остается в силе. Таким образом, необходимым условием экстремума является одновременное выполнение двух соотношений:
→− f (→− |
|
λ |
→− |
→− |
|
|
|
X ) |
− |
|
g(X ) = 0 |
— касание с изоцелевой поверхностью; |
|
|
|
|
||||
|
X ) = 0 |
— нахождение на допустимой поверхности. |
||||
g(→− |
|
|||||
Если ограничивающих уравнений не одно, а много, то данные

44 |
Глава 9. |
Теория выпуклого программирования |
|||||||
соотношения должны выполняться для каждого из них: |
|
|
|||||||
→− |
→− |
− |
|
→− |
|
i |
(→− |
(9.21) |
|
|
f (X ) |
λ |
i |
g |
X ) = 0, i = 1, . . . , m, |
||||
|
|
|
|
|
|
||||
→−
gi(X ) = 0, i = 1, . . . , m.
Складывая равенства (9.21) и переобозначая неопределенные
множители через yi = −λmi , получаем необходимые условия экстремума
→− |
|
→− |
m |
→− |
|
|
(→− |
|
|
y |
|
|
|
||||
|
f (X ) + |
i |
i |
g |
i |
X ) = 0; |
(9.22) |
|
|
||||||||
|
|
=1 |
|
|
||||
|
|
i(→− |
|
|
|
|
(9.23) |
|
g |
|
|
|
|
|
|||
X ) = 0, i = 1, . . . , m. |
|
|||||||
Вспоминая определение функции Лагранжа (9.18), замечаем, что выражение (9.22) может быть переписано в виде
→− f (→− |
m |
i→− i |
→− →− |
→− |
m |
i i |
|
→− |
|||||
|
|
y g (X ) = |
|
|
|
i |
|
|
(X ) = |
||||
X ) + |
|
f (X ) + |
y g |
||||||||||
|
i=1 |
|
|
|
|
|
|
|
=1 |
|
|
|
|
= →− L(→− →− |
|
|
|
→− →− |
, . . . , |
∂L(→− →− |
|
= 0, |
|||||
|
|
∂x1 |
|
∂xn |
|
||||||||
|
X , Y ) = |
|
∂L(X , Y ) |
|
|
|
X , Y ) |
|
|
T |
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
что эквивалентно (9.19).
Точно так же в силу линейности функции Лагранжа по yi выражение (9.23) может быть представлено как
X ) = ∂L(→− →− |
= 0, i = 1, . . . , m, |
|
gi(→− |
X , Y ) |
|
|
|
|
∂yi
что эквивалентно (9.20).
П р и м е р. На рис. 9.13 представлена задача минимизации функции двух переменных f (x1, x2) = x21 + (x2 + 1)2 → min при
условии 2x1 + x2 = 2.
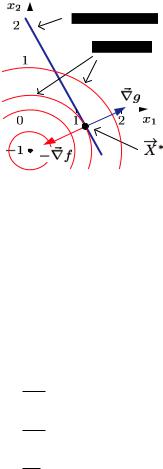
9.3.. Классические задачи оптимизации |
45 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 9.13. Пример условной минимизации с ограничением в виде равенства
Функция Лагранжа для этой задачи
L(x1, x2, y) = x21 + (x2 + 1)2 + y(2x1 + x2 − 2).
Необходимые условия экстремума:
1)∂L = 2x1 + 2y = 0, ∂x1
2)∂L = 2x2 + 2 + y = 0, ∂x2
3)∂L∂y = 2x1 + x2 − 2 = 0.
Решая систему уравнений, получаем x1 = 1.2, x2 = −0.4, y = = −1.2.
Поскольку функции f (x1, x2) и g(x1, x2) выпуклые, то приведенные выше необходимые условия являются достаточными для того, чтобы найденная стационарная точка действительно была точкой условного минимума целевой функции.
46 |
Глава 9. Теория выпуклого программирования |
9.4. Теорема Куна — Таккера
Теорема Куна — Таккера играет ключевую роль в теории выпуклого программирования. Развивая классическую теорию оптимизации с ограничениями в виде равенств, она устанавливает необходимые и достаточные условия оптимальности для общей задачи (9.1):
−→
f (X ) → min,
−→
gi(X ) 0, i = 1, . . . , m,
−→
X 0.
Как и в классической теории, условия оптимальности формулируются с помощью функции Лагранжа (9.18)
L(→− →− →− |
m |
→− |
i i |
||
X , Y ) = f (X ) + |
i |
(X ). |
y g |
||
|
=1 |
|
Для доказательства теоремы нам понадобится условие регулярности (условие Слейтера), которое заключается в том, что допустимая область имеет хотя бы одну внутреннюю точку, т. е.
|
→− |
|
i |
→− |
|
X g |
(X ) < 0, i = 1, . . . , m. |
||
Теорема (Куна — Таккера). При соблюдении условия Слей- |
||||
X |
|
0 |
является оптимальным планом задачи |
|
тера вектор →− |
|
|||
выпуклого программирования тогда и только тогда, когда су-
|
|
|
|
Y |
|
0 |
, такой, что точка |
(X |
Y |
|
|
) |
явля- |
||||||
ществует вектор →− |
|
|
→− |
→− |
|
||||||||||||||
ется с е |
д |
л о |
в о |
й |
|
т о |
ч |
к о й |
функции |
Лагранжа |
|||||||||
в н е о т р и ц а т е л ь н о м октанте, т. е. |
|
|
|
|
|
|
|
||||||||||||
→− |
|
→− |
|
0 |
→− |
→− |
|
→− →− |
) |
|
|
→− →− |
|
). |
|
||||
X |
|
0, Y |
|
L(X |
|
, Y ) |
|
L(X , Y |
|
L(X , Y |
|
|
|||||||

9.4.. Теорема Куна — Таккера |
47 |
→−
Доказательство необходимости. Пусть X — оптимальный
→−
план. Докажем, что существует вектор Y 0, такой, что для
→− →−
(X , Y ) выполняется условие седловой точки.
Построим (m + 1)-мерное (i = 1, . . . , m) евклидово простран-
→−
ство векторов Z = (z0, z1, . . . , zm)T и определим в нем два множества:
|
1 |
= {→− |
| →− |
|
0 : |
|
0 |
|
→− |
|
i |
i |
→− } |
|
|||
K |
|
Z X |
|
z |
|
f (X ), z |
|
g |
(X ) |
, |
|||||||
K2 |
= {→− |
| |
z |
0 |
|
|
(→− |
) |
i |
< |
0} |
. |
|
|
|
|
|
|
|
Z |
|
|
< f X |
|
, z |
|
|
|
|
|
|||||
По способу построения множества K1 и K2 не пересекаются. |
|||||||||||||||||
Множества K1 |
и K2 |
выпуклы. Для K2 это очевидно, так |
|||||||||||||||
как оно является пересечением конечного числа полупространств,
а |
выпуклость |
K1 |
|
доказывается |
|
|
следующим |
|
образом. Пусть |
|||||||||||||||||||||||||||||||||||||
A = (a |
, a |
|
, . . . , a )T |
|
|
B = (b |
, b |
|
, . . . , b )T |
|
— два произвольных |
|||||||||||||||||||||||||||||||||||
→− |
|
0 |
|
|
|
1 |
|
|
m |
|
и →− |
|
|
|
|
0 |
1 |
|
|
|
|
|
|
|
m |
|
|
|||||||||||||||||||
вектора из K1. Тогда по способу построения этого множества най- |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
0, X |
|
|
|
0 |
, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
дутся два вектора →− A |
|
|
|
→− B |
|
|
→− A |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
a0 |
f (→− A |
), a |
i |
|
|
|
i |
|
), |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
g |
(X |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
b |
0 |
f (→− |
|
), b |
|
|
|
|
|
→− |
|
). |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
B |
|
g |
(X |
B |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Образуем произвольную выпуклую комбинацию |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
→− |
|
|
− |
|
→− |
|
|
→− |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
C = (1 |
|
|
|
λ) A |
+ λB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
= (1 − λ)a0 + λb0, . . . , (1 − λ)am + λbm T = (c0, c1, . . . , cm)T |
|||||||||||||||||||||||||||||||||||||||||||||
и покажем, что C K1. Для этого достаточно показать, что су- |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
X |
|
0, |
для которого |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
ществует →− C |
|
|
|
|
|
|
|
→− C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
c0 |
f (→− C |
|
|
i |
|
i |
|
). |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
), c |
|
|
|
|
g |
(X |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
X |
|
= (1 |
− |
λ)X |
|
+ λX |
|
. Этот вектор неотри- |
|||||||||||||||||||||||||||
Возьмем в качестве →− C |
|
|
|
|
|
|
→− A |
|
|
|
|
→− B |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X ) |
|
и |
g |
|
(X ) |
|
|
|
|
|
||||
цателен и для него в силу выпуклости f (→− |
|
|
i |
|
→− |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
f (→− C |
) |
|
(1 |
− |
|
|
|
→− A |
|
|
|
|
|
→− B |
) |
|
(1 |
− |
λ)a |
0 |
+ |
|
0 |
|
0 |
|
|
||||||||||||||||||
|
|
X |
|
|
|
λ)f (X |
|
|
) + λf (X |
|
|
|
|
|
|
|
|
|
λb |
|
|
= c |
, |
|||||||||||||||||||||||
|
g |
(→− |
|
|
) |
|
(1 |
|
|
|
|
|
→− |
|
|
) + |
|
|
|
→− |
|
|
) |
|
(1 |
|
|
|
λ)a + λb |
|
= c |
|
|
|||||||||||||
|
i |
X |
C |
− |
λ)g (X |
A |
λg |
(X |
B |
− |
i |
|
. |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
i |
|
|
i |
|
|||||||||||||||||
48 |
|
Глава 9. |
Теория выпуклого программирования |
|
|||||||||||
Таким образом, −→ |
1 и выпуклость этого множества доказана. |
||||||||||||||
|
|
C |
K |
|
|
|
|
|
|
|
|
|
|
|
|
По теореме об отделимости выпуклых множеств существует |
|||||||||||||||
разделяющая их гиперплоскость, т. е. |
|
|
|
|
|
|
|
||||||||
|
|
→− |
|
K , |
→− |
|
K α |
|
→− |
|
α |
→− . |
|
|
|
α |
|
Z |
1 |
1 |
Z |
2 |
2 →− |
T Z |
1 |
|
T Z |
2 |
(9.24) |
||
→− |
|
|
|
|
|
|
|||||||||
Это неравенство остается справедливым и тогда, когда |
→− 2 лежит |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
на границе K2. При этом, так как координаты векторов в K2 могут принимать сколь угодно большие отрицательные значения,
α |
|
0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
−→ |
|
|
|
Z |
|
Z |
|
граничные точки |
|
|
|
||||
Возьмем в качестве →− |
1 |
и →− |
2 |
|
|
|
|||||||||
Z |
1 |
= f (X ), g |
(X ), . . . , g (X ) |
|
T |
, Z |
= f (X |
), 0, . . . , 0 |
|
T |
|||||
→− |
→− |
1 |
→− |
|
m →− |
|
→− 2 |
→− |
|
|
|||||
и подставим их координаты в (9.24):
m
−→ −→
α0f (X ) + αigi(X )
i=1
X |
). |
(9.25) |
α0f (−→ |
|
Легко убедиться, что α0 (9.25) α0 = 0, получаем
→−X
> 0. В противном случае, положив в
m
−→
αigi(X ) 0,
i=1
что противоречит условию Слейтера. |
|
αi |
|
|
|
|
|
|
|||||||||||
Поделим (9.25) на α0 |
и обозначим y = |
. Таким образом, |
|||||||||||||||||
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
i |
α0 |
|
|
|
|
|
|
||
убедились, что существует вектор →− |
1 |
m |
|
|
|
|
|||||||||||||
= (y |
|
|
T |
|
|
0. Пока- |
|||||||||||||
, . . . , y ) |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
жем, что для него выполняется условие седловой точки. |
|
|
|
||||||||||||||||
Неравенство (9.25) должно выполняться для любых |
→− . В част- |
||||||||||||||||||
ности, положив |
→− |
|
|
→− |
|
|
получаем |
|
|
|
|
X |
|
|
|||||
|
|
, |
|
|
|
|
|
|
|
|
|
||||||||
|
|
X |
= X |
|
|
|
|
|
|
|
|
|
|
|
|
||||
→− |
m |
|
|
|
|
|
|
→− |
|
|
|
|
m |
|
|
→− |
|
|
|
y g (→− |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
f (X ) + |
i |
X |
|
) |
|
f (X ) |
или, сокращая, |
|
|
(X ) |
|
0. |
|||||||
|
i i |
|
|
|
|
|
|
i |
i |
|
|
|
|||||||
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
9.4.. Теорема Куна — Таккера |
|
|
|
|
|
|
|
|
|
|
49 |
|
X |
|
|
|
g (X |
) |
|
0, |
то |
||||
Но так как −→ – план, для которого |
|
i |
−→ |
|
|
|||||||
m |
|
|
|
|
|
|
|
|
|
|
|
|
yi gi(→− |
|
|
|
|
|
|
||||||
i 0 |
0 |
) |
|
|
0. |
|
|
|
|
|
||
|
|
X |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
Отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
(9.26) |
|
yi gi(→− ) = 0 |
. |
|
|
|
||||||||
|
X |
|
|
|
|
|
|
|
|
|||
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
Прибавим (9.26) к правой части (9.25):
−→ |
m |
|
−→ |
m |
yi gi(−→ |
|
|||
f (X ) + |
X ) |
|
f (X |
) + |
yi gi(→− ) |
. |
X |
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|||
Получили правую часть условия седловой точки. |
|
|
|
|
|
|
|||||||||||||||||||||
Теперь докажем левую часть условия седловой точки |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
→− |
|
, Y ) |
|
|
→− |
→− |
|
). |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
L(X |
|
|
|
L(X |
Y |
|
|
|
|
|
|
|
|
|
|
|
||||||||
Действительно, расписав функцию Лагранжа, имеем |
|
|
|
||||||||||||||||||||||||
f (→− |
|
m |
|
|
|
|
|
→− |
|
|
|
→− |
|
|
|
m |
|
|
|
|
|
→− |
|
|
|
||
|
i |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
X |
|
|
0 |
) |
f (X |
|
|
|
y |
g |
(X |
) . |
|
|
|||||||||||||
|
) + |
y |
i |
g |
(X |
|
) + |
|
|
|
|||||||||||||||||
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
i |
|
i |
|
|
|
|
|||||
|
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
i=1 |
|
|
0 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Сокращая f (−→ ), получаем очевидное неравенство. |
|
|
|||||||||||||||||||||||||
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
0, |
Y |
0 |
— |
||||
Доказательство достаточности. Пусть −→ |
−→ |
|
|||||||||||||||||||||||||
седловая точка функции Лагранжа на неотрицательном октанте. |
|||||||||||||||||||||
Покажем, что |
−→ |
— оптимальный план. |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
X |
|
|
|
|
|
|
X |
|
|
0, Y |
0 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
||||||
Распишем условие седловой точки: −→ |
|
−→ |
|
|
|
|
|||||||||||||||
f (→− |
|
|
m |
|
→− |
|
|
|
→− |
m |
|
→− |
|
|
|
→− |
|
|
m |
|
→− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
)+ |
|
(X |
|
) |
|
f (X )+ |
i |
|
(X ) |
|
f (X )+ |
|
|
(X ). |
|||||
X |
|
y g |
|
y |
g |
|
y |
g |
|||||||||||||
|
|
|
i |
i |
|
|
|
|
i |
i |
|
|
|
|
|
i |
i |
|
|||
|
|
|
i=1 |
|
|
|
|
|
|
=1 |
|
|
|
|
|
|
|
i=1 |
|
|
|
