
Методы оптимизации и исследование операций для бакалавров информатики. Часть 2
.pdf
110 |
|
Глава 11. Многомерная оптимизация без ограничений |
|
|||||||||||||||||||
|
Действительно, если обозначить одномерное сечение целевой |
|||||||||||||||||||||
функции |
ϕ(t) = f (X |
|
d |
) |
, то условие минимума этого сечения |
|||||||||||||||||
|
|
→− k + t→− k |
|
|
||||||||||||||||||
записывается в виде уравнения |
|
|
|
|
|
|
|
|
|
|
||||||||||||
∂ϕ(t) |
= →− →− →− →− |
|
|
|
→− →− →− →− →− |
|
|
|
||||||||||||||
|
∂t |
|
|
T f (X |
k |
+ t d |
k |
) d |
|
k |
= |
|
T f (X |
k+1 |
) d |
k |
= d T |
d |
k |
= 0. |
|
|
|
|
|
|
|
|
|
|
|
k+1 |
|
|
|
||||||||||
Равенство нулю скалярного произведения означает ортогональность соседних направлений.
Представьте себе лыжника с нулевой массой, который катится по склону оврага по прямой до тех пор, пока есть наклон, и умеет поворачивать лыжи только под прямым углом. Тогда вместо движения вдоль оврага он будет выписывать зигзаги, переезжая с одного его склона на другой.
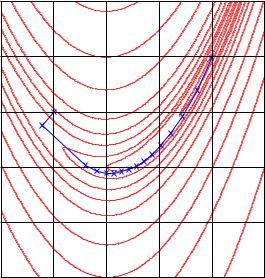
П р и м е р. На рис. 11.7 показаны первые 50 итераций
скорейшего спуска для функции Розенброка из начальной точ-
→−
ки X 0 = (0.5, 0.5)T . Видно, что из-за ортогональности соседних направлений этому методу трудно даются повороты оврагов.
1.5 |
|
200 |
|
|
|
1 |
|
100 |
|
|
|
|
|
|
|
|
|
|
|
50 |
|
|
|
0.5 |
|
20 |
|
|
|
|
|
10 |
|
|
|
|
|
5 |
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
0 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
10 |
|
|
|
|
100 |
20 |
|
|
|
−0.5 |
|
|
200 |
|
|
|
|
100 |
500 |
||
|
200 |
50 |
|
|
|
|
|
|
|
|
|
−1 |
−0.5 |
0 |
0.5 |
1 |
1.5 |
−1 |
Рис. 11.7. Траектория поиска минимума функции Розенброка методом скорейшего спуска. После 50 итераций процесс все еще далек от точки минимума
11.3.. Градиентные методы |
111 |
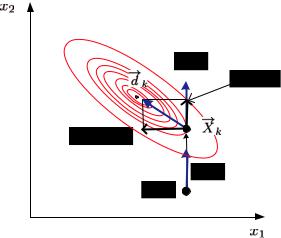
Для того чтобы ускорить движение к минимуму, нужно научить нашего воображаемого лыжника адаптироваться к местности и поворачивать лыжи не под прямым углом, а так, чтобы следую-
щее направление соотносилось с направлением оврага. Подсказать идею нам поможет рис. 11.8, на котором крупным планом показаны два соседних шага градиентного спуска.
Рис. 11.8. Два соседних шага полношагового градиентного метода
−→
Пусть в предыдущей точке X k−1 было выбрано некоторое на-
−→
правление d k−1. Двигаясь в этом направлении и дойдя до мини-
−→
мума, мы пришли в текущую точку X k. Рассмотрим в этой точ-
−→
ке два направления: прежнее d k−1 и направление антиградиента
−→ −→
− f (X k). Как мы установили выше, они ортогональны, движе-
ние по антиградиенту привело бы нас к длительному блужданию
−→
по склокам оврага. «Правильное» направление d k на текущем шаге есть нечто промежуточное между старым направлением и чистым антиградиентом, его можно представить в виде линейной

112 |
Глава 11. Многомерная оптимизация без ограничений |
||||||||||||
комбинации |
|
|
→− |
→− |
|
|
|
−→ |
|
|
|
|
|
|
→− |
|
= |
|
) + β |
|
|
, |
|
|
|||
|
d |
k |
− |
f (X |
k |
k |
d |
k−1 |
(11.3) |
||||
|
|
|
|
|
|
|
|||||||
где βk — некоторый весовой коэффициент. Таким образом, задача коррекции градиента на каждом шаге свелась к выбору соответствующего коэффициента.
Осталось выяснить самое главное — каково должно быть это «правильное» направление? Поскольку для произвольных целевых функций на этот вопрос ответить невозможно, авторы оптимизируют алгоритмы под некоторую известную функцию. Стандартным источником идей является к в а д р а т и ч н а я функция
f (X ) = c T X X T DX |
||
→− |
→− →− +→− |
→− , поскольку любая выпуклая дважды диф- |
ференцируемая функция в локальной области аппроксимируется параболоидом.
Этот подход реализован в методе сопряженных градиентов (conjugate gradients) Флетчера — Ривса [27, с. 98]. Доказано, что если в полношаговом релаксационном методе последовательно использовать так называемые сопряженные направления (conjugate directions), то точный минимум квадратичной функции будет найден не более чем за n шагов. При этом для того чтобы последующее направление было сопряжено предыдущему, весовой коэффициент в выражении (11.3) должен быть равным
|
−→f (−→ |
|
|
|
|
|
||
|
|
X ) |
|
2 |
|
|
||
βk = |
|
|
k |
|
|
. |
||
−→f (−→ |
|
|
) |
|
2 |
|||
|
|
X |
k−1 |
|
|
|||
|
|
|
|
|||||
|
|
|
|
|
||||
Если оптимизируемая функция отличается от квадратичной, то итеративная процедура может продолжаться неограниченно, однако для выпуклых функций сходимость метода сопряженных
градиентов доказана. |
→− |
|
и |
→− |
2 называются сопряжен- |
|||||
Напомним, что два вектора |
1 |
|||||||||
|
d |
|
|
d |
|
D |
d T |
d |
|
= 0, |
ными относительно квадратичной формы |
|
|||||||||
|
, если →− 1 |
D→− |
2 |
|
||||||
то есть понятие сопряженности является обобщением ортогональности.
11.3.. Градиентные методы |
113 |
П р и м е р. Оценим работоспособность метода Флетчера — Ривса на функции Розенброка (рис. 11.9). Видно, что в отличие от метода скорейшего спуска алгоритм достаточно хорошо приспосабливается к искривлению дна оврага и обеспечивает приемлемую точность нахождения минимума за относительно небольшое число шагов.
1.5 |
|
|
|
|
|
1 |
|
|
|
|
|
0.5 |
|
|
|
|
|
0 |
|
|
|
|
|
−0.5 |
|
|
|
|
|
−1 |
−0.5 |
0 |
0.5 |
1 |
1.5 |
−1 |
Рис. 11.9. Траектория поиска минимума функции Розенброка методом Флетчера — Ривса. Проведено
15 итераций. Начальная точка (0.5, 0.5)T , конечная
точка (0.9939, 0.9883)T

114 Глава 11. Многомерная оптимизация без ограничений
11.4.Ньютоновские и квазиньютоновские методы
Для использования многомерных методов второго порядка не-
обходимо иметь аналитические выражения для самой оптимизи- |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
f (→− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→− |
|
|
→− |
|
|
|
|
|
|
|
||||||||
руемой функции |
|
|
X ) |
, вектора градиента |
f (X ) |
и матрицы Гес- |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
се вторых производных H(→− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Классический |
|
|
Данный |
|
метод |
является |
|
|
непосредственным |
||||||||||||||||||||||||||||||||||||||
|
|
обобщением одномерного метода Ньютона на |
|||||||||||||||||||||||||||||||||||||||||||||
метод Ньютона |
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
многомерный случай. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Пусть известно приближенное значение минимума на k-й ите- |
|||||||||||||||||||||||||||||||||||||||||||||||
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (X ) |
|
является дважды дифференци- |
|||||||||||||||||||||||||||||
рации →− k. Если функция |
|
|
→− |
|
|||||||||||||||||||||||||||||||||||||||||||
руемой, то в окрестности точки |
→− k она может быть разложена в |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
многомерный ряд Тейлора и аппроксимирована параболоидом |
|
|
|||||||||||||||||||||||||||||||||||||||||||||
→− |
→− |
|
)+→− |
|
f (→− →− →− |
|
|
|
|
1 |
|
→− →− |
|
|
|
|
→− →− →− |
|
|
||||||||||||||||||||||||||||
Q(X ) = f (X |
k |
|
|
|
T |
|
|
|
X |
k |
)(X |
− |
X |
k |
)+ |
|
(X |
− |
X |
k |
)T H(X |
k |
)(X |
− |
X |
k |
). |
||||||||||||||||||||
|
|
|
|
|
|
2 |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Точка минимума этого параболоида находится из уравнения |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
dQ(→− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
X ) |
|
|
|
|
→− →− |
|
|
|
H(→− →− →− |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
→− |
= |
|
f (X |
k |
) + |
|
|
|
|
X |
k |
)(X |
− |
X |
|
k |
) = 0. |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
dX |
|
|
|
|
|
|
|
|
|
|
|
|
→− k+1: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Отсюда новое приближение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→− |
|
|
|
|
= |
|
→− |
|
|
|
H |
− |
1 |
→− |
|
) |
→− →− |
). |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
X |
k+1 |
|
X |
k |
− |
|
|
(X |
|
|
|
f (X |
k |
|
|
|
(11.4) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
В одномерном случае имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
− |
(→− |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
→− →− |
|
|
) = f (x ), |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
H |
1 |
X |
k |
) = |
|
|
|
|
|
|
, |
|
|
|
|
|
f (X |
k |
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
f (xk) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
и выражение (11.4) естественным образом переходит в (10.2).
Замечание. Если сравнить выражение (11.4) со стандартным правилом вычисления следующего приближения в релаксационном методе
X |
= X |
+t |
d |
→− k+1 |
→− k |
|
k→− k, то можно увидеть, что классический метод Ньютона |

11.4.. Ньютоновские и квазиньютоновские методы |
115 |
на каждой итерации определяет не только ньютоновское направление |
||||||||||||
→− |
|
= |
|
H |
− |
→− |
) |
→− |
→− |
) |
|
t |
d |
k |
− |
|
1(X |
|
f (X |
, но и длину шага |
|||||
|
|
|
|
|
k |
|
k |
k, всегда равную единице. |
||||
Итерационную формулу (11.4) можно получить другим способом, не через квадратичную аппроксимацию целевой функции, а путем численного решения системы нелинейных уравнений.
Пусть система уравнений задана в виде
|
|
|
. .1.(−→ |
|
|
|||||
|
|
|
|
F |
|
X ) = 0, |
|
|
||
|
|
|
|
F |
n |
(→− |
|
|
||
|
|
|
|
|
X ) = 0. |
|
|
|||
|
|
|
|
|
|
|
F (X ) |
= |
||
С использованием |
понятия вектор-функции |
|||||||||
→− →− |
||||||||||
X ), . . . , F (X ) |
T |
эта |
система записывается |
в виде |
од- |
|||||
= F1(−→ |
n −→ |
|
||||||||
|
|
|
|
|
F (X ) = 0. |
|
|
|||
ного векторного уравнения −→ −→ |
|
|
||||||||
|
|
X ) |
дифференцируемы, можно построить |
|||||||
Если функции Fi(−→ |
|
|||||||||
квадратную функциональную матрицу частных производных, называемую матрицей Якоби (якобианом)3:
→− →− →− ∂ F (X )
J(X ) = →−
∂X
→−
∂F1(X )∂x1
= . . .
→−
∂Fn (X )
∂x1
. . .
. . .
. . .
−→
∂F1(X )
∂xn
. . .
−→
∂Fn (X )
∂xn
.
3 |
|
|
|
|
|
|
|
|
|
T |
|
|
F (X ) = F |
(X ), . . . , F |
m |
(X ) |
|
произвольной размер- |
|||
|
Для вектор-функции →− →− |
1 |
→− |
|
→− |
|
||||
|
ности |
m |
матрица Якоби имеет |
размерность m |
× |
n, а транспонированная мат- |
||||
|
|
|
|
|
|
|
|
|
||
рица
T X ) = |
∂−→ −→ |
|
|
∂−→ |
|||
|
|||
J (−→ |
F (X ) |
T |
|
|
|
||
|
X |
|
∂F1 ∂x1
= . . .
∂F1 ∂xn
. . . |
. . . |
|
= →− →− |
. . . |
∂Fm |
|
|
. . . |
∂x1 |
|
|
∂xn |
F (X ) |
||
|
|
|
|
∂Fm
может |
|
быть |
интерпретирована как |
F |
= |
||||
|
градиент вектор-функции →− |
|
|||||||
= (→− F |
|
. . . , |
→− F |
|
). |
Для того чтобы подчеркнуть, что он является матрицей, |
|||
|
1 |
|
|
|
m |
|
|||
стрелка над оператором здесь не ставится. Если F — скалярная функция, то матричный градиент превращается в обычный вектор-столбец.
116 |
Глава 11. |
Многомерная оптимизация без ограничений |
|
|||||||||||
|
Тогда классический ньютоновский итеративный процесс на- |
|||||||||||||
хождения корня уравнения запишется в виде |
|
|
|
|||||||||||
|
→− |
|
= |
−→ |
|
J |
− |
→− →− →− |
), |
|
|
|||
|
X |
k+1 |
|
X |
k − |
|
1(X |
k |
) F (X |
k |
(11.5) |
|||
|
|
|
|
|
|
|
|
|
||||||
при этом определитель матрицы Якоби предполагается отличным от нуля.
−→ −→
Замечание. В одномерном случае, когда F (X ) = f (x), матрица Якоби превращается в простую производную, и итерационная формула (11.5) упрощается до знакомого нам элементарного выражения (10.3) xk+1 = xk − f (xk)/f (xk).
Приведенную здесь процедуру поиска корня векторного уравнения легко приспособить для численного нахождения минимума
функции многих переменных без ограничений, для чего нужно ре- |
||||||||||
→− f (→− |
|
→− |
→− |
f |
|
|
|
|
||
шить уравнение |
X ) = 0. |
В этом случае |
F = |
|
и, как легко |
|||||
видеть, якобиан превращается в гессиан, т. е. |
→− |
= |
( |
→− |
f ) = |
|||||
F |
|
|||||||||
|
|
|
|
|
||||||
= 2f = H. Формула (11.5) естественным образом переходит в (11.4).
Таким образом, существует тесная связь между итеративной
−→
процедурой минимизации функции f (X ), аппроксимируемой па-
раболоидом, и процессом нахождения корня векторного уравне-
−→ −→
ния f (X ) = 0.
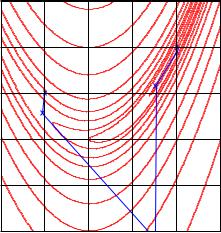
П р и м е р. На рис. 11.10 показана траектория поиска минимума функции Розенброка классическим методом Ньютона. Несмотря на некоторую нерегулярность соседних точек, процесс сошелся очень быстро: для нахождения экстремума с точностью до 10−6 потребовалось всего 5 итераций.
Классический метод Ньютона имеет два очевидных достоинства:
•он хорошо изучен теоретически, прост в реализации и быстро сходится на выпуклых функциях, а при квадратичной целевой функции дает решение всего за один шаг;
11.4.. Ньютоновские и квазиньютоновские методы |
117 |
1.5 |
|
|
|
|
|
1 |
|
|
|
|
|
0.5 |
|
|
|
|
|
0 |
|
|
|
|
|
−0.5 |
|
|
|
|
|
−1 |
−0.5 |
0 |
0.5 |
1 |
1.5 |
−1 |
Рис. 11.10. Траектория поиска минимума функции Розенброка классическим методом Ньютона. Проведено 5 итераций. Начальная точка (0.5, 0.5)T , конечная точка (1, 1)T
•он не использует процедуру одномерной оптимизации вдоль сечения и поэтому не требует грубой локализации экстремума. Однако, как мы увидим далее, это достоинство метода может обернуться его недостатком.
C другой стороны, при практическом использовании метода в реальных условиях обнаруживается ряд недостатков:
•метод весьма чувствителен к сложности оптимизируемой функции. Если рельеф реальной целевой функции сильно изрезан, то квадратичное приближение в большой области становится слишком грубым. Тогда ньютоновское направление на точку минимума аппроксимирующего параболоида может оказаться далеким от направления на истинный экс-

118 Глава 11. Многомерная оптимизация без ограничений
тремум, шаг на единичную длину уводит поиск далеко в сторону;
•если целевая функция во всей области определения невыпукла, то матрица Гессе на некоторой итерации может потерять свойство положительной определенности, в результате ньютоновское направление не будет понижающим.
Указанные обстоятельства могут сделать классический ньютоновский итерационный процесс нестабильным. Иллюстрацией к сказанному является выброс после первой итерации в предыдущем примере (рис. 11.10). К счастью, на следующих итерациях поиск вернулся в область притяжения экстремума и итеративный процесс сошелся, однако на более сложной функции либо при другой начальной точке исход мог бы быть неблагоприятным.
Еще одним существенным недостатком является необходимость аналитического вычисления не только градиента, но и матрицы вторых производных, что может быть весьма затруднительно для сложной целевой функции.
По указанным причинам имеется большое число различных модификаций классического метода Ньютона, образующих обширный класс ньютоноподобных методов (Newton-like methods), которые, сохраняя общую его структуру, пытаются избавиться от указанных недостатков.
Самой очевидной является модификация, при которой используется только ньютоновское направление, а длина ша-
га определяется обычным линейным поиском вдоль выбранного направления:
→− |
|
= |
|
− |
1 |
→− |
|
→− →− |
|
), |
||
d |
k |
− |
H |
(X ) |
|
f (X |
k |
|||||
|
|
|
|
k |
|
|
|
|
||||
k |
|
|
|
|
|
→− k + t→− k |
), |
|||||
t |
= arg min f (X |
|
|
d |
|
|||||||
→− k+1 |
|
t |
|
|
→− k |
|
|
|
||||
|
−→k |
k |
. |
|
|
|||||||
X |
|
|
= X |
|
+ t |
d |
|
|
|
|||
11.4.. Ньютоновские и квазиньютоновские методы |
119 |
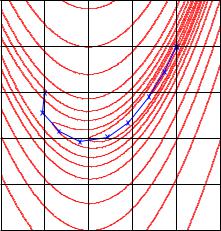
На рис. 11.11 приведена траектория поиска экстремума функции Розенброка методом Ньютона с линейным поиском. Видно, что путь поиска стал более регулярным.
1.5 |
|
|
|
|
|
1 |
|
|
|
|
|
0.5 |
|
|
|
|
|
0 |
|
|
|
|
|
−0.5 |
|
|
|
|
|
−1 |
−0.5 |
0 |
0.5 |
1 |
1.5 |
−1 |
Рис. 11.11. Траектория поиска минимума функции Розенброка ньютоновским методом с линейным поиском, 9 итераций. Начальная и конечная точки те же
Другой подход основан на принудительном ограничении ньютоновской длины шага. Он приводит к методам с ограниченным шагом (restricted step methods), называемых также
методами доверительной области (trust-region methods).
Особенность этих методов в том, что если в обычной ньютоновской процедуре аппроксимация распространяется на все про-
странство, то здесь аппроксимирующая (модельная) квадратич-
→−
ная функция Q(X ) должна достаточно правдоподобно отобра-
→−
жать поведение f (X ) только в окрестности радиуса rk, окружаю-
→−
щей текущую точку X k. Эта окрестность называется доверитель-
