Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Методы оптимизации и исследование операций для бакалавров информатики. Часть 2

.pdf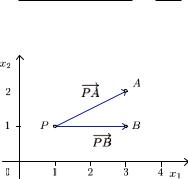

Скачиваний:

187

Добавлен:

26.03.2016

Размер:

7.81 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 273 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Глава 9.

Теория выпуклого программирования

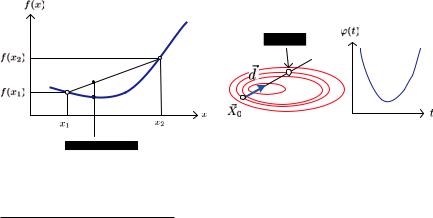
П р и м е р. Вычислим ϕ = AP B (рис. 9.2):

cos ϕ =

−→ −−→

= →−

− →− →− − →−

P A, P B

P , B

−→ · −−→

→− − →− · →−

− →−

P A

P B

(2, 1)(2, 0)T

√

2√

22 + 12

22 + 02

Отсюда ϕ ≈ 26◦.

Рис. 9.2. Иллюстрация к примеру

Проекция точки

Пользуясь

понятием

ортогональности,

гиперплоскость, проходящую чарез точ-

(вектора) на аф-

ку

→− 0

можно определить как геометри-

финное множество

−−−→

ческое место точек →− , таких, что вектор

ортогонален направляющему вектору →−

(рис. 9.3, а).

Следовательно, уравнение гиперплоскости можно записать в

−−−→

a T

→−

) = 0

→−

a T X

X =

−

a T X = b

, где обозначено

виде →−

→−

или →−

b = a

→−

T X

Множество, образованное пересечением m гиперплоскостей в n-мерном пространстве (m < n), называется аффинным множе-

ством или линейным многообразием. Таким образом, аффин-

ное множество задается точкой

→− 0 и направляющими вектора-

, i = 1, . . . , m

−−−→

ортогонален

ми →− i

, причем текущий вектор

каждому из них:

−−−→ =

a T

(→−

→−

) = 0

→−

= b ,

→−

a T X

−

a T X

→− i

или→− i

где i

→− i

9.1.. Евклидово пространство	21

		a)				б)
	Рис. 9.3. Задание гиперплоскости направляющим вектором (а);
		проектирование точки на гиперплоскость (б)
						a T
Если обозначить через Am×n матрицу со строками →− i , через
b	= (b		T
→−		1, . . . , bm)	T	— вектор свободных членов, то аффинное мно-
жество задается уравнением					→−	→− . Этот результат хорошо
					AX =	b

нам известен в алгебраической формулировке.

Как мы знаем, элементы аффинного пространства могут быть интерпретированы как точки и как векторы. Поэтому важное для последующего понятие проекции также может быть описано в

«точечном» и «векторном» вариантах. Начнем с точечного.

−→

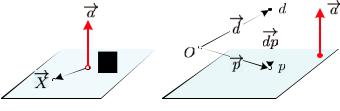
Определение. Проекцией точки d на множество D назы-

вается ближайшая к ней (в смысле введенной евклидовой мет-

→−

рики) точка p этого множества.

Из определения, в частности, следует, что если проектируемая точка находится внутри множества D, то ее проекция совпадает

сней самой.

Вобщем случае операция проектирования сама по себе представляет непростую оптимизационную задачу, однако в простейшем варианте, когда множество D является гиперплоскостью или аффинным множеством, проекцию можно найти аналитически.

Известно, что в элементарной геометрии длина наклонной не может быть менее длины перпендикуляра. Аналогичное свойство

справедливо и для произвольной евклидовой геометрии.

→−

Для начала спроектируем произвольную точку d на одну ги-

22	Глава 9. Теория выпуклого программирования
	a	−→	=
перплоскость, заданную уравнением →−		T X		b	(см. рис. 9.3, б, где
перплоскость, заданную уравнением →−					(см. рис. 9.3, б, где

для наглядности изображены оба способа представления проекти-

руемого объекта и проекции: как точек d, p и как концов соответ-

ствующих радиусов-векторов из начала координат O). Для этого

опустим из →−

на гиперплоскость перпендикуляр

−→, коллинеар-

ный нормальному вектору →− , проекцию →−

будем искать в виде

p = →−

+ −→ =

→− +

→− . Скалярный множитель

найдем из усло-

→−

λ a

(→−

) =

вия принадлежности точки →−

гиперплоскости: →−

λ a

→−

λ = (b

−→)

(

a T a

)

Отсюда

− →−

T d /

→−

→− →− и

→− )

→−

−

−→

(

→− →−

)

→−

(9.2)

= d + (b

a T d / a T a a .

Процедура проектирования (9.2) легко обобщается на многомерный случай. Пусть множество D задано пересечением m ги-

перплоскостей		T X		b	i				Перпендикуляр,
	→− i					, i = 1, . . . , m;		m < n.
	a	→− =
опущенный из точки			→−	на множество			D	, должен быть коллинеа-
			d

рен нормальным векторам всех гиперплоскостей, поэтому проекцию будем искать в виде

p = →− +		m
p = →− +		a λ
→−		i
	d
		=1

→−	→−	где	→−	1		m	)T .
= d	+ AT λ ,		λ	= (λ	, . . . , λ		)T .

Из условия

A p = d

λ = (AAT )

A d )

→−

получаем →−

−

→−

−

(→− −

→−

(AA )−

→−

P →−

→−

(9.3)

d + AT

1( b

A d ) =

d + R ,

где обозначены

P = I

−

AT (AAT )

−

1A, R = AT (AAT ) 1

→−

−

→− .

Квадратная матрица P размерности n × n называется матрицей проектирования. Легко убедиться, что она является симметрической и существует только тогда, когда ранг произведения (Am×nATn×m) равен m, чтобы было возможно выполнить обращение. Для этого матрица Am×n должна иметь ранг, равный числу строк m (полный ранг). Это значит, что среди плоскостей, на которые производится проектирование, не должно быть параллельных.

9.1.. Евклидово пространство

Как видно, выражение (9.3) является многомерным обобщением (9.2).

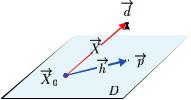
Перейдем к «векторной» интерпретации проекции. Пусть име-

ется вектор →− и аффинное множество

. Возьмем произвольную

точку →− 0 D. Отложив от нее наш вектор, получим точку →−

проекция которой на D есть точка →− (рис. 9.4). Тогда под проек-

цией в е к т о р а →− на

→−

−−→0

мы будем понимать вектор

= X p

То есть при проектировании вектора на аффинное множество D

решается задача разложения произвольного вектора →−

на сумму

X = h

двух ортогональных векторов: проекцию P rD→−

→− и ортого-

нальную составляющую

Ort

→−

−→:

= pd

→−

D→−

+ Ort

D→−

X = P r

X .

Рис. 9.4. Проектирование вектора на аффинное множество

В этом случае, согласно (9.3),

p = P →−

+ →− = (→− →− →−

→− →− →−

→−

d R P X

+ X ) + R = (P X

+ R ) + P X

+ P

X =

совпадает с ней самой

= P rD→−

→−

проекция точки →−

= →−

→−

+ P X .

Отсюда

→−

−−→

→− −

→−

(9.4)

P r

= P X .

= X

= p

Видим, что проекция вектора

→−

не зависит от выбора начальной

−→

точки X 0.

24 Глава 9. Теория выпуклого программирования

Замечание 1. Понятие проекции может быть сформулировано в более общем виде, если воспользоваться определением ортогональных подпространств. Два подпространства евклидова пространства En ортогональны, если каждый вектор первого ортогонален каждому век-

тору второго. Тогда для каждого подпространства A размерности m

(аффинное множество, включающее начало координат, является подпространством) существует его ортогональное дополнение B размерно-

			X		En
сти n − m, такое, что для любого →−					→−	→−
→−	→−	→−	где				B.
X = P rX		+ OrtX ,		P rX		A, OrtX
Замечание 2.	Легко показать, что матрица проектирования P яв-

ляется симметрической и положительно определенной. Симметрия доказывается прямым транспонированием. Для доказательства положи-

X T P X

тельной определенности рассмотрим произведение →−

→− для любого

неотрицательного →− . Тогда

→−

D→−

→−

X T P X = (P r

X + Ort

X )T P r

(9.5)

→−

D→−

→− ·

D→−

2 + 0 >

= P rT

P r

X + OrtT

P r

X =

P r

Замечание 3. Если аффинное множество D задано неособенной квадратной матрицей An×n, то оно является результатом пересечения непараллельных n гиперплоскостей в n-мерном пространстве, т. е. представляет собой точку. Тогда проекция любого вектора на точку равна нулю. Действительно, для квадратной неособенной матрицы существует обратная и (AAT )−1 = (AT )−1A−1, тогда

P= I − AT (AAT )−1A = I − AT (AT )−1A−1A = I − I = 0.

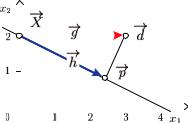
Пр и м е р. Афинное множество в двумерном евклидовом

пространстве представляет собой прямую, заданную уравнением

x	1 + 2x2	= 4 (рис. 9.5). Найдем проекцию вектора	→−	= (3 0)	T	на
x			g	,

данную прямую.

Здесь A = (1, 2), матрица проектирования

P = I − AT (AAT )−1A =

9.2.. Выпуклые функции и их свойства																	25
0	1 − 2				1,			2	2		−1	1, 2			0.4 0.2
= 1	0		1						1		−1		=	0.8		−0.4 .
														−
	h	P g			.	,	−1		. T .	Отложив этот вектор, к приме-
Отсюда →− =		→− = (2			4		−1		2)	Отложив этот вектор, к приме-
		X	= (0	,	2)		T	, получим точку					p = (2.4, 0.8)T .
ру, от точки →−			= (0		2)			, получим точку					→−

Рис. 9.5. Иллюстрация к примеру

9.2. Выпуклые функции и их свойства

Определение.

X )

называ-

Функция многих переменных f (→−

ется выпуклой (строго выпуклой) в выпуклой области D, если

→−

→−1

, X

f [(1

−

→− 1

→− 2

]

(<)(1

−

→− 1

→− 2

λ)X

λX

λ)f (X

) + λf (X

В одномерном случае выпуклость проявляется в том, что функция всегда лежит п о д х о р д о й, соединяющей любые две точки на ее графике (см. рис. 9.6, a). Непосредственно из определения также следует, что линейная функция является выпуклой, хотя и не строго выпуклой.

Замечание. Если знак неравенства в определении выпуклой функции поменять на обратный, получится определение в о г н у т о й функции. Специально рассматривать этот класс функций не имеет

Глобальные

свойства

26	Глава 9. Теория выпуклого программирования

смысла, так как вогнутую функцию легко превратить в выпуклую, умножив ее на −1.

Выпуклые функции обладают рядом полезных свойств. Сначала рассмотрим основные глобальные свойства, не связанные с существованием не-

прерывных частных производных.

Свойство 1 (неравенство Иенсена2). Выпуклая комбина-

→−

ция выпуклых функций выпукла. То есть если f (X ) — выпуклая

функция и αi = 1, αi 0, то

i=1

m	→−

fiαi X

i=1

	m
	αif (→− i
	i	).
	X	).
	=1

Доказательство проводится индукцией по m (см., например, [17, с. 31]).

а)

б)

Рис. 9.6. Свойства выпуклых функций

2Людвиг Иенсен (Jensen, Johan Ludwig; 1859–1925) — датский инженер, сотрудник Копенгагенской телефонной компании. В свободное от работы время занимался математикой. В 1906 г. опубликовал доказательство этого неравенства.

9.2.. Выпуклые функции и их свойства

Свойство 2 (выпуклость множества, заданного выпук-

лой функцией).

X )

— выпуклая функция, то множе-

Если g(→−

ство D =

X : g(X )

} выпуклое.

{→−

→−

→−2

. Это значит, что

Доказательство.

Пусть

→− 1

g(→−

→−

D, x

)

0, g(X

)

X = (1

λ)X

λX

−

Составим выпуклую комбинацию →−

→−

g(→−

−

→− 1

→−

]

X ) = g[(1

λ)X

+ λX

(

) +

g(X

)

(9.6)

−

) g

→−

→− 2

→−

Таким образом

Свойство 3 (выпуклость сечения).

X )

— выпук-

Если f (→−

+ t d )

лая функция, то функция одной переменной ϕ(t) = f (→−

→−

X )

в на-

представляющая собой сечение функции f (→−

из точки →−

правлении

→− , является выпуклой

(см. рис. 9.6, б).

Доказательство.

Данное свойство доказывается непосред-

ственной проверкой:

ϕ[(1

−

1 + λt2] = f (→−

+ [(1

−

λ)t

→−

λ)t

+ λt

] d ) =

→− 0

−

−→

2→−

+ (1

λ)t

+ λt

прибавим и вычтем

→− 0

= f (X

d ) =

λX

→−

−

→−

+ (1

λ)t

+ λt

2−→

→−

0 −

→− 0

) =

= f (X

+ λX

λX

= f [(1

−

→− 0

+ t

→−

→− 0

+ t

→−

λ)(X

d ) + λ(X

d )]

X )

— выпуклая функция

так как f (→−

→−

+ t

→−

+ t

→−

λ)ϕ(t

) + λϕ(t

−

λ)f (X

d ) + λf (X

d ) = (1

−

Следовательно, ϕ(t) — выпуклая функция.

28 Глава 9. Теория выпуклого программирования

На первый взгляд свойство выпуклости не связано с непрерывностью. Однако на самом деле оно оказывается столь сильным, что из него следуют важные локальные свойства.

−→

Свойство 4 (непрерывность). Выпуклая функция f (X ), определенная на выпуклом множестве D, непрерывна в каждой внутренней точке этого множества и имеет производные по

		d
любому направлению →− :
∂f (X )			1		X + t d )			f (X )
	→−	=	1	lim	f (−→	−→	−	−→	.
		=	d	lim		t			.
	d		d	t +0		t
	d		→
	∂→−		→

Нетривиальное доказательство этого факта можно найти в
[24, с. 105].
	Замечание. Из приведенного свой-
	ства отнюдь не следует дифференцируе-
	мость	функции,	то	есть	существование
	н е п р е р ы в н ы х				X )	во
				производных f (−→
	всех внутренних точках области определения.
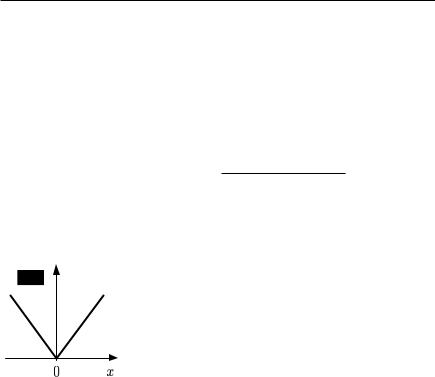
	На рис. 9.7 в качестве				примера приведе-
	на функция одной переменной f (x) = \|x\|.
	Эта функция с очевидностью непрерывна и
Рис. 9.7.	выпукла на всей числовой оси, дифференци-
	руема во всех точках, кроме нуля. В нуле она
непрерывна, имеет производные по направлению слева и справа,
однако эти производные не совпадают, следовательно, в данной
точке функция недифференцируема.

Экстремальные

Поскольку выпуклые функции интересуют нас

свойства

не сами по себе, а с точки зрения оптимизации, необходимо прежде всего уточнить поня-

тие экстремума.

Пусть задача заключается в нахождении минимума или максимума целевой функции на множестве допустимых значений D:

→−

f (X ) → min (max).

→−

X D

9.2.. Выпуклые функции и их свойства

Для определенности впредь будем иметь в виду задачу минимизации, поскольку максимизация достигается сменой знака у целевой функции.

Глобальным решением или точкой глобального минимума на-

зывается вектор →− , такой, что

)

f (X ).

(9.7)

→−

f (→−

→−

Локальным

решением

или

точкой

локального

миниму-

ма называется

вектор

что

существует некото-

→− , такой,

рая ε-окрестность точки →− , образованная пересечением шара

X :

} с допустимой областью

= R

ε ∩

Rε = {→−

→− −

→−

в которой

)

f (X ).

(9.8)

−→

f (−→

−→

В зависимости от вида неравенств в (9.7) и (9.8) говорят о строгих или нестрогих минимумах в глобальном или локальном смысле. Всякий глобальный минимум является локальным, но не

наоборот. Для глобального решения часто используется обозначе-

ние →− = arg min f (→− )

→−

Свойство 5. Любой локальный минимум выпуклой функции

X )

на выпуклом множестве

является глобальным.

f (→−

Доказательство (от противного).

Предположим, что точ-

ка локального оптимума

→−

не является глобальной. Тогда

найдется →−

, такая, что

f (→−

→−

) < f (X

Рассмотрим точки вида

→− = (1

−

)

λ X

+ λX ,

Поскольку D — выпуклое множество, то X D. Далее, в силу

→−

выпуклости функции f (X ),

<<< < Предыдущая 1 23 / 273 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.05.2015337.94 Кб84методичка, задачи микро.pdf
#
08.08.2019142.85 Кб3Методичка.Контрольная.Задачи..doc
#
11.11.2019401.41 Кб2Методичка_Микро_Лит_ТГУ.doc
#
26.11.2019506.88 Кб14Методологические проблемы клинической психологи...doc
#
02.05.2019118.27 Кб2Методы обучения рисованию в России.doc
#
26.03.20167.81 Mб187Методы оптимизации и исследование операций для бакалавров информатики. Часть 2.pdf
#
03.09.201979.36 Кб2методы проведения маркетинговых исследований.doc
#
30.05.201598.82 Кб26Методы психологии развития.doc
#
12.11.20191.96 Mб32МЕТОДЫ_РЕШЕНИЯ_ЗНЛП.doc
#
14.09.201935.16 Кб5Микробиология на госы.docx
#
10.11.2019233.98 Кб2Микроэкономика Лекции Г..А. Тарунина.doc