Методы оптимизации и исследование операций для бакалавров информатики. Часть 2

−→

мы будем обозначать вектор производных по X .

необходимые условия оптимальности (уравнения Куна — Таккера) для классической задачи минимизации с неограниченными по знаку переменными и ограничениями-равенствами:

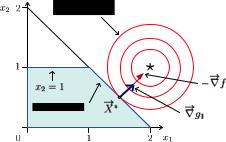
П р и м е р. Вернемся к примеру на с. 45 c минимизацией функции f (x1, x2) = x21 + (x2 + 1)2 → min при условии 2x1 + x2 = 2 и добавим еще одно «полуклассическое» ограничение x2 > 0, так

что допустимая область теперь представляет собой полупрямую (рис. 9.16).

Рис. 9.16. Пример условной минимизации с полуклассическими ограничениями

Прежде чем сформулировать необходимые условия экстремума, заметим, что, хотя условие Слейтера для данной задачи не выполняется (прямая не имеет внутренних точек), ограничивающая функция является линейной, поэтому теорема Куна — Таккера и следующие из нее дифференциальные условия сохраняют силу.

Функция Лагранжа для этой задачи остается прежней:

L(x1, x2, y) = x21 + (x2 + 1)2 + y(2x1 + x2 − 2).

Начнем выписывать необходимые условия экстремума. Поскольку переменная x1 неограничена по знаку, условия «a», «б», «в» для нее превращаются в одно условие равенства нулю частной производной. Для переменной x2 потребуются все три условия, в итоге получаем четыре соотношения:

1)∂L = 2x1 + 2y = 0, ∂x1

2)∂L = 2x2 + 2 + y 0, ∂x2

3)x2 ∂L = x2(2x2 + 2 + y) = 0, ∂x2

4)x2 0.

Так как единственное ограничение имеет вид равенства, соответствующие ему условия «г», «д», «е» превращаются в одно:

5)∂L∂y = 2x1 + x2 − 2 = 0.

Поскольку функции f (x1, x2) и g(x1, x2) выпуклые, эти необходимые условия условного минимума являются и достаточными.

Для нахождения решения следует решить систему нелинейных уравнений «1», «3», «5» и отобрать те решения, которые удовлетворяют неравенствам «2» и «4».

Эта система эквивалентна двум линейным системам:

Решая «а», получаем x1 = 1, x2 = 0, y = −1. Легко видеть,

что это решение удовлетворяет неравенствам «2» и «4», следова-

→−

тельно, точка X = (1, 0)T есть искомое решение условной экстремальной задачи (см. рис. 9.16).

Поскольку линейные функции являются выпуклыми, то с формальной точки зрения задача линейного программирования является частным случаем общей задачи выпук-

лого программирования. Интересно посмотреть, во что превращаются в данном случае дифференциальные условия Куна — Таккера.

Пусть задача линейного программирования задана в канонической форме (в развернутой и матричной записи):

что можно представить более компактно, используя матричные обозначения:

Компоненты градиента функции Лагранжа получаются дифференцированием (9.36):

C учетом этого требование (9.40) означает, что удовлетворя-

→−

ющий условиям Куна — Таккера вектор Y должен быть планом двойственной задачи линейного программирования, для которого выполняется условие (9.41), т. е.

Таким образом, мы показали, что в случае линейного программирования теорема Куна — Таккера эквивалентна фундаментальной Первой теореме двойственности, а двойственные переменные

— это множители Лагранжа.

9.7.Квадратичное программирование. Метод Вулфа

C точки зрения чистой математики теория Куна — Таккера исчерпывает проблему выпуклого программирования. Для любой конкретной задачи следует составить условия Куна — Таккера и решить получающуюся систему уравнений и неравенств. К сожалению, на практике все обстоит значительно сложнее. Эта система является нелинейной, ее решение представляет не менее сложную задачу, чем непосредственный поиск экстремума.

Счастливым исключением является задача квадратичного программирования, которую, применяя теорию Куна — Таккера, ценой существенного повышения размерности удается свести к задаче линейного программирования и найти т о ч н о е решение за конечное число шагов.

Таким образом, задача поиска оптимального решения задачи квадратичного программирования сводится к нахождению

н е о т р и ц а т е л ь н о г о решения системы линейных урав-

−→ −→ −→ −→

нений (9.47) – (9.48) относительно переменных X , Y , u , v , при

этом должно соблюдаться дополнительное комбинаторное усло-

переменных, при этом комбинаторное условие (9.49) говорит о том, что m + n переменных равны нулю. Следовательно, нужно найти такое неотрицательное частное решение системы m + n линейных уравнений, в котором имеется ровно m + n ненулевых переменных, то есть неотрицательное б а з и с н о е решение. При этом в базисном решении не должны одновременно появляться сопряженные переменные, то есть переменные с одноименными индексами xj , vj и yi, vi.

Нахождение такого решения можно произвести методом искусственного базиса. Для этого введем искусственные переменные

−→

W 1 = (w1, . . . , wn),

−→

W 2 = (wn+1, . . . , wn+m)

и поставим задачу минимизации суммы искусственных переменных

n+m

wi → min

i=1

Решаем эту задачу обычным симплексным методом, с тем лишь ограничением, что в базисе не должны одновременно появляться сопряженные переменные xj , vj и yi, ui.

П р и м е р. Имеется простейшая задача минимизации квадратичной функции при линейных ограничениях (рис. 9.17):

Рис. 9.17. Пример задачи квадратичного программирования

Для применения метода Вулфа приведем задачу к стандартному виду 9.42, для чего раскроем скобки в целевой функции:

f (x1, x2) = (x1 − 2)2 + (x2 − 1)2 = −4x1 − 2x2 + x21 + x22 + 5 → min .

Выпишем участвующие в задаче матрицы и векторы:

Таким образом, всего имеется 3m+3n = 12 переменных, m+n = 4 уравнения.

Задача линейного программирования с искусственными пере-

Исходная симплексная таблица приведена в табл. 9.1.

Для решения потребовалось четыре итерации симплексного метода (показаны включаемые в базис и исключаемые переменные):