
Методы оптимизации и исследование операций для бакалавров информатики. Часть 2
.pdf
90 |
Глава 10. Одномерная оптимизация |
|
|
|
ных сооружениях, например в храме Парфе- |
||
|
нон в Афинах. |
||
|
Леонардо да Винчи считал, что идеаль- |
||
|
ные пропорции человеческого тела определя- |
||
|
ются золотым отношением длин меньшей и |
||
|
большей частей, приблизительно равным 38:62 |
||
|
(рис. 10.10). |
||
|
Числа Фибоначчи названы по имени сред- |
||
|
невекового математика Леонардо Пизан- |
||
|
ского (1180–1240), известного под прозвищем |
||
|
Фибоначчи (от ит. «Figlio Buono Nato Ci — |
||
Рис. 10.10. |
хороший сын родился»). В своем главном тру- |
||
де «Книга абака» (1202) он впервые система- |
|||
Идеальные |
|||
тически изложил для европейцев достижения |
|||
пропорции |
|||
арабской математики, а также ввел в рассмотрение возвратную последовательность.
Метод Ньютона — Рафсона имеет долгую историю. Первый вариант, пригодный для приближенного вычисления корней полиномов, был разработан Ньютоном в 1669 г. и впервые опубликован в 1685 г. не им самим, а в виде приложения к
«Алгебре» Джона Уоллиса (Wallis, John; 1616– 1703). В 1690 г. Джозеф Рафсон (Raphson,
Joseph; 1649–1715) предложил упрощенный вариант метода, пригодный опять-таки для полиномов. Он же перевел на английский язык
некоторые книги Ньютона, написанные на ла-
Фибоначчи
тыни.
Выдающийся английский математик следующего века Томас Симпсон (Simpson, Thomas; 1710–1761), оставивший свое имя в «формуле Симпсона» численного интегрирования, в работе, вышедшей в 1740 г., обобщил метод Ньютона — Рафсона на произвольные функции и придал ему современный вид.
Глава 11
Многомерная оптимизация без ограничений
В этой главе мы сделаем еще один шаг к решению общей задачи математического программирования. Опираясь на общую идею релаксационных методов и имея в запасе арсенал алго-
ритмов одномерной оптимизации, попытаемся найти экстремум
→−
функции многих переменных f (X ) = f (x1, . . . , xn) без учета ограничений. Проблему оптимизации с ограничениями откладываем до следующей главы.
11.1. Релаксационные методы оптимизации
Существует множество приближенных итерационных методов оптимизации без ограничений, называемых релаксационными (to
relax – снижать, расслаблять) потому, что в процессе их рабо- |
||||||
ты, начиная с некотором образом выбранной исходной точки |
→− 0, |
|||||
образуется последовательность точек →− |
1, →−2 |
→− k |
→− k+1 |
|
X |
|
, . . . |
, в |
|||||
X |
X |
, . . . , X |
, X |
|
||
которой каждая последующая имеет лучшее (меньшее) значение
−→ −→
целевой функции: f (X k+1) < f (X k). Если задача имеет решение
и целевая функция ограничена, то в пределе эта последователь- |
|||
ность должна сходиться к точке минимума: |
→− k → |
→− |
. |
|
X |
X |
|

92 Глава 11. Многомерная оптимизация без ограничений
Для того чтобы прочувствовать проблемы и идеи релаксационных методов, можно воспользоваться такой аналогией. Представим себе путника, оказавшегося ночью в горной местности и желающего прийти в точку с минимальной высотой. Склоны гор ровные, нет ни камней, ни трещин, движение возможно во всех направлениях, однако из-за полной темноты путник не видит всего рельефа и не может определить истинное направление на цель, он полагается только на ощущения в ближайшей окрестности ме-
ста своего нахождения1. Если путник находится в текущей точке
→−
X k и хочет сделать очередной шаг для того, чтобы спуститься ниже, то он должен определить:
→−
• направление шага d k,
• величину шага tk в выбранном направлении,
причем сделать это таким образом, что в новой точке, определяемой по правилу
→− k+1 |
→− k |
k |
→− k |
, |
X |
= X |
+ t |
d |
значение целевой функции уменьшится.
Подавляющее большинство релаксационных методов относится к классу методов, основанных на линейном поиске (linesearch methods). В них первичным является выбор направления, после чего производится движение в выбранном направлении. Эти методы развивались на протяжении нескольких столетий (см. исторические замечания в конце главы), хорошо себя зарекомендовали на практике и включены во все пакеты прикладных программ оптимизации. По этой причине все внимание в дальнейшем будет уделено именно им.
1Некоторые авторы, например [25], предпочитают пользоваться противоположной аналогией, формулируя задачу не на минимум, а на максимум. Тогда ущелья превращаются в хребты, а цель поиска состоит в восхождении на высочайшую вершину.
11.1.. Релаксационные методы оптимизации |
93 |
|
|
Общая схема |
Каждая k-я итерация спуска (k = 0, 1, 2, . . . ) |
||
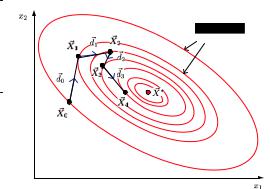
определяется следующим алгоритмом (рис. 11.1). |
|||
Рис. 11.1. Схема работы метода спуска на примере минимизации выпуклой функции двух переменных
→−
1. В текущей точке X k, k = 0, 1, 2, . . . определяется некото-
→−
рое направление движения d k, обладающее тем свойством, что, двигаясь в данном направлении, можно хоть ненамного уменьшить значение целевой функции. Любое такое направ-
ление называется понижающим (descending) или прогрес-
→−
сивным. Сечение целевой функции f (X ) вдоль выбранного
направления является одномерной функцией от величины
→− →−
перемещения t : ϕ(t) = f (X k + t d k).
2. |
Определяется величина шага tk |
в выбранном прогрессивном |
||||||
|
|
X |
|
|
) < f (X |
). |
||
|
направлении, такая, что f (−→k+1 |
|
−→k |
|
||||
3. |
Происходит спуск в точку, являющуюся исходной для следу- |
|||||||
|
ющей итерации: →− k+1 |
→− k |
+ t |
k→− k |
. |
|
||
|
X |
= X |
|
d |
|
|||
4. |
Проверяется критерий остановки алгоритма. |
|||||||

94 Глава 11. Многомерная оптимизация без ограничений
Из приведенного описания ясно, что релаксационные методы спуска могут различаться:
•по способу выбора понижающего направления,
•по способу выбора длины шага,
•по критерию остановки итерационного процесса.
Даже если ограничения отсутствуют, проблема выбора понижающего направления совсем не проста. С одной стороны, она определяется той априорной информацией, которой мы располагаем об оптимизируемой функции. Если, например,
функция задана аналитически простой формулой, то легко вычислить все ее производные. Вполне логично в этом случае двигаться по направлению наибольшей крутизны, то есть антиградиенту. Если же информация о производных недоступна, применяются другие подходы.
С другой стороны, необходимо учитывать особенности целевой функции. Существует множество очень трудных для оптимизации, так называемых овражных функций, рельеф которых изрезан глубокими оврагами с крутыми стенами. Как мы увидим в дальнейшем, движение по антиградиенту в этом случае является далеко не оптимальным, приходится изыскивать иные способы выбора прогрессивного направления.
Наличие ограничений, особенно нелинейных, резко усложняет задачу оптимизации, поскольку не все направления движения из исходной точки являются возможными (feasible), а только те, по
которым можно хоть немного продвинуться, не выходя за преде-
→−
лы области допустимых значений X . Продолжая аналогию с горами, можно представить, что разрешенная область ограничена забором. Если путник касается забора, то возможными направлениями будут только те, которые ведут внутрь области или хотя бы вдоль забора.
11.1.. Релаксационные методы оптимизации |
95 |
По этой причине рассмотрение соответствующих методов обычно начинают после того, как изучены методы оптимизации без учета ограничений. Для этого есть все основания, так как исходную задачу с ограничениями часто можно свести к задаче без ограничений. Мы не будем отходить от этой традиции и отложим оптимизацию с ограничениями до гл. 12.
С точки зрения определения длины шага все методы спуска делятся на две группы. В методах
с малым (дробным) шагом величина шага спуска в выбранном направлении является предустановленным параметром алгоритма: tk = h. То есть путник, сделав шажок фиксированной длины, заново определяет направление своего следующего шага, даже если возможность уменьшения целевой функции за счет движения в прежнем направлении не исчерпана.
Следует заметить, что фиксирование длины шага, впрочем как и любых других численных параметров алгоритма, несет определенную опасность. Для одних условий величина шага может оказаться слишком малой, в результате число итераций получится непомерно большим, а для других, наоборот, она будет слишком велика, и, сделав шаг установленной длины, можно проскочить точку минимума функции ϕ(t). Поэтому при конструировании рабочего алгоритма с малым шагом следует предусмотреть подстройку длины шага (см., например, [17, с. 163]).
В методах с большим (полным) шагом движение по лучу, ис-
→−
ходящему из X k в направлении dk, осуществляется до тех пор, пока не будет достигнут минимум целевой функции в данном направлении. При этом длина шага находится из соотношения
|
X |
+ t d |
). |
tk = arg min ϕ(t) = arg min f (→− k |
→− k |
|
|
t |
t |
|
|
Таким образом, в полношаговых методах спуска задача оптимизации функции многих переменных сводится к последовательности задач одномерного (линейного) поиска минимума.

96 Глава 11. Многомерная оптимизация без ограничений
Критерий
Подобно всем итеративным методам, релаксаци-
остановки
онные алгоритмы могут работать бесконечно, их остановка производится принудительно по дости-
жении заданной точности вычислений. В зависимости от конкретных условий из итерационного цикла можно выходить по любому из следующих критериев остановки (stopping criterion).
По выполнению условий первого порядка. Как мы знаем (см. c. 39), равенство нулю градиента целевой функции является необходимым, а в случае выпуклой функции — и достаточным условием экстремума. Практически эта проверка реализуется сле-
→−
дующим образом. В текущей точке X k вычисляется мера опти-
мальности первого порядка (first order optimality measure), и если она менее установленного допуска (tolerance) ε, например 10−6, то условие считается выполненным. В качестве меры можно взять евклидову норму вектора градиента, однако чаще используется условие с так называемой бесконечной нормой:
→− k ∞ |
1 j n ( |
∂xj |
( < ε. |
|
|
|
( |
X ) |
( |
f (X ) |
= max |
( |
∂f (→− k |
( |
|
|
( |
|
( |
( (
Данный критерий является самым логичным, однако он требует знания производных целевой функции, в связи с этим широко используются другие критерии, основанные на сравнении двух соседних точек в итерационном процессе.
По малости смещения текущей точки. Возможны два варианта данного критерия: по абсолютному либо относительному
смещению. В первом случае оценивается евклидова норма векто- |
||||
ра →− k+1 |
− →− k |
< ε, |
во втором для измерения относительного |
|
X |
X |
|
|
|
смещения часто используют отношение |
||||
|
|
|
→− k+1 |
− −→k < ε, |
|
|
|
X |
X |
−→
1 + X k
где единица в знаменателе исключает возможность деления на нуль.
11.1.. Релаксационные методы оптимизации |
97 |
По малости изменения целевой функции. Аналогично, критерием выхода по абсолютному изменению целевой функции
|
|
|
|
|
|
|
X |
|
) |
− |
f (X ) |
| |
< ε |
, а по |
||
является выполнение неравенства |f (→− k+1 |
|
→− k |
|
|||||||||||||
относительному — соотношения |
|
|
|
|
|
|
|
|
|
|
|
|||||
| |
−→k+1 |
) |
− f (−→k |
| |
< ε. |
|
|
|
|
|
||||||
|
|
f (X |
|
X |
) |
|
|
|
|
|
|
|
|
|
||
|
|
1 |
+ |f (−→k |
| |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
X ) |
|
|
|
|
|
|
|
|
|
|
|
|
По малости производной по направлению. Еще одним критерием может служить оценка производной по направлению в текущей точке. Используя ее определение (см. с. 30), можно записать конечно-разностное приближение
|
→− |
= lim |
→− |
→− |
− |
→− |
|
f (→− k+1 |
) |
− |
→− k |
. |
||||
∂f (X ) |
|
|
|
f (X |
+ t d ) |
|
f (X ) |
≈ |
X |
|
f (X |
) |
|
|||
∂ |
→− |
t |
→ |
0 |
|
|
→− |
|
|
→− k+1 − |
→− k |
|
|
|||
|
d |
|
|
|
|
|
t d |
|
|
|
X |
|
|
X |
|
|
Если абсолютная величина этого выражения менее установленного порога, работа алгоритма завершается.
По объему вычислений. В качестве «предохранительного клапана», защищающего итеративный процесс от зацикливания или недопустимо большого времени работы, могут служить прямые ограничения на количество итераций либо на число вычислений целевой функции.
В практических алгоритмах указанные критерии используются независимо либо в комбинации друг с другом.
Основанием для классификации является, как и в одномерном случае, доступная априорная информация о целевой функции (табл. 11.1). В литературе описано много
различных методов, в таблице мы указали и в дальнейшем будем рассматривать только самые простые и типичные. Как мы отмечали выше (см. с. 94), они могут отличаться друг от друга способом выбора понижающего (прогрессивного) направления,

98 Глава 11. Многомерная оптимизация без ограничений
Таблица 11.1. Классификация релаксационных методов
|
|
X ) |
Метод |
Группа |
Что известно о f (→− |
методов |
|||
|
|
|
|
|
|
|
|
||
Выпуклая |
Метод покоординатного |
Методы |
||
|
|
|
спуска (Гаусса — Зайделя) |
нулевого |
|
|
|
Метод многогранника (симп- |
порядка |
|
|
|
лексный) Нелдера — Мида |
|
|
|
|
Поиск по образцу (метод кон- |
|
|
|
|
фигураций Хука — Дживса) |
|
Выпуклая, |
Метод скорейшего спуска |
Методы |
||
дифференцируемая, |
Метод сопряженных градиен- |
первого |
||
известен градиент |
тов (Флетчера — Ривса) |
порядка |
||
→− |
→− |
|
|
|
|
|
|
||
|
f (X ) |
|
Квазиньютоновские методы |
|
|
|
|
||
Выпуклая, дважды |
Классический метод Ньютона |
Методы |
||
дифференцируемая, |
и его модификации |
второго |
||
известны градиент |
|
порядка |
||
→− |
→− |
|
|
|
|
f (X ) |
и матрица |
|
|
|
|
|
||
|
H(X ) |
|
|
|
Гессе |
→− |
|
|
|
величиной шага и критерием окончания поиска. Из этих трех параметров главным является способ выбора направления, так выбор длины шага чаще всего ведется поиском минимума функции в выбранном направлении, а критерий остановки не имеет принципиального значения.
11.2. Методы нулевого порядка
Метод покоорди- |
Метод циклического покоординатного спус- |
|
ка (coordinatewise descend), носящий имя |
||
натного спуска |
||
Гаусса — Зайделя2, является классическим |
||
|
2Зайдель (Зейдель) (Philipp Ludwig von Seidel; 1821–1896) — немецкий математик и астроном. Труды по теории рядов и других бесконечных форм. В

11.2.. Методы нулевого порядка |
99 |
полношаговым методом оптимизации, не требующим знания производных.
Направления одномерной оптимизации на каждой итерации выбираются параллельными координатным осям, то есть изменяется только одна переменная. При этом для одномерной оптимизации можно использовать любой метод нулевого порядка: золотое сечение или метод парабол. После того, как найден минимум по первой переменной, осуществляется поиск по второй, и так до последней, затем цикл повторяется, пока не будет достигнута требуемая точность.
Символически покоординатный спуск описывается следующими соотношениями:
d |
k {→− 1 →− 2 |
|
|
|
→− n} |
|
|
|||
→− |
|
e , e , . . . , e |
, |
|
||||||
t |
k |
= arg min f (→− k |
|
→− k |
), |
|||||
|
|
t |
|
X |
+ t d |
|
||||
→− k+1 |
|
|
→− k |
|
|
|
||||
→− k |
|
k |
. |
|
|
|||||
X |
|
= X |
+ t |
d |
|
|
|
|||
Доказательство сходимости метода для выпуклых функций приведено в [17, с. 194].
Главным достоинством метода является его предельная простота. Весь вопрос в том, какова скорость сходимости, и здесь мы сталкиваемся с проблемой, общей для всех методов многомерной оптимизации.
Рассмотрим поведение метода Гаусса — Зайделя на простом примере минимизации квадратичной функции двух переменных в двух различающихся ситуациях (см. рис. 11.2).
На рис. 11.2, а целевая функция взята из примера на с. 35. Матрица D квадратичной формы является хорошо обусловленной, ее число обусловленности cond(D) ≈ 6. Рельеф такой функции похож на яму, склоны которой имеют приблизительно равную крутизну во всех направлениях. В этом случае покоординатный
астрономии известен своими исследованиями яркости звезд.
