
Методы оптимизации и исследование операций для бакалавров информатики. Часть 2
.pdf30 |
|
|
Глава 9. Теория выпуклого программирования |
|||||||||||||||||||||
f (→− |
− |
λ)X |
|
|
] |
|
(1 |
− |
|
|
|
|
|
|
|
|
) < |
|
|
|
|
|||
X ) = f [(1 |
|
|
+ λX |
|
|
λ)f (X |
) + λf (X |
|
|
|
|
|||||||||||||
< |
так какf (→− ) |
|
|
(→− ) |
|
|
< |
(1 − |
) |
( |
X |
) + |
( |
X |
) = |
( |
X |
) |
. |
|||||
|
|
X |
< f X |
|
|
|
|
λ |
f |
|
|
λf |
|
|
f |
|
||||||||
→−
Но это противоречит утверждению о том, что X→− — точка ло-
кального минимума, так как при 0 < λ < ε точка X находится в
→−
ε-окрестности точки X .
Доказанное свойство имеет фундаментальное значение для выпуклой оптимизации, поскольку позволяет заменить глобальные условия минимума локальными, основанными на дифференциальных свойствах функций в предположении, что все частные производные существуют и непрерывны.
Дифференциальные
свойства
Вектор частных производных функции
X ) |
X |
многих переменных f (→− |
в точке →− на- |
зывается градиентом и обозначается как
→− f (→− |
|
→− |
, . . . , |
∂f (→− |
|
. |
∂x1 |
∂xn |
|||||
X ) = |
|
∂f (X ) |
|
X ) |
|
T |
|
|
|
|
|
|
Из курса математического анализа (см., например, [15, с. 19]) известно, что вектор градиента указывает направление скорейше-
X ) |
|
X |
. Противоположный ему |
го увеличения функции f (→− |
в точке →− |
||
→− f (→− |
|
|
|
по направлению вектор − |
X ) |
называется антиградиентом, |
|
|
|||
он определяет направление скорейшего убывания. Скорость из-
−→
менения f (X ) по направлению, задаваемому произвольным век-
−→
тором d , называется производной по направлению (directional
derivative) и может быть выражена как проекция градиента на выбранное направление:
∂f (→− |
= lim |
→− |
→− |
|
− |
→− |
= |
|
|
|
|
|
|
|
|
||||
X ) |
|
|
|
f (X |
+ t d ) |
|
f (X ) |
|
|
|
|
|
|
|
|
|
|||
∂→− |
t |
→ |
0 |
|
→− |
|
|
|
|
|
|
|
|
|
|
|
|||
d |
|
|
|
|
|
t d |
|
→− f (→− |
→− |
|
|
→− |
→− |
→− |
|
||||
|
= pr d |
→− f (→− |
|
|
X ), d |
= |
|
|
T f (X ) d |
(9.9) |
|||||||||
|
|
|
|
|
|
|
. |
||||||||||||
|
|
→− |
X ) = |
|
|
→− |
|
|
|
|
|
→− |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
d |
|
|
|
|

9.2.. Выпуклые функции и их свойства |
31 |
Вектор градиента имеет еще одну важную геометрическую интерпретацию. Если задана функция нескольких переменных
X ) |
, то уравнение |
f (X ) = |
const при различных значениях const |
f (→− |
→− |
задает семейство поверхностей равных значений (равного уровня)
|
|
|
|
|
X ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
||
функции f (→− |
в пространстве переменных →− . Если фиксировать |
|||||||||||||||||||||||||||||
|
|
X |
|
, то уравнение |
f (X ) = f (X |
|
|
) |
определит поверхность |
|||||||||||||||||||||
точку →− |
0 |
|
|
→− |
|
→− 0 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→− |
|
|
|
→− |
→− |
|
) |
|
|
равного уровня, проходящую через точку |
X |
0. Тогда |
f (X |
0 |
есть |
|||||||||||||||||||||||||
вектор внешней нормали к этой поверхности в точке |
→− 0, а урав- |
|||||||||||||||||||||||||||||
нение касательной гиперплоскости к ней в точке →− |
X |
|
|
|
||||||||||||||||||||||||||
0 |
имеет вид |
|||||||||||||||||||||||||||||
→− f (→− |
|
|
→− |
|
→− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
||
|
T |
X )(X |
|
X ) = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
0 |
|
|
− |
|
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
X ) |
выпукла и дифференцируема на вы- |
|||||||||||||||||||||||
|
|
Свойство 6. Если f (→− |
||||||||||||||||||||||||||||
пуклом множестве, то для любых двух точек →− →− 0 этого мно- |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X , X |
|
|
|
|
|
||
жества |
|
|
|
→− |
|
|
→− |
|
) + |
→− |
→− →− →− |
|
). |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
f (X ) |
f (X |
0 |
|
T f (X |
0 |
)(X |
− |
X |
0 |
|
|
|
(9.10) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
В одномерном случае это свойство совершенно прозрачно: вы-
пуклая функция располагается над касательной прямой в любой точке (рис. 9.8): f (x1) f (x0) + f (x0)(x − x0).
Рис. 9.8. Иллюстрация к свойству 6
Доказательство.
любого 0 λ 0
−→ f [(1 − λ)X
По определению выпуклой функции для
0 + |
→− |
] |
|
(1 |
− |
→− |
0 |
→− |
|
λX |
|
|
λ)f (X |
|
) + λf (X ). |

32 |
Глава 9. Теория выпуклого программирования |
Это неравенство может быть записано по-другому:
→− |
0 |
→− − →− |
0 |
)] |
|
→− |
0) + λ[f (→− |
− |
→− |
0 |
)]. |
(9.11) |
f [X |
|
+ λ(X X |
|
|
f (X |
X ) |
|
f (X |
|
|
Введем обозначения для направления и длины шага:
d |
= |
→− |
− |
→− |
0 , |
|
→− |
|
X |
X |
|
|
|
|
|
|
|
|
||
|
|
→− |
− |
→− |
0 |
|
|
|
X |
|
X |
|
|
→− →−
t = λ X − X 0 .
С учетом этого (9.11) перепишется в виде
|
|
f (→− |
→− |
|
→− |
0 |
) |
|
|
|
|
|
|
→− − →− |
0 |
X |
+ t d ) |
− |
f (X |
|
|
→− |
− |
→− |
0 |
). |
|
|
t |
|
|
|
|||||||||
X X |
|
|
|
|
|
|
|
|
f (X ) |
|
f (X |
|
−→
Переходя к пределу при t → +0 и учитывая, что d = 1, слева получаем производную по направлению:
−→ −→ −→ ∂f (X 0)X − X 0 −→
∂ d
X ) |
− |
f (X |
0 |
). |
(9.12) |
f (→− |
→− |
|
Но производная по направлению равна проекции градиента на данное направление:
∂f (→− |
|
) |
|
→− |
→− |
|
→− |
|
→− |
→− →− →− |
|
) |
|
|
||||||
X |
0 |
= |
|
T f (X |
0 |
) d |
= |
|
|
T f (X |
0 |
)(X |
− |
X |
0 |
. |
(9.13) |
|||
∂→− |
|
|
|
|
|
|
|
|
|
→− − →− 0 |
|
|
|
|||||||
d |
|
|
|
|
d |
|
|
|
|
|
|
X |
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Подставляя (9.13) в (9.12), получаем (9.10).
Переходим к частным производным второго порядка. Матрица вторых частных производных (если они существуют), вычислен-
ных в точке |
→− |
, называется матрицей Гессе |
3 |
или гессианом и |
|
X |
|
|
|
обозначается как
3Людвиг Гессе (Hesse, Ludwig Otto; 1811–1874) — немецкий математик, изучавший эту матрицу. Сам Гессе пользовался термином «функциональные детерминанты».
9.2.. Выпуклые функции и их свойства |
|
|
|
|
|
|
|
|
33 |
|
|||||||||
|
|
|
2 |
|
|
|
|
|
f (→− |
|
∂ |
|
→− |
|
|
|
|
||
|
|
|
|
|
∂x1 |
∂x1 . . . |
|
∂x1 |
∂xn |
|
|
|
|||||||
|
|
|
|
|
|
|
∂2 |
|
X ) |
|
|
2f |
(X ) |
|
|
|
|
||
X ) = |
|
2f (X ) = |
∂ f (→− ) |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂→− →− |
∂2 |
|
X |
|
∂ |
2f (X ) |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
H(→− |
|
→− |
|
X |
|
|
|
|
f (→− ) |
|
|
→− |
|
. |
|
|
|||
|
|
|
|
|
|
|
|
|
. . . . . . . . . |
|
|
|
|
||||||
|
|
|
X ∂X |
|
|
|
|
|
. . . |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
∂xn∂x1 |
|
∂xn∂xn |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X ) |
вы- |
||
Свойство 7. Дважды дифференцируемая функция f (→− |
|
||||||||||||||||||
пукла (строго выпукла) в окрестности точки →− |
тогда и только |
||||||||||||||||||
|
|
|
|
|
|
X ) |
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
неотрицательно (положи- |
|||||||||||||
тогда, когда ее матрица Гессе H(→− |
|||||||||||||||||||
тельно) определена в этой точке.
Доказательство не приводим, его можно найти в любом учебнике по математическому анализу.
Напомним, что положительная (неотрицательная) определен- |
|||||||
ность матрицы A = (aij ) означает, что для любого вектора →− |
|||||||
|
|
i |
|
|
|
|
Z |
Z T A Z = |
a |
|
z |
z |
|
||
квадратичная форма →− |
→− |
j |
ij |
i |
|
j строго положитель- |
|
на (неотрицательна). Для проверки матрицы на положительную определенность существует критерий Сильвестра: матрица является положительно (неотрицательно) определенной, если все ее угловые миноры положительны (неотрицательны).
Квадратичная
Исключительно важную роль в нелинейном
функция
программировании играет многомерная квадратичная функция, общий вид которой вклю-
чает квадратичную, линейную составляющие и свободный член:
|
n n |
n |
|
1 |
|
|
|
|
X |
d x x |
+ c x |
+a = |
X T DX + c T X +a, |
(9.14) |
|||
|
||||||||
Q(→− ) = |
ij i j |
j j |
|
2 →− |
→− →− →− |
|||
|
i=1 j=1 |
i=1 |
|
|
|
|
|
|
где D — симметричная квадратная матрица (матрица квадратичной формы). Градиент и матрица Гессе для квадратичной функ-
ции равны соответственно |
+ |
|
H(→− ) = 2 |
|
→− f (→− ) = →− |
→− |
|||
|
X DX |
|
|
|
|
|
c , X D. |
||

34 Глава 9. Теория выпуклого программирования
Таким образом, выпуклость квадратичной функции целиком определяется определенностью матрицы D.
Можно показать (см., например, [16, с. 214]), что путем переноса начала координат в точку
−→ = −1 −1−→
X 2 D c
можно избавиться от линейной составляющей, и в новой системе |
||||||||||||||||||||||
координат →− функция (9.14) превращается в простую квадра- |
||||||||||||||||||||||
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X : |
тичную форму со свободным членом a , не зависящим от →− |
||||||||||||||||||||||
→− |
|
) = |
→− |
|
→− |
|
+ |
|
|
|
|
|
|
|
= |
|
1 |
c |
|
|
c . |
|
Q(X |
|
|
X |
|
T DX |
|
|
|
, |
где |
|
|
|
− |
4 |
→− |
T d |
− |
→− |
|||
|
|
|
|
|
a |
|
|
a a |
|
|
|
|
1 |
|
||||||||
Далее, поворотом координатных осей полученную квадратич- |
||||||||||||||||||||||
ную форму можно привести к каноническому виду |
|
|
||||||||||||||||||||
|
|
|
|
Q(−→ |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
X |
) = |
|
λ |
(x |
|
)2 + a |
, |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
где λi — собственные числа матрицы D.
Форма поверхности равных значений целевой функции (в двумерном случае — изоцелевых линий) целиком определяется опре-
деленностью матрицы D и ее собственными числами.
→−
Если матрица положительно определена, то Q(X ) выпукла, все собственные числа вещественны и положительны. Поверхности равных уровней такой функции представляют собой много-
мерные концентрические эллипсоиды (в двумерном случае — эл-
→− →−
липсы) с центром в X , являющейся точкой минимума Q(X ). Размеры главных осей эллипсоидов определяются собствен-
ными числами M = λ1 λ2 · · · λn = m. Таким образом, степень сплющенности эллипсоидов определяется отношением наибольшего и наименьшего собственных чисел матрицы D, которое называется числом обусловленности (conditional number) матрицы и обозначается cond(D). Если cond(D) = Mm ≈ 1, то поверхности равных уровней близки к сферическим, если же cond(H) 1,

9.2.. Выпуклые функции и их свойства |
35 |
то матрица относится к классу плохо обусловленных, вследствие чего эллипсоиды равных уровней сильно вытянуты. Как мы увидим в дальнейшем, плохая обусловленность существенно усложняет задачу минимизации квадратичной функции.
Направления главных осей эллипсоидов определяются собственными векторами, соответствующими собственным числам, при этом наибольшей полуоси соответствует наименьшее собственное число и наоборот.
П р и м е р 1. Пусть квадратичная функция двух переменных задана выражением
Q(x1, x2) = x21 + 3x22 + 2x1x2 − 4x1 − 6x2 + 4.5.
Отсюда
1 |
3 |
, |
→− |
= |
−6 |
D = 1 |
1 |
|
c |
|
4 , a = 4.5. |
−
Угловые миноры матрицы D положительны:
1 > 0, |
1 3 |
> 0, |
||
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
следовательно, функция Q(x1, x2) строго выпукла во всей бесконечной области определения. Для нахождения собственных чисел составим характеристическое уравнение
I = 1 − λD − λ
1
3 |
1 |
λ |
= λ2 − 4λ + 2 = 0. |
|
− |
|
|
Решая его, получаем M = λ1 = 3.4142; m = λ2 = 0.5858. Число
обусловленности cond(D) ≈ 5.83, следовательно, отношение боль-
ших и малых полуосей эллипсов равно cond(D) ≈ 2.41.
На рис. 9.9 изображено семейство изолиний данной квадратичной функции, при этом координаты общего центра эллипсов

36 |
|
|
Глава 9. |
Теория выпуклого программирования |
|||||||
находятся в точке |
|
→− |
= −2 |
1 |
3 |
|
−6 0.5 |
||||
→− |
|
|
−2 D− |
−1 |
|||||||
X |
|
= |
1 |
|
1 |
c |
1 |
1 |
1 |
4 = 1.5 . |
|
|
|
|
|
|
|
|
|
||||
−
Рис. 9.9. Пример выпуклой квадратичной функции
Для нахождения направлений главных осей эллипсов определим собственные векторы матрицы D, соответствующие найденным ранее собственным числам. Воспользовавшись процедурой вычисления собственных чисел матрицы из пакета MATLAB, получаем
→− |
1 |
→− |
2 |
= ( |
− |
0.9239, 0.3827)T . |
v |
|
= (0.3827, 0.9239)T , v |
|
|
Углы между направлениями главных осей эллипсоидов и любой из координатных осей можно измерить, применив формулу для

9.2.. Выпуклые функции и их свойства |
37 |
вычисления углов между двумя векторами в евклидовом про-
странстве: |
|
cos ϕ = |
→− →− . |
|
|
|
||||||
|
|
|
|
|
|
X , Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→− · →− |
|
|
|
|
||
|
→− |
→− |
|
−→ |
|
X |
Y |
|
|
|
= →− |
1 = |
Если положить |
1, |
= →− 1 |
и учесть, что →− |
1 |
||||||||
|
X |
= v |
|
Y |
|
e |
|
|
v |
|
e |
|
= 1, получим выражение для угла между малой полуосью эллипса (ей соответствует б´ольшее собственное значение λ1) и осью абсцисс
cos ϕ = →− |
1 |
→−1 |
0 |
v |
|
, e |
= (0.3827, 0.9239) 1 = 0.3827. |
Отсюда ϕ = 67, 5◦ (см. рис. 9.9). Заметим, что для случая двух переменных угол наклона эллипса можно определить непосред-
ственно по матрице D квадратичной формы: tg 2ϕ = 2d12
d11 − d22
[18, с. 66].
Продолжим пример и посмотрим, как ведет себя градиент.
→−
Возьмем точку X 0 = (−3, 0.5)T . Градиент функции в этой точке равен
|
|
|
→− |
|
|
|
−6 1 |
3 0.5 −9 |
||||||
→− Q(→− |
0 |
) = c |
→− |
0 |
= |
4 |
+ 2 |
1 |
1 |
− |
3 |
= |
9 |
|
|
X |
|
+ 2DX |
|
− |
|
|
|
|
− |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
и направлен, как видно, влево и вниз. Соответственно вектор антиградиента направлен вправо и вверх (из-за недостатка места длины векторов на рисунке уменьшены).
Построим касательную к изолинии в данной точке. Ее уравнение имеет вид
→− Q(X0)(→− − →− 0) = −9 |
T |
x2 |
|
|
0.5 |
|
|||
T |
X |
X |
9 |
|
x1 |
+ 3 |
= 0. |
||
|
− |
|
|
− |
|
||||
|
|
|
|
|
|
|
|||
Выполняя скалярное произведение, получаем уравнение прямой −9x1 − 9x2 − 22.5 = 0. Если привести его к виду уравнения в
38 |
Глава 9. Теория выпуклого программирования |
|
|||||||
отрезках, получим |
x1 |
|
+ |
x2 |
|
= 1. То есть касательная отсекает |
|||
−2.5 |
−2.5 |
||||||||
|
|
|
|
|
|||||
на осях координат x1, x2 отрезки −2.5 и −2.5, что мы и видим на |
|||||||||
рис. 9.9. |
|
|
|
|
|
|
|
|
|
П р и м е р 2. В качестве контрпримера рассмотрим квадратичную функцию Q(x1, x2) = x21 +3x22 +4x1x2, заданную матрицей
D = |
1 |
2 |
. |
|
2 |
3 |
|||
|
|
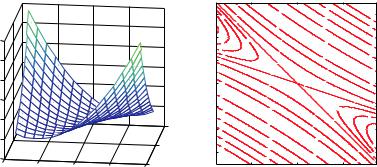
Данная матрица не удовлетворяет критерию Сильвестра и имеет собственные числа λ1 = −0.24, λ2 = 4.23. Как следствие, функция невыпукла, ее изоцелевые линии представляют семей-
ство гипербол с общим центром в начале координат (рис. 9.10).
→−
Точка X = (0, 0)T является седловой точкой (saddle point), так как в ней функция Q(x1, x2) имеет минимум по одному направлению и максимум по другому.
100
80
60
40
20
5
0 |
|
|
|
|
|
−20 |
|
|
|
|
0 |
|
|
|
|
|
|
4 |
2 |
0 |
−2 |
−4 |
−5 |
3
2
1
0
−1
−2
−3
− 2
−3 −2 −1 0 2
6 10
20
30
40 50
60 70
6
2 0
− 1
−2
20
10 6 2 0
0 2 6 10
20
30
40 50
|
|
|
50 |
|
|
|
40 |
|
|
|
30 |
|
|
|
20 |
|
|
|
10 |
|
|
|
6 |
|
0 |
|
2 |
|
|
|
|
|
|
|
1 |
|
|
2 |
− |
|
|
0 |
|
|
|
6 |
|
|
|
|
|
|
|
10 |
|
|
|
20 |
|
0 |
|
|
2 |
0
2 6
70 60
50 40
30 20
10 6 2
−2
− 3 − −2 1 0
Рис. 9.10. Трехмерный рельеф и изолинии невыпуклой квадратичной функции двух переменных

9.3.. Классические задачи оптимизации |
39 |
9.3. Классические задачи оптимизации
Прежде чем исследовать общую задачу выпуклого программирования (9.1), рассмотрим ее упрощенные варианты, изучаемые в классическом курсе математического анализа. Все участвующие в постановке задач функции предполагаются при этом г л а д к и м и, т. е. непрерывно дифференцируемыми.
В простейшем случае ограничения на оптимизируемые переменные отсутствуют, и мы имеем задачу минимизации функции мно-
гих переменных в неограниченной области
−→
f (X ) = f (x1, . . . , xn) → min, 0 < xj < ∞, j = 1, . . . , n.
Вкурсе математического анализа доказывается [15, с. 31], что
не о б х о д и м ы м условием локального минимума является равенство нулю всех частных производных (теорема Ферма):
→−
∂f (X ) = 0, j = 1, . . . , n. (9.15) ∂xj
Это равенство является условием первого порядка (first order condition) и может быть записано в компактной векторной форме
→− f (→− |
|
|
|
X ) = 0. |
(9.16) |
|
||
Точки →−X , удовлетворяющие условию первого порядка, называются стационарными. Однако стационарность не обязательно связана с минимумом, стационарными являются точки как минимума, так и максимума, а также точки перегиба одномерных функций или седловые точки в многомерном случае.
Д о с т а т о ч н ы м условием локального минимума является
→−
положительная определенность матрицы Гессе H(X ) в стационарной точке. Этот факт представляется достаточно очевидным, так
