
Методы оптимизации и исследование операций для бакалавров информатики. Часть 2
.pdf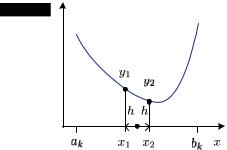
80 |
Глава 10. Одномерная оптимизация |
10.3. Минимизация унимодальных функций
Дихотомия
По-видимому, самым простым методом нулевого
порядка является метод половинного деления или метод дихотомии (рис. 10.3).
Рис. 10.3. Метод дихотомии
Работа алгоритма начинается с отрезка [a0, b0], найденного методом грубой локализации экстремума, после чего следуют итерации (k = 0, 1, 2, . . . ). На каждой итерации функция вычисляется в двух точках, равноотстоящих от середины текущего промежутка:
x1 = |
ak + bk |
− h, x2 = |
ak + bk |
+ h, |
2 |
2 |
где h — параметр алгоритма. Далее переход к следующей итера-
ции (k := k + 1) с новыми границами промежутка: если y1 < y2, то ak+1 := ak, bk+1 := x2, в противном случае ak+1 := x1, bk+1 := bk.
Выход из алгоритма по условию bk − ak < ε.
Этот простейший алгоритм имеет два серьезных недостатка. Во-первых, в нем имеется предустановленный параметр h, определяющий разнос точек измерения функции, этот параметр следует согласовывать с длиной промежутка.
Во-вторых, алгоритм неоптимален с точки зрения трудоемкости. Под трудоемкостью алгоритма одномерной оптимизации обычно понимают число измерений функции, необходимое для достижения заданной точности локализации экстремума.

10.3.. Минимизация унимодальных функций |
81 |
Если абстрагироваться от величины h, то можно считать, что на каждой итерации ценой двух измерений происходит уменьшение отрезка в два раза. Если обозначить относительную точность локализации экстремума через δ = (bk − ak)/(b0 − a0), то δ = 2−n2 , где n — число измерений, необходимое для достижения заданной относительной точности. Отсюда для дихотомии
2 |
|
nD = −log 2 log δ. |
(10.1) |
По указанным причинам метод дихотомии на практике применять нецелесообразно, вместо него можно использовать столь же простой, но лишенный указанных недостатков метод золотого сечения.
Золотое
Напомним, что золотым сечением отрезка называет-
сечение
ся такое его разбиение на две неравные части, при котором отношение длины меньшей части к большей
равно отношению большей части к длине всего отрезка (рис. 10.4).
Чтобы найти это золотое отношение |
||||||||||||||||
(обозначим его λ), будем считать длину все- |
|
|
|
|||||||||||||
|
|
|
||||||||||||||
го отрезка единичной. Тогда |
|
|
|
|
|
|
||||||||||
|
|
|
1 − λ |
|
|
|
|
|
|
|
|
|
|
Рис. 10.4. Золотое |
||
|
|
|
= |
λ |
, |
|
|
|
|
сечение |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
λ |
1 |
|
|
|
|
|
|
|
|
|
|||
|
λ2 = 1 |
|
λ, λ = |
√ |
|
− 1 |
|
0.618. |
|
|
|
|
||||
откуда |
− |
5 |
≈ |
Приведенное на рис. 10.4 |
||||||||||||
|
|
|
2 |
|
|
|||||||||||
сечение назовем правым, потому что точка сечения ближе к правому краю отрезка, однако существует симметричное ему левое золотое сечение.
Золотое отношение тесно связано с последовательностью чисел Фибоначчи {1, 1, 2, 3, 5, 8, 13, . . . }, которые определяются рекуррентным соотношением
F0 = F1 = 1, Fk = Fk−1 + Fk−2, k 2.
82 |
Глава 10. Одномерная оптимизация |
Легко установить [6], что
lim Fk−1 = λ.
k→∞ Fk
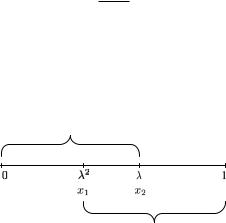
Для наших целей золотое сечение представляет интерес по следующей причине. Возьмем отрезок, для простоты единичный, и поместим на него две точки x1 и x2, производящие его левое и правое золотые сечения (рис. 10.5).
Точка 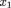 делает золотое сечение этого отрезка
делает золотое сечение этого отрезка
Точка 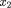 делает золотое сечение этого отрезка
делает золотое сечение этого отрезка
Рис. 10.5. Особенность золотого сечения
Можно показать (мы предлагаем сделать это самостоятельно), что в этом случае левая точка x1 производит правое золотое се-
чение отрезка [0, x2], а правая точка x2 — левое золотое сечение отрезка [x1, 1].
В этом и состоит изюминка метода золотого сечения. Как и при дихотомии, на k-м шаге на отрезке [ak, bk] производятся два измерения целевой функции в точках
x1 = ak + λ2(bk − ak), x2 = λ(bk − ak).
Если f (x1) < f (x2), то в качестве нового отрезка берется [ak+1 = ak, bk+1 = x2], в противном случае [ak+1 = x1, bk+1 = bk], причем в обоих случаях одно измерение для следующей итерации у ж е и м е е т с я.
Таким образом, хотя уменьшение длины отрезка на каждой итерации происходит не в два, а в 1/λ ≈ 1, 618 раза, зато, если не считать начальную итерацию, это происходит ценой всего

10.4.. Метод парабол |
83 |
одного нового измерения целевой функции. То есть относительная точность, достигаемая за n измерений, равна δ = λn, откуда log δ = n log λ, и число измерений целевой функции, необходимое для достижения заданной точности при золотом сечении, равно
log δ nG = log λ .
Выигрыш в числе измерений по сравнению с дихотомией состав-
ляет |
log λ |
|||
|
nD |
|||
|
|
= 2 |
|
≈ 1.388 раза. |
|
nG |
log 2 |
||
Возникает естественный вопрос: существуют ли еще бо- |
||||
лее эффективные с |
точки зрения числа измерений мето- |
|||
ды нулевого порядка для унимодальных функций? Доказано (см., например, [24, с. 56]), что при заранее неизвестном, потенциально бесконечном числе итераций метод золотого сечения является наилучшим из возможных. Если же число итераций k заранее фиксировано, то теоретически возможно (хотя практически нецелесообразно) незначительное увеличение эффективности путем использования самих чисел Фибоначчи. При этом точки измерения целевой функции на первой итерации делят отрезок (если считать его единичным) в пропорции
x1 = Fk−2 , x2 = Fk−1 , Fk Fk
на следующей итерации k уменьшается на единицу и т. д. За счет рекуррентного свойства последовательности Фибоначчи одно измерение при переходе к следующей итерации будет сохраняться. Такой метод называется поиском Фибоначчи. Нетрудно видеть, что при k → ∞ он превращается в золотое сечение.
10.4. Метод парабол
Если априорно известно, что целевая функция не только унимодальна, но и выпукла, эту информацию можно использовать
84 |
Глава 10. Одномерная оптимизация |
для ускорения поиска экстремума. Самым простым методом нулевого порядка для выпуклых функций является метод парабол.
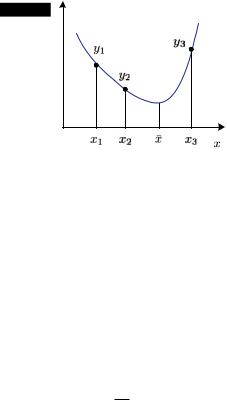
Пусть известно, что f (x) – выпуклая функция и некоторым способом (грубой локализацией экстремума) определена выпуклая тройка точек, не лежащих на одной прямой (рис. 10.6):
Рис. 10.6. Иллюстрация метода парабол
x1 < x2 < x3, y1 y2 y3.
Тогда через эти три точки можно провести интерполирующую параболу
y = ax2 + bx + c.
Точку минимума x¯ параболы можно принять за приближенное значение экстремума, она находится из уравнения y (x) = 0 :
2ax + b = 0, x¯ = −2ba .
Коэффициенты a и b определяются из решения системы уравнений (они линейны относительно переменных a, b, c)
ax21 + bx1 + c = y1, ax22 + bx2 + c = y2, ax23 + bx3 + c = y3.
10.5.. Метод касательных |
|
|
|
|
85 |
||
Решая систему по правилу Крамера, получаем |
|||||||
|
|
|
x12 |
y1 |
1 |
|
|
|
|
|
|
|
|||
|
|
|
x22 |
y2 |
1 |
|
|
x¯ = − |
1 |
|
x32 |
y3 |
1 |
|
. |
2 |
|
y1 |
x1 |
1 |
|
||
|
|
||||||
|
|
|
y2 |
x2 |
1 |
|
|
|
|
|
y3 |
x3 |
1 |
|
|
Легко проверить, что x1 x¯ x3, и y(¯x) y2.
Если x¯ < x2, то в качестве следующей выпуклой тройки точек берутся {x1, x,¯ x2}, в противном случае {x2, x,¯ x3}.
10.5. Метод касательных
Все рассмотренные методы относились к методам нулевого порядка, так как не использовали информацию о производной оптимизируемой функции.
Описываемый ниже метод является методом первого порядка, т. е. предполагает знание не только самой функции f (x), но также ее первой производной f (x). Идея метода состоит в аппроксимации выпуклой функции отрезками касательных.
Если f (x) выпукла и дифференцируема, то уравнение касательной в точке xk имеет вид
y = gk(x) = f (xk) + f (xk)(x − xk).
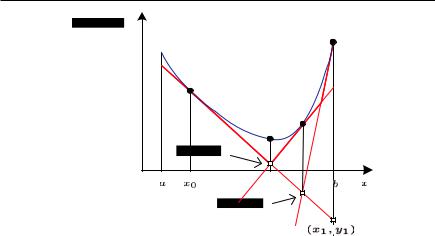
Предположим, что минимум целевой функции грубо локализован на промежутке [a, b] (см. рис. 10.7).
На н а ч а л ь н о й итерации возьмем произвольную начальную точку x0 [a, b] и построим касательную
y = g0(x) = f (x0) + f (x0)(x − x0).
86 |
Глава 10. Одномерная оптимизация |
|
Рис. 10.7. Иллюстрация метода касательных |
Далее сформулируем вспомогательную задачу линейного программирования (задачу 0) с двумя переменными x, y:
y → min, y g0(x), a x b.
Геометрически это означает, что, не выходя по абсциссе за пределы отрезка [a, b], мы ищем точку с минимальной ординатой, расположенную н а д касательной к точке x0. Разумеется, минимум достигается на одном из концов промежутка [a, b], в нашем случае на правом. Координаты этой точки обозначим x1, y1, переходим к следующей итерации.
На п е р в о й итерации построим касательную к целевой функции в точке x1
y = g1(x) = f (x1) + f (x1)(x − x1),
добавим ее к ограничениям задачи 0 и построим задачу 1:
y → min,
10.6.. Метод Ньютона |
87 |
yg0(x),
yg1(x),
a x b.
Решение этой задачи дает точку x2, y2. Она имеет наименьшую ординату среди точек, расположенных над обеими касательными.
На в т о р о й итерации строим касательную y = g2(x) в точке x2 и, добавляя ограничение y g2(x) к условиям задачи 1, получаем задачу 2. Решая ее, получаем точку x3, y3 и т. д.
Таким образом, на каждой итерации, добавляя новую касательную, мы уточняем аппроксимацию целевой функции отрезками касательных и приближаемся к точке ее минимума.
Разумеется, при реализации метода для решения вспомогательных задач линейного программирования нет нужды привлекать тяжелую артиллерию симплексного метода, можно придумать какой-нибудь простой алгоритм перебора точек пересечения касательных (студенты факультета информатики делают это с легкостью). Тем не менее в целом метод выглядит тяжеловесным, мы привели его не для практического использования, а для демонстрации того, как может быть использована дополнительная информация о производной.
10.6. Метод Ньютона
Метод Ньютона (см. исторические замечания в конце главы) является классическим методом второго порядка, так как предполагает знание не только самой функции f (x), но также ее первой
ивторой производных f (x), f (x).
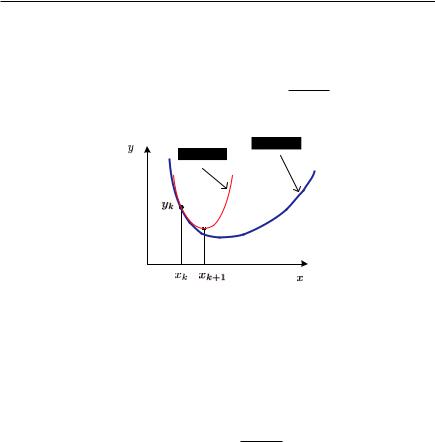
Вотличие от всех предыдущих, данный метод не требует грубой локализации экстремума на отрезке [a0, b0]. Пусть приближенное значение минимума на k-й итерации равно xk (см. рис. 10.8). Идея метода состоит в аппроксимации минимизируемой функции параболой y = g(x), построенной по одной точке xk. Это возможно, так как известны значение самой функции, направление каса-
88 Глава 10. Одномерная оптимизация
тельной (первая производная) и кривизна (вторая производная). Уравнение аппроксимирующей параболы в точке xk при этом имеет вид
y = g(x) = f (xk) + f (xk)(x − xk) + f (xk) (x − xk)2. 2
В качестве следующего k + 1 приближенного значения экстре-
Рис. 10.8. Иллюстрация метода Ньютона. Целевая функция f (x), аппроксимирующая парабола g(x)
мума принимаем точку минимума аппроксимирующей параболы, которая находится из уравнения g (x) = 0, откуда
f (xk) + f (xk)(x − xk) = 0,
xk+1 = xk − f (xk) . (10.2) f (xk)
Доказательство сходимости метода Ньютона и оценка скорости сходимости для выпуклых функций имеется в любом продвинутом учебнике по методам оптимизации, например [24, с. 219].
Замечание. Методом Ньютона в вычислительной математике обычно называют простейшую итеративную процедуру решения уравнения f (x) = 0, когда нелинейная функция аппроксимируется касательной, и следующее приближение для корня вычисляется по геометрически очевидной формуле (рис. 10.9)
xk+1 = xk − |
f (xk) |
= xk − |
f (xk) |
(10.3) |
|
|
|
. |
|||
tgϕ |
f (xk) |
||||

10.7.. Исторические замечания |
89 |
Рис. 10.9. Решение нелинейного уравнения методом Ньютона
Однако, поскольку задача нахождения экстремума функции f (x) эквивалентна нахождению корня уравнения f (x) = 0, итеративная процедура остается той же, только саму функцию следует заменить ее первой производной, а первую производную — второй. Получилась формула (10.2).
Подводя итог методам одномерной оптимизации, следует сказать, что с практической точки зрения наиболее удобными являются методы нулевого порядка (золотого сечения и парабол). Методы первого и второго порядков применимы лишь тогда, когда оптимизируемая функция имеет достаточно простую аналитическую форму, чтобы производные могли быть получены в явном виде и вычислялись отдельными подпрограммами. Это сделать тем более непросто, когда задача одномерной оптимизации является вспомогательной для вычисления длины шага в релаксационном алгоритме.
10.7. Исторические замечания
Золотое отношение известно с античных времен, древние математики придавали ему мистический смысл. Установлено, что пропорции, определяемые золотым отношением, наиболее приятны для глаза, они часто встречаются в классических архитектур-
