2.1. Необходимые условия существования безусловного экстремума функции

Необходимые условия существования безусловного экстремума дифференцируемой функции даются в следующей теореме.

Теорема о необходимых условиях экстремума. Пусть дифференцируемая функция имеет в точке экстремум. Тогда все ее частные производные первого порядка в точке равны нулю:

. (2.2)

Условие (2.2) эквивалентно условию

. (2.3)

Следствие. Необходимым условием существования экстремума дифференцируемой функции в некоторой точке является условие стационарности этой точки. Градиент дифференцируемой функции в точке экстремума равен нулю.

Замечание 2.1. Если функция не является дифференцируемой, то необходимыми и достаточными условиями существования безусловного экстремума являются условия определения безусловного экстремума.

2.2. Достаточные условия существования безусловного экстремума функции

Достаточные условия существования экстремума дважды дифференцируемой функции даются в следующей теореме.

Теорема о достаточных условиях экстремума. Пусть функция имеет непрерывные производные второго порядка в стационарной точке . Тогда точка является точкой безусловного максимума, если матрица Гессе функции в этой точке отрицательно определена и точкой безусловного минимума, если матрица Гессе функции в этой точке положительно определена.

2.3. Классический метод поиска безусловного экстремума

Классический метод поиска безусловного экстремума функции является методом решения ЗНЛП простейшего класса – ЗНЛП без ограничений:

В основе метода лежат сформулированные выше теоремы о необходимых и достаточных условиях существования безусловного экстремума. Метод применим только для "достаточно гладких" (дважды непрерывно дифференцируемых функций). Метод состоит в выполнении следующих шагов.

Шаг 1. Решить уравнение (или систему уравнений ) и найти множество ее решений – стационарных точек (подозрительных на экстремум).

Шаг 2. Установить, пользуясь теоремой об условиях определенности матрицы (критерием Сильвестра), тип определенности матрицы Гессе в каждой стационарной точке функции , и на основе этого сделать вывод о существовании и типе экстремума.

Замечание 2.2. Решение системы уравнений на первом шаге представляет собой отдельную, во многих случаях достаточно сложную задачу. Производные целевой функции нередко оказываются нелинейными функциями, а решение системы нелинейных уравнений аналитическими методами возможно не всегда. Поэтому иногда для выявления стационарных точек на первом шаге приходится применять так называемые численные методы (см., например, метод Ньютона-Рафсона, описанный ниже).

Замечание 2.3. Если при реализации классического метода матрица Гессе в стационарной точке не является ни положительно, ни отрицательно определенной, то тогда необходимо более детальное исследование поведения функции в этой точке (например, разложение по формуле Тейлора и анализ этого разложения).

Пример 2.2. Прибыль P некоторой фирмы определяется как

,

где расходы на производство; и расходы на рекламу по радио и телевидению соответственно. Требуется в условиях отсутствия ограничений на производственные и рекламные затраты определить максимально возможную прибыль, а также значения аргументов обеспечивающие этот максимум.

Решение. Необходимо решить ЗНЛП без ограничений:

.

Целевая функция является дифференцируемой, поэтому в данном случае применим классический метод решения. Реализуя этот метод, имеем:

шаг 1. Из условия получаем систему линейных уравнений

По теореме Крамера система имеет единственное решение – единственную стационарную точку . Только в этой точке может быть экстремум.

шаг 2. Для определения типа экстремума вычисляем матрицу Гессе и устанавливаем ее определенность в стационарной точке. Имеем

.

Таким образом, матрица Гессе функции в стационарной точке есть

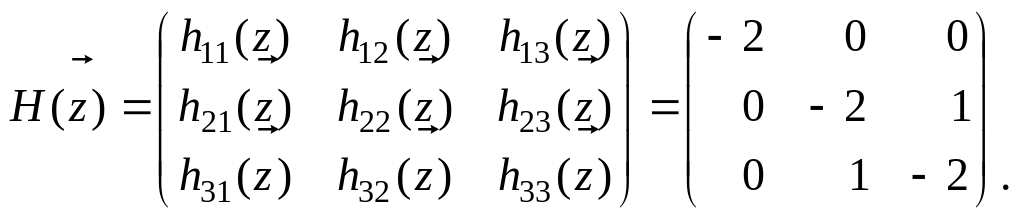
Установим тип определенности . Для главных ее миноров имеем

; ; .

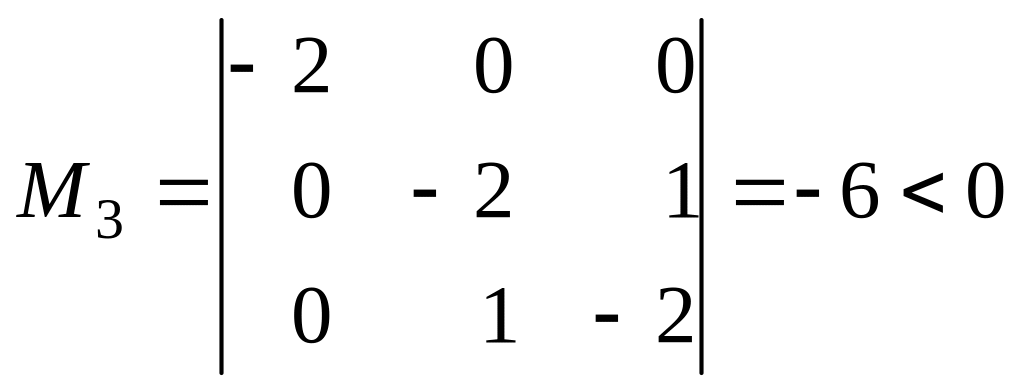По теореме об условиях определенности матрицы (критерию Сильвестра) найденная матрица Гессе является отрицательно определенной. Следовательно, стационарная точка есть точка максимума. Искомые значения обеспечивающие максимум прибыли, равны . Максимальная прибыль при этом оказывается равной

.