Тема 1. Векторная алгебра

Программы письменных теоретических опросов (на 10 минут)

Первый теоретический опрос.

Знать определения: направленного отрезка, нулевого направленного отрезка, длины направленного отрезка, коллинеарных направленных отрезков, сонаправленных и противоположно направленных направленных отрезков, вектора, длины вектора, коллинеарных векторов, сонаправленных и противоположно направленных векторов, противоположных векторов, вектора параллельного плоскости, компланарных векторов. Суммы векторов, разности векторов, произведения вектора на число.

Знать формулировки: свойства сложения векторов, свойства произведения вектора на число, теорему о разности векторов, теорему о коллинеарных векторах, теорему о компланарных векторах.

Второй теоретический опрос.

Знать определения: системы линейно зависимых и линейно независимых векторов, базиса векторного пространства, ортонормированного базиса, координат вектора в данном базисе, угла между векторами, скалярного произведения векторов.

Знать формулировки: свойства систем линейно зависимых и линейно независимых систем векторов, теоремы 1, 2, 3 о линейной зависимости систем из одного двух и трех векторов и следствия из них, теорема о координатах вектора, теорему о вычислении скалярного произведения в ортонормированном базисе и следствия из нее, свойства скалярного произведения векторов.

СУММА ВЕКТОРОВ И ПРОИЗВЕДЕНИЕ ВЕКТОРА НА ЧИСЛО

Вектором называется множество всех направленных отрезков пространства, любые два из которых сонаправлены и имеют равные длины, эти направленные отрезки будем называть представителями вектора а. Векторы будем обозначать жирными буквами, например, вектор а, Если направленный отрезок а, то вектор а можно обозначать АВ.

Длиной вектора называется длина любого его представителя.

Векторы а и b называются сонаправленными, если любые два их представителя сонаправленны, будем обозначать сонаправленные векторы так: а ↑↑ b. Векторы а и b называются противоположно направленными, если любые два их представителя противоположно направлены, будем обозначать противоположно направленные векторы так: а ↑↓ b.

Вектор называется параллельным прямой, если любой его представитель либо параллелен прямой, либо лежит на этой прямой. Два вектора а и b называются коллинеарными, если они параллельны одной прямой. Коллинеарные векторы будем обозначать так а││ b.

Вектор называется параллельным плоскости, если любой его представитель либо параллелен плоскости, либо лежит в этой плоскости. Три и более векторы называются компланарными, если они параллельны одной плоскости. (Любые два вектора компланарны)

Если дан вектор а и точка О, то существует единственная точка А, такая, что АВ = а, будем в этом случае говорить, что вектор а отложен от точке А. Договоримся под словами «построить вектор а» понимать отложить вектор а от какой либо точки О, т.е. построить точку А такую, что а = ОА.

Противоположными векторами называются такие два вектора, которые противоположно направлены и длины которых равны. Вектор, противоположный вектору а, обозначается так (- а).

Суммой векторов а и b называется вектор с, который получается следующим образом: от произвольной точки А отложим вектор АВ = а, от точка В отложим вектор ВС = b, тогда с = а + b = АС. Указанное в этом определении правило сложения векторов называется правилом треугольника. (Рис. 1) Если векторы а и b не коллинеарны, то можно от произвольной точки О отложит векторы ОА = а и ОВ = b, построить параллелограмм ОАСВ, тогда вектор ОС = а + b. Сложение векторов по этому правилу называется правилом параллелограмма (Рис. 2)

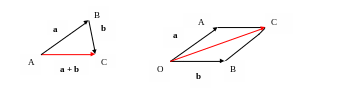
Рис. 1 Рис. 2

Сложение векторов обладает следующими свойствами:

1°. Для любого вектора а а + 0 = 0 + а.

2°. Для любого вектора а а + (- а) = (- а) + а = 0.

3°. Для любых векторов а и b a + b = b + a (свойство коммутативности).

4°. Для любых трех векторов a, b, c (a + b)+ c = a + (b + c) (свойство ассоциативности).

Произведением число λ на вектор а (или произведением вектора а на число λ ) будем называть вектор b = λ а, удовлетворяющей двум условиям: 1)длина вектора b равна произведению модуля числа λ и длины вектора а │ b│= │ λ ││а│, 2) если λ 0, то вектор b сонаправлен с вектором а, если λ < 0, то вектор b противоположно направлен с вектором а.

Произведение вектора на число обладает следующими свойствами:

1°. Для любого вектора а 1 а = а.

2°. Для любого вектора а 0 а = а.

3°. Для любого вектора а и любых чисел λ и β (λ β) а = λ (β а).

4°. Для любого вектора а и любых чисел λ и β (λ+ β) а = λ а + β а.

5°. Для любых векторов а и b любого числа λ λ(a + b) = λa + λb.

Для решения задач данного раздела целесообразно придерживаться следующих рекомендаций: а) если надо построить алгебраическую сумму векторов, то все векторы со знаками минус заменяем на противоположные векторы со знаками плюс, б) сумма п векторов не изменится, если поменять местами любые два вектора, в) для построения суммы п векторов строим эту сумму по правилу п-угольника, т.е. сначала выбираем направленный отрезок из первого вектора, затем от его конца откладываем направленный отрезок из второго вектора, затем от конца этого отрезка откладываем направленный отрезок из третьего вектора и так далее, тогда соединив начало первого направленного отрезка с концом последнего направленного отрезка, получим направленный отрезок из искомой суммы.

ЗАДАЧА № 1

Дан правильный шестиугольник АВСДEF с центром О. Построить вектор

АВ – EF +2ОF.

РЕШЕНИЕ

F

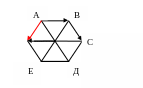
1. АВ – EF +2ОF = АВ + FE +2ОF

2. Рассмотрим направленный отрезок , от точки В отложим направленный отрезок из вектора FE, затем от точки С отложим направленный отрезок из вектора 2ОF.

Тогда АВ – EF +2ОF = АF.

ОТВЕТ. Искомая сумма равна вектору АF.

ЗАДАЧА № 2.

АВСДА₁В₁С₁Д₁ – параллелепипед. Построить вектор

- ½ С₁А₁ + СА₁ – ДА + ½ (СВ – В₁А₁)

РЕШЕНИЕ

1. – ½ С₁А₁ + СА₁ – ДА + ½ (СВ – В₁А₁) = ½ А₁С₁ + СА₁ + АД + ½ СВ + ½ А₁В₁

2. Поменяем местами слагаемые ½А₁С₁ + СА₁ + АД + ½ СВ + ½ А₁В₁ =

АД + ½ СВ + ½ А₁В₁ + ½ А₁С₁ + СА₁

3. Откладываем направленные отрезки из данных векторов следующим образом:

АД, ½ СВ, ½ А₁В₁, ½ А₁С₁, СА₁, где М – середина АД, О = АС ВД.

АД + ½ СВ + ½ А₁В₁ + ½ А₁С₁ + СА₁ = АА₁.

Замечание. Задачи такого типа имеет разные пути решения, но ответ должен быть один и тот же. При решении данной задачи можно было рассуждать следующим образом:

– ½ С₁А₁ + СА₁ – ДА + ½ (СВ – В₁А₁) = ½ А₁ С₁ + СА₁ + АД + ½ (СВ +

А₁ В₁) = ½ АС + СА₁ + АД + ½ (СВ + ДС) = ½ АС + СА₁ + АД + ½ ДВ =

ОС + СА₁ + АД + ДО = (ДО + ОС) + СА₁ + АД = ДС + СА₁ + АД =

ДА₁ + А₁Д₁ = ДД₁ = АА₁.

Существуют и другие пути построения искомого вектора.

ОТВЕТ. Искомая сумма равна вектору АА₁.

Решить следующие задачи.

1. Дан параллелограмм АВСД . Построить векторы: а) - 2/3 АВ, б) АД, в) АВ + АД, г) ¾ АВ + 1/3 АД –2/3 ДА – ¼ ВА, г) АД + ½ АВ – ВС – ½ СД.

2. Дан правильный шестиугольник АВСДEF с центром О. Построить векторы а) FА + ВС – ЕО, б) ½ ДЕ + ¾ ЕF – ½ В F + ½ ЕД.

3. Дан параллелепипед АВСДА1В1С1Д1. N, К, М – середины ребер Д1С1, ВС, СС1. Построить Векторы а) АА1 + ДС – ДА – ½ АВ, б) С1С + 1/3 АД + Д1С1 – 2/3 С1В1 – ½ Д1Д, в) СК + С1Д1 – NД + АД.

4. АМ – медиана треугольника АВС Доказать, что АМ = ½ (АВ + АС).

5. Дан тетраэдр АВСД. К – точка пересечения медиан грани ВСД. M, N, S – середины ребер СД, ВД, АС. Построить векторы

а) ВS + ½ АС – ½ КВ + 2/3 СN , б) 1/3 АС – 1/3 ВА – 2/3 СN + 1/3 АД.

6. Дан параллелепипед АВСДА₁В₁С₁Д₁. М и N – середины ребер Д₁С₁ и АД, , О = В₁С ВС₁. Построить векторы: а) ½ ВС + СС₁ – ½ С₁А₁,

б) А₁Д₁ + ½ АВ – ВС₁ - С₁М + ½ (ВВ₁ + ВС),

в) С₁О + ½ СД – Д₁А + 1/6 ВА – 2/3 В₁А₁ – ½ ВС.

7. Пусть а и в – произвольные векторы. Показать, что 1) |а + в| | а | +| в |, При каком условии в этом соотношении имеет место знак равенства,

2) |а - в| | а | +| в |. При каком условии в этом соотношении имеет место знак равенства, 3) Существуют ли векторы а и в, для которых

|а + в| < | а | и |а + в| < | в |, 4) Существуют ли векторы а и в, для которых

|а + в| > | а | и |а + в| > | в |.

а _

8. Доказать, что если вектор а 0, то вектор | а | единичной длины и сонаправлен с вектором а.

9. М – точка пересечения медиан треугольника АВС, Р – середина АВ. Доказать, что для любой точке О пространства 1) ОР = ½ (ОА + ОВ) , в частности СР = ½ (СА + СВ), 2) ОМ = 1/3 ( ОА + ОВ + ОС ).

10. О – точка пересечения медиан треугольника АВС. Доказать, что

ОА + ОВ + ОС = 0.

ЗАМЕЧАНИЕ. Из этого свойства следует, что точка О является центром тяжести треугольника АВС. Поэтому точку пересечения медиан треугольника называют центром тяжести этого треугольника.

11. Основанием пирамиды МАВСД является параллелограмм АВСД, диагонали которого пересекаются в точке О. Доказать, что

МА + МВ + МС + МД = 4МО.

12. В тетраэдре АВСД М, К, Р – середины ребер ВС, СД, ДВ. Доказать, что АВ + АД + АС = АМ + АК + АР.

13. В треугольной призме АВСА₁ В₁С₁ М и М₁ – точки пересечения медиан оснований АВС и А₁В₁С₁. Доказать, что АА₁ + ВВ₁ + СС₁ =

3 ММ₁.

14. АВСД параллелограмм, О – произвольная точка пространства. Доказать, что ОА + ОС = ОВ + ОД.

15. Доказать, что если для некоторого четырехугольника АВСД и некоторой точки О пространства выполняется векторное равенство ОА + ОС = ОВ + ОД, то АВСД – параллелограмм.

ЗАМЕЧАНИЕ.

1) Даны векторы с₁, с₂, . . .с_п и числа α₁ , α₂ , … α_п . Вектор

α₁ с₁ + α₂ с₂ + … + α_п с_п называется линейной комбинацией векторов

с₁ , с₂ , … с_п , а числа α₁ , α₂ , … α_п называются коэффициентами этой линейной комбинации.

Если вектор а является линейной комбинацией векторов с₁, с₂, . . .с_п, т.е.

а = α₁ с₁ + α₂ с₂ + … + α_п с_п, то будем говорить, что вектор а выражен через векторы с₁, с₂, …с_п или что вектор а разложен по векторам с₁, с₂, …с_п .

2) Если некоторый вектор надо выразить через данные векторы, то сначала вектор а мы представляем как сумму некоторых векторов или как произведение некоторого вектора на число. Затем с каждым полученным таким образом вектором поступаем аналогично, пока не получим линейную комбинацию данных векторов. Проиллюстрируем это, решая задачу 3.

ЗАДАЧА № 3

Дан тетраэдр АВСД. К – середина ребра ВС, точка М принадлежит ребру АД и ДМ = 1/3 ДА. ДМ = а, СА = в, АК = с. Выразить вектор ВД через векторы а, в, с.

РЕШЕНИЕ.

1. Представим вектор ВД как сумму двух векторов: ВД = ВС + СД. (1)

2. Теперь постараемся вектор ВС представить в виде линейной комбинации векторов а, в, с.

ВС = 2 КС = 2 ( КА + АС) = 2 ( -с + в) (2).

3. Теперь выразим вектор СД как линейную комбинацию векторов а, в, с.

СД = СА + АД = в + 3 МД = в – 3 а. (3)

4. В равенство (1) подставит разложения векторов ВС и СД из равенств (2) и (3). ВД = 2 ( -с + в) + в – 3 а = - 3 а + 3 в – 2 с.

ОТВЕТ . ВД = - 3 а + 3 в – 2 с.

16. Дан правильный шестиугольник АВСДEF с центром О.

а) Выразить векторы ВС, ВЕ, АЕ через векторы FА и FО.

б) Выразить векторы ВС, ВЕ, FД через векторы ВА и ВД.

17. АВСД – тетраэдр. М, N, Р, Q – середины ребер АД, АВ, ВС, СД.

а) Выразить векторы МN и РА через векторы АВ, ВД, ДС.

б) Выразить векторы АР и Q N через векторы АС, А N, АД.

18. АВСДА₁В₁С₁Д₁ – куб. О = В₁С ВС₁, М – середина АВ.

а) Выразить вектор АО через векторы АС, АД, ВД₁.

б) Выразить векторы СМ, Д₁О, СА₁ через векторы АС, АД, АА₁.

ЗАДАЧА № 4

Дан угол АОВ, выразить через векторы ОА и ОВ какой либо вектор, параллельный биссектрисе этого угла

Р

С

ЕШЕНИЕ

b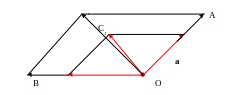

Построим параллелограмм ОАСВ. По правилу параллелограмма вектор ОС = ОА + ОВ. Если длины векторов ОА и ОВ не равны, то ОС не является биссектрисой угла АОВ. Если ж длины этих векторов равны, то ОАСВ – ромб, а т.к. диагонали ромба делят его углы пополам, то ОС будет

ОА ОВ

биссектрисой угла АОВ. По задаче 8 векторы | ОА | | ОВ| сонаправлены с векторами ОА и ОВ и каждый из них имеет длину единица, обозначим эти векторы а и b, сумма векторов а + b = ОС₁ будет параллельна биссектрисе угла АОВ.

ОТВЕТ. Вектор ОА + ОВ параллелен биссектрисе угла АОВ.

| ОА | | ОВ|