4.3.2. Неприводимые многочлены в конечном поле k.
В этом разделе мы научимся
определять для заданного многочлена
с коэффициентами из конечного поля
P={0, 1, 2, ... q - 1}, является ли этот многочлен
неприводимым в поле P. Неприводимые
многочлены используются для построения
линейных сдвиговых регистров с обратной
связью (см. раздел 3.1.6). Наш
алгоритм основывается на следующей
теореме.
Теорема.
Пусть F – конечное поле, состоящее из q
элементов. Тогда для любого натурального
многочлен
является произведением всех неприводимых
над полем F многочленов степени k.
Из этой теоремы сразу следует,
что для произвольного многочлена
является произведением всех линейных
сомножителей
,
является произведением всех квадратичных
сомножителей
и т.д. Поэтому, если
=1
для
,
то
является неприводимым многочленом.
Наибольший общий делитель двух многочленов
находят с помощью алгоритма Евклида,
используя соотношение
,
где
-
остаток от деления
на
.
Упомянутый тест на неприводимость можно
заменить более быстрым альтернативным
тестом: многочлен
над полем F=
является неприводимым тогда и только
тогда, когда
,
и
для всех простых делителей k степени
n.
Пример.
Показать неразложимость многочлена
над полем F2={0,1}.
В данном случае, n=3, q=2. Для
вычисления
поделим
столбиком
на
и найдем остаток:
.
Остаток равен x. Простым делителям числа
n=3 являются только k=1, поэтому остается
только проверить, что
.
Для этого делим первый многочлен на
второй и находим остаток
.
Теперь по алгоритму Евклида
.
Упражнение 1.
Являются ли неприводимыми над полем
F2={0,1}
трехчлены
,
,
,
,
?
Упражнение 2. Найдите все неприводимые многочлены третьей степени над полем F2.
Упражнение 3. Определите периоды линейных сдвиговых регистров с обратной связью, построенных на основе неприводимых трехчленов, найденных в предыдущих упражнениях.
Упражнение 4. Какой степени должен быть многочлен, чтобы длины порождаемой им им последовательности бит хватило для кодирования сообщения длины 1 гб?
Упражнение 5. Написать программу на каком-нибудь языке программирования, проверяющую является ли заданный многочлен неприводимым над конечным полем F.
4.4. Эллиптические кривые
Пусть GF(q),
представляет собой конечное поле с
характеристикой p. Эллиптическая кривая
определяется уравнением
Если характеристика p>3, то это уравнение эквивалентно следующему
(*)
Будем рассматривать в данном курсе только эллиптические кривые над полями характеристики p>3. Вид эллиптической кривой над полем действительных чисел показан ниже
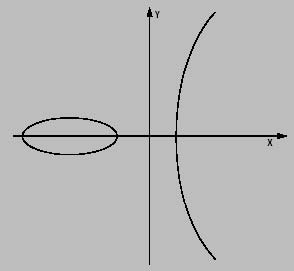
Рис.4.1. Эллиптическая кривая.
Математическое свойство, которое делает эллиптические кривые полезными для криптографии, состоит в том, что если взять две различных точки на кривой, то соединяющая их хорда пересечет кривую в третьей точке (так как мы имеем кубическую кривую). Зеркально отразив эту точку по оси Х, мы получим еще одну точку на кривой (так как кривая симметрична относительно оси X). Если мы обозначим две первоначальных точки как P и Q, то получим последнюю – отраженную – точку P+Q. Это «сложение» удовлетворяет всем известным алгебраическим правилам для целых чисел.
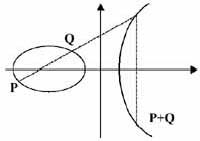
Рис.4.2. Геометрическая иллюстрация операции сложение точек на ЭК.
Эту операцию можно выразить
следующими формулами: суммой двух точек
и
является точка
с координатами, определяемыми следующими
соотношениями:
где
К точкам лежащим на ЭК добавляется еще одна специальная точка 0, которая называется бесконечно удаленной точкой.
Определим на точках ЭК операцию удвоения точки . Точкой 2P является по определению точка , удовлетворяющая уравнениям:
(**)
где
Из этих уравнений видно, что бесконечно удаленная точка 0 может быть получена, как результат удвоения точки Р с нулевой координатой y, либо при сложении двух различных точек с одинаковой координатой x.
Таким образом, мы можем определить конечную абелеву группу на точках кривой, где нулем будет являться бесконечно удаленная точка. В частности если точки P и Q совпадут, то можно вычислить P+P, т.е. 2P. Развивая эту идею, можно определить kP для любого целого числа k, и следовательно, определить значение P и значение наименьшего целого числа k, такого, что kP = F, где F – бесконечно удаленная точка. Теперь можно сформулировать «Проблему дискретного логарифма эллиптической кривой» (Elliptic Curve Discrete Logarithm Problem – ECDLP), на которой основана рассматриваемая система:
Даны базовая точка P и расположенная на эллиптической кривой точка Q=kP. Найти значение k.
Для эллиптических кривых и базовых точек решение таких уравнений представляет вычислительно сложную задачу. С точки же зрения криптографии мы имеем возможность определить новую криптографическую систему на основе эллиптических кривых.
Для каждой эллиптической кривой число точек в группе конечно, но достаточно велико. Оценка порядка (числа элементов) группы точек эллиптической кривой m такова:
,
где р — характеристика поля, над которым определена кривая. Если в схеме Эль-Гамаля рекомендуется использовать число р порядка 2512, то в случае эллиптической кривой достаточно взять p > 2255.
Упражнение.
Построить
абелеву группу точек кривой
.
В данном примере, а=0 и b=1. Если взять исходную точку P(0; 1), то по формулам (**)
,
откуда абсцисса т.2P
будет также равна нулю. Возьмем поэтому,
в качестве исходной точки, точку с
ненулевой координатой x,
например, P(2; 2). Имеем:
.
По формулам
(**)
,
,
.
Значит, т.2P=(2, 3). Найдем теперь т. 3P:
.
По формулам (*)
,
откуда 3P
= 0 – бесконечно удаленная точка.