4.3. Абелевы группы и конечные поля.

4.3.1. Основные определения и примеры.

Богатым источником алгоритмов и односторонних функций в криптографии служат различные алгебраические структуры. Мы определим здесь важные понятия группы, кольца и поля.

Определение 1. Группой называется непустое множество, на элементах которого определена двухместная операция, обозначаемая ◦ и называемая в зависимости от контекста сложением или умножением, причем выполняются три аксиомы:

1. Ассоциативность

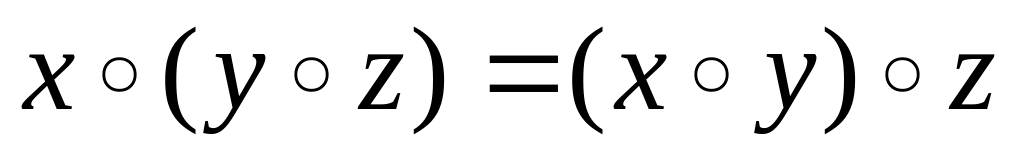
2. Существует некоторый элемент 1, называемый единицей группы, со следующим свойством .

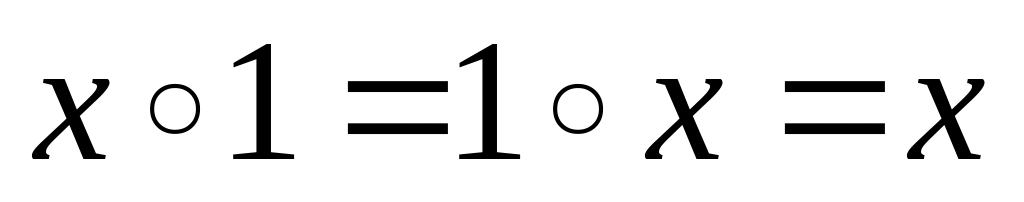3. Для каждого элемента x найдется элемент y, удовлетворяющий соотношению 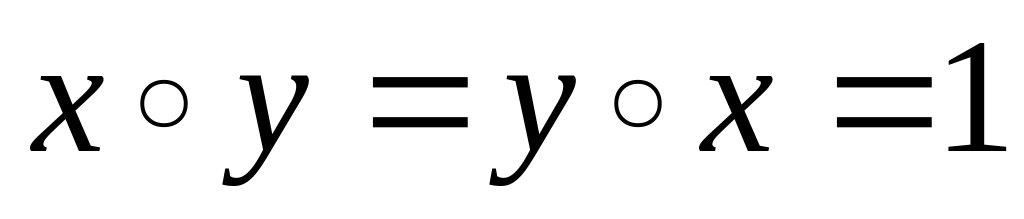. Этот элемент называется обратным к x и обозначается через .

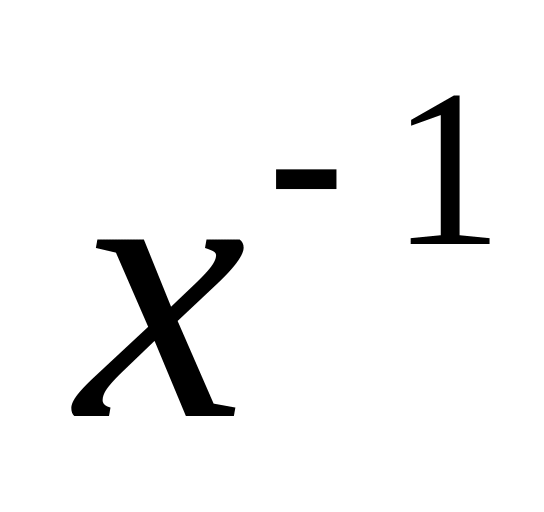Если дополнительно для любых элементов x и y выполняется свойство дистрибутивности , то группа называется абелевой.

Пример 1. Простым примером абелевой группы служит множество всех целых чисел Z вместе с операцией обычного сложения целых чисел, единицей 0 и операцией нахождения обратного элемента для x как (–x).

Пример 2. Группа классов вычетов Z_N по модулю числа N. Зафиксируем натуральное число N. На множестве целых чисел введем отношение эквивалентности, полагая два натуральных числа i и j эквивалентными по модулю N, если разность i – j делится нацело на N.

Множество классов эквивалентности, называемых классами вычетов или просто вычетов, образуют абелевую группу относительно операции сложения. Такая группа содержит ровно N элементов, обозначаемых через .

Степенью k элемента x называется элемент произведение элемента x на себя, взятое k раз. По определению . Группа называется циклической, если существует элемент x такой, что каждый элемент этой группы равен некоторой степени элемента x. При этом x называется порождающим элементом группы.

Пример 3. Более сложным примером группы является множество квадратных матриц размерности 2x2 с ненулевым определителем. В качестве групповой операции ◦ берется операция умножения матриц, а единицей служит единичная матрица. Операция умножения матриц не коммутативна, поэтому группа матриц не является абелевой.

Кольца и поля.

Если на непустом множестве G определены две операции (обозначаемые через + и ◦ ), причем относительно сложения G является абелевой группой, для операции умножения выполняется свойство ассоциативности , а также свойства дистрибутивности

,

то такая структура называется кольцом.

Если в кольце K есть единичный (нейтральный) элемент 1 по умножению, то такое кольцо называется кольцом с единицей. Если K выполняется свойство , то K называется целостным кольцом или областью целостности.

Пример 1. Кольцом с единицей являются множество целых чисел Z с обычными операциями сложения и умножения.

Пример 2. Кольцом является множество классов вычетов Z_N по модулю числа N. При этом если N является простым числом, то Z_N целостное кольцо, а если N - составное, например N=6, то Z_N уже не является целостным кольцом, т.к. .

Пример 3. Кольцом является множество многочленов (полиномов) от переменной x вида с коэффициентами из поля K. С многочленами можно выполнять те же операции, что и с целыми числами, т.е. складывать, вычитать, перемножать, делить с остатком, находить наибольший общий делитель Н.О.Д. с помощью алгоритма Евклида.

Определение. Полем называется кольцо с единицей, в котором каждый ненулевой элемент обладает обратным . Другими словами, кольцо с единицей является полем, если множество ненулевых элементов образует группу по умножению. Эту группу называют мультипликативной группой поля F и обозначают символом F*.

Пример 1. Полями являются множества рациональных чисел Q, действительных чисел R, комплексных чисел C относительно операций сложения и вычитания.

Пример 2. Кольцо вычетов Z_N по модулю числа N является полем, если N – простое число. Число N называется характеристикой поля.

Пусть K – поле, а f(x) – многочлен, неразложимый в K в произведение многочленов меньшей степени. Такой многочлен называется неприводимым над полем K. Свойство неприводимости существенно зависит от свойств поля K, поскольку если в качестве K взять поле комплексных чисел, то любой многочлен является разложимым в произведение линейных многочленов. Подобно кольцу классу вычетов Z_N можно рассматривать классы эквивалентности по модулю многочлена f(x).

Пример 3. Кольцо вычетов многочленов по модулю неприводимого многочлена f(x) с коэффициентами из поля K образует поле.

Если K – конечное поле, содержащее p элементов (p – простое число), а f(x) – многочлен степени m, то поле вычетов содержит элементов. Такие поля называются полями Галуа в честь выдающегося французского математика Эвариста Галуа, погибшего на дуэли в 20-летнем возрасте, и обозначают символом . В курсе алгебры доказывается, что любое конечное поле является полем Галуа для некоторого основания p и степени m. Еще один важный факт, касающийся полей Галуа, состоит в том, что мультипликативная группа конечного поля K всегда является циклической, т.е. существует порождающий элемент x такой, что любой ненулевой элемент y поля K является степенью x