51. Понятие двойного интеграла

Придел последовательности интегрируемых сумм

при n^(к)∞ (или ∆S^(к)0)-Двойной интеграл по плоской области D от функции f(M) и обозначается как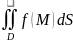

т.е.

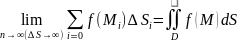
если придел интегрируемой суммы существует, то функция f(M) называется интегрируемой

Достаточное условие игнтегрируемости: Если функция f(M) ограничена и граница области D имеет конечное число угловых точек (точек излома), то двойной интеграл принемает конечное значение и функция f(M)-интегрируема по области D.

Замечание 1 Ограничение на f(M) 1) Мб не прирывной и иметь конечное число точек и линий излома 2) МБ разрывной и иметь конечное число точек и линий разрыва 1го порядка

Геометрический смысл дойного интеграла:

1)Если f(M)≥0, то гдеV_D-объем цилиндрического тела, нижнее основание котороого обл D, а верхнее основание = поверхность описываемая уравниением z=f(M), а боковая поверхность – цлиндрическая.

2)Если значение f(M) могут быть как положительные так и отрицательные, т.е

f(M) =

Замечание 2 (инвариантность 2го интеграла) Т.К при процедуре определения 2го интеграламы не пользовались системой координат Oxyz, то 2ой интеграл по обл D не зависти от системы координат, т.е.инвариантен относительно системы координат

Замечание 3 При вычислениии 2го интеграла в системе координат Oxyz удобно представлять в виде 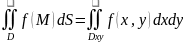, где f(M)=f(M(x,y))≡f(x,y)

52.Свойства двойного интеграла

1°. Аддитивность. Если функция f(x, y) интегрируема в области D и если область D при помощи кривой Г площади нуль разбивается на две связные и не имеющие общих внутренних точек области D₁ и D₂, то функция f(x, y) интегрируема в каждой из областей D₁ и D₂, причем

2°. Линейное свойство. Если функции f(x, y) и g(x, y) интегрируемы в области D, а α и β - любые вещественные числа, то функция [α · f(x, y) + β · g(x, y)] также интегрируема в области D, причем

3°. Если функции f(x, y) и g(x, y) интегрируемы в области D, то и произведение этих функций интегрируемо в D.

4°. Если функции f(x, y) и g(x, y) обе интегрируемы в области D и всюду в этой области f(x, y) ≤ g(x, y), то

5°. Если функция f(x, y) интегрируема в области D, то и функция |f(x, y)| интегрируема в области D, причем

(Конечно, из интегрируемости |f(x, y)| в D не вытекает интегрируемость f(x, y) в D.)

6°. Теорема о среднем значении. Если обе функции f(x, y) и g(x, y) интегрируемы в области D, функция g(x, y) неотрицательна (неположительна) всюду в этой области, M и m - точная верхняя и точная нижняя грани функции f(x, y) в области D, то найдется число μ, удовлетворяющее неравенству m ≤ μ ≤ M и такое, что справедлива формула

В частности, если функция f(x, y) непрерывна в D, а область D связна, то в этой области найдется такая точка (ξ, η), что μ = f(ξ, η), и формула (11) принимает вид

7°. Важное геометрическое свойство. равен площади области D (Это свойство, как уже отмечалось ранее, непосредственно вытекает из определения интегрируемости, данного в пункте