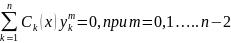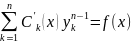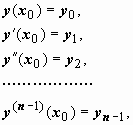26. Уравнение Бернулли. Его решение

y’=P(x)y+Q(x)y^m, если m=0, то уравнение с разделяющимися переменными, m=1, аналогично m>1 , то имеем место подстановка:

y(x)=U(x)*V(x)

Y’(x)=(UV)’=U’V+V’U=P(x)UV+Q(x)(UV)^m

V(U’-P(x)U)+UV’=Q(UV)^m

U’-P(x)U=o => =>

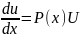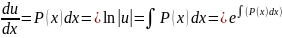
UV’=Q(UV)^m

+-

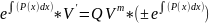
пример: Y’=y/x+x²/y

замена:y=UV

y’=U’V+UV’

U’V+UV’=UV/x+x²/UV

V(U’-U/x)+UV’=x²/UV

U’-U/x=0

or

UV’=x²/UV

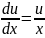
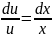
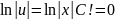
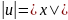
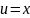
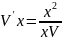
dV=dx/V

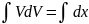
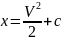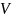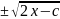=> = далее вывод у и у’

27. Решение линейного диф-го уравнения 1го порядка методом Лагранжа

yⁿ+a₁y^n-1++a₂y^n-2 ………+a_ny=f(x) дифф.уравнение

пусть y₀(x)=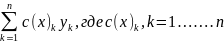

требуется выполнить опр. условия:

1. 

2. 

Тогда имеем:

//система открывается//

m=0: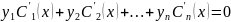

m=1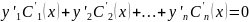

………………..

m=i:

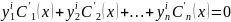
m=n-2:

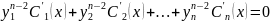
m=n-1: тупо степени n-1 и равно все f(x)

//система закрыта//

Матричный вид такой системы:

* =

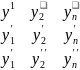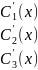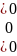
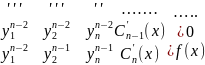
решается как обычные матрицы

=W(x)!=0-определитель

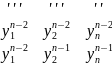
тогда общее решение: y(x)=y₀(x)+y^-(x)

28. Уравнение в полных дифферен. И его решение

=

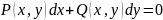
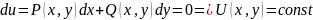
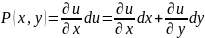
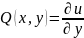
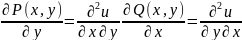
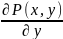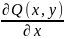
Пример

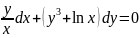
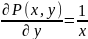
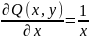
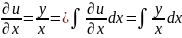
U(x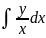,y)= +f(y)

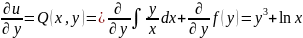
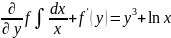
lnx+f’(y)=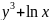

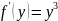
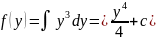
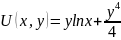+c

U(x,y)=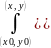

29. Постановка задачи Коши для уравнения n-го порядка: требуется найти решение уравнения

;

(17)

удовлетворяющее начальным условиям

(18)

где y₀, y₁, y₂, …, y_n-1 - заданные числа. В случае уравнения второго порядка это означает, что требуется найти решение, проходящее через заданную точку (x₀, y₀,) с заданным угловым коэффициентом y₁.

Уравнение вида решается последовательным n-кратным интегрированием. Пример: Переобозначивпостояные, общее решение запишем в виде y = cosx + C₁x³ + C₂x² + C₃x + C₄.

Общий и частный интегралы. Общее и частное решения

Рассмотрим некоторую функцию y=  (х,с), где с есть параметр или постоянная. Найдем дифференциальное уравнение, которому эта функция удовлетворяет. Возьмем производную от функции y, получим y' =  '(х,с). Если в этой операции будет исключено с, т.е. получается y' =  (x), то это и будет дифференциальным уравнением первого порядка, разрешенным относительно производной, а y =  (х,с) является его решением; очевидно, в этом случае зависимость y от с линейна, т.е. y =  (х)+c. Но допустим, что в  '(х,с) содержится с. Выражение y' =  '(х,с) нельзя назвать дифференциальным уравнением (ввиду неопределенности с) до тех пор, пока из выражения y' =  '(х,с) не исключим с. Для этого разрешим уравнение y =  (х,с) относительности: с =  (х,с). Это возможно, если функция  (х,с) имеет отличную от нуля производную (по теореме о существовании обратной функции), т.е. . Пусть это условие выполнено, тогда, подставив с =  (х,с) в выражение y' =  '(х,с), получим y' =  '(х,  (х,с)) - искомое дифференциальное уравнение, решением которого будет y =  (х,с). Итак, функция, зависящая от одной произвольной постоянной y =  (х,с), тогда является общим решением дифференциального уравнения, когда выполнено условие:  . Слово "общее" означает, что все частные функции, удовлетворяющие уравнению y' =  '(х,  (х,с)) могут быть получены из функции y =  (х,с) приданием с определенных значений.

Пусть дана неявная функция одной переменной  (х,y,с)=0, содержащая одну произвольную переменную. Найдем дифференциальное уравнение, для которого эта неявная функция будет решением. Для этого продифференцируем  (х,y,с)=0. Получим  . Разрешая  (х,y,с)=0 относительно с =  (x,y) и вставляя его в уравнение  , получим искомое дифференциальное уравнение

Решение дифференциального уравнения первого порядка, записанное в виде  (х,y,с)=0, зависящее от произвольной постоянной, является общим интегралом. Рассмотрим теперь неявную функцию от одной переменной и n произвольных постоянных (х,y,с₁,с₂, ... ,с_n)=0 (*)

Получим дифференциальное уравнение, для которого эта функция будет решением. Допустим, что  (х,y,с₁,с₂, ... ,с_n) имеет производные по переменным x, y,n-гопорядка. Дифференцируя   (х,y,с₁,с₂,...,с_n)=0n раз, получим

(**)

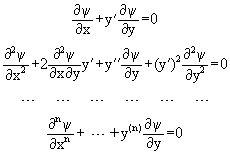Рассмотрим совместно выражения (*) и (**). Объявим в этих выражениях неизвестными с₁,с₂, ... ,с_n. Тогда (*) и (**) составляют систему n+1 уравнений, из которых можно исключить n произвольных постоянных. В результате получим уравнение n-го порядка F(х,y,y',y'', ... ,y⁽ⁿ⁾)=0. Выражение (*) является общим интегралом этого уравнения. Функция (*) называется общим интегралом уравнения тогда, когда после n-кратного дифференцирования образуется система конечных уравнений (*) и (**), допускающая существование единственного решения для постоянных с₁,с₂, ... ,с_n. Если (*) можно разрешить относительно y =  (х,с₁,с₂, ... ,с_n), то получим общее решение уравнения.

Частным интегралом или частным решением дифференциального уравнения называется общий интеграл или общее решение, для которых указаны конкретные значения произвольных постоянных. Для определения произвольных постоянных необходимо задать столько условий, сколько постоянных. Эти условия включают задание значения функции и ее производных в определенной точке. Так для уравнения n-го порядка необходимо задать Числа  называются начальными значениями, эти равенства - начальными условиями.