12. Понятие ортогональной системы действительной функций. Ортогональность основной тригонометрической системы

Определение1. Система (множество, совокупность) функций, определенных на отрезке  , называется ортогональной на этом отрезке, если        при          и

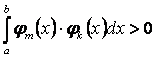  при   ,  то есть    .

Теорема 1. Интеграл от периодической функции по любому отрезку, длина которого равна положительному периоду, не зависит от выбора отрезка интегрирования.

Действительно, пусть Т > 0 - период функции f(x),  а – произвольное действительное число.  Докажем, что

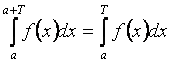  . По свойству аддитивности определенного интеграла

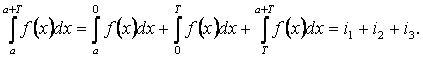
В интеграле i₃ сделаем замену переменной: пусть x=t+T,  тогда t=x-T, dx=dt,  t_в =a+T-T= a;  t _н = T-T = 0:

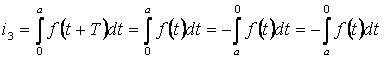
  (т.к. определенный интеграл не зависит от обозначения переменной интегрирования).

Получили: i₃=-i₁, следовательно  , что и требовалось доказать.

Теорема 2.  Тригонометрическая система функций ортогональна на любом отрезке длины 2π.

Учитывая утверждение теоремы 1, доказательство проведем для симметричного отрезка  .

Сначала докажем ортогональность функции φ₁(х)=1 ко всем остальным:

,так как при любом натуральном k функция   нечетная, а отрезок интегрирования симметричен.

.

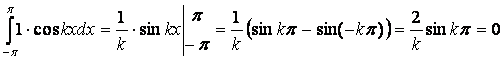Теперь докажем ортогональность всех синусов всем косинусам:

 при любых k и m   N (даже при любом k = m), т.к. подынтегральная функция нечетная.

Далее докажем ортогональность косинусов с разными аргументами, т.е. при k ≠ m: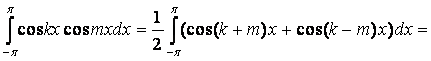 

,

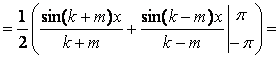
 т.к.   при любом р.

Теперь проверим ортогональность синусов с различными аргументами, т.е. при k≠m:   

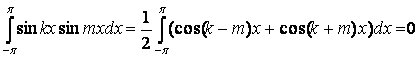
(см. предыдущий интеграл).

Осталось вычислить интегралы от квадратов функций системы:

Теорема доказана.

Определение 3. Функциональный ряд вида    ,                                (1)

составленный из функций тригонометрической системы с помощью действительных чисел,   где   называется тригонометрическим рядом, а числа    его коэффициентами. Очевидно, если ряд (1) сходится и точке х_о, то он сходится и в точках   где  , т.к. члены ряда есть 2π—периодические функции. По той же причине и сумма ряда (1), если она существует, является 2π—периодической функцией.

 Заметим, что поведение тригонометрического ряда (его сходимость или расходимость в каких-то точках) полностью определяется его коэффициентами.

Ортогональность основной тригонометрической системы

Система функций 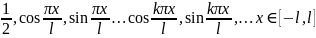, (1) называется основной тригонометрической системой. Эта система ортогональна на отрезке .

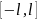Можно показать, подсчитав интегралы вида 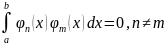и 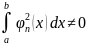, что система (1) является ортогональной системой на 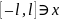и на любом отрезке оси OX, длиной 2l:

,

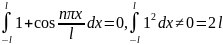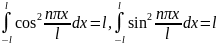. От системы (1) можно перейти к системе

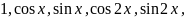
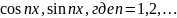путем замены переменной: .

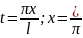13. Ортогональные системы действительных функций (определение, примеры). Разложение функции по ортогональным системам

Определение

Система функций  1,  cosx,  sinx,  cos2x,  sin2x,…,cosnx,  sinnx   называется тригонометрической.

Заметим, что все функции, входящие в систему:

φ₁(х)=1,  φ₂(х)=cosx,  φ₃(х)=sinx,  φ₄(х)=cos2x,  φ₅(х)=sin2x,…

являются периодическими с общим наименьшим положительным периодом  2π.

В самом деле, φ₁(х)=1—периодическая с любым, отличным от нуля периодом,  функции φ₂(х)=cosx и φ₃(х)=sinx имеют наименьший положительный период 2π, а функции cosпx  и sinпx имеют наименьший положительный период  . Поэтому число Т = 2π  является с одной стороны общим, а с другой стороны наименьшим  положительным периодом для всех функций, входящих в систему.

Рассмотрим несколько примеров тригонометрических рядов:

1)  .

Здесь   . Этот ряд расходится на всей числовой прямой, т.к. не выполняется необходимый признак сходимости: при   п-ый член   , а при     не существует.

2)  

Здесь  . Этот ряд сходится в точках   (т.к. в них  ) и расходится во всех остальных точках (в них   не существует).

3)   .

Здесь   . Этот ряд сходится на всей числовой прямой, причем абсолютно по признаку сравнения рядов с произвольными членами, т.к.   .

Разложение функции по ортогональным системам

Ортогональная система функций- задача о разложении функции f (x) в ряд вида  , где {jп (х)} -Ортогональная система функций Если положить формально  , где {jп (х)} - нормированная Ортогональная система функций, и допустить возможность почленного интегрирования, то, умножая этот ряд на jп (х) r(х) и интегрируя от а до b, получим:  (*) Коэффициенты Сп , называемые коэффициентами Фурье функции относительно системы {jn (x)}, обладают следующим экстремальным свойством: линейная форма   наилучшим образом приближает в среднем эту функцию. Иными словами, средняя квадратичная ошибка с весом r(х):     (*) имеет наименьшее значение по сравнению с ошибками, даваемыми при том же n другими линейными выражениями вида  . Отсюда, в частности, получается т. н. неравенство Бесселя

Ряд   с коэффициентами Сп , вычисленными по формуле (*), называется рядом Фурье функции f (x) по нормированнойОртогональная система функций {jn (x)}. Для приложений первостепенную важность имеет вопрос, определяется ли однозначно функция f (x) своими коэффициентами Фурье. Ортогональная система функций, для которых это имеет место, называется полными, или замкнутыми. Условия замкнутости Ортогональная система функций могут быть даны в нескольких эквивалентных формах. 1) Любая непрерывная функция f (x) может быть с любой степенью точности приближена в среднем линейными комбинациями функций jk (x), то есть   в этом случае говорят, что ряд   сходится в среднем к функции f (x)]. 2) Для всякой функции f (x), квадрат которой интегрируем относительно веса r(х), выполняется условие замкнутости Ляпунова - Стеклова: 3) Не существует отличной от нуля функции с интегрируемым на отрезке [a, b ] квадратом, ортогональной ко всем функциям jn (x), n = 1, 2,....