
- •2. Сравнение числовых рядов
- •12. Понятие ортогональной системы действительной функций. Ортогональность основной тригонометрической системы
- •13. Ортогональные системы действительных функций (определение, примеры). Разложение функции по ортогональным системам
- •14. Ряд Фурье. Представление периодической функции в виде ряда Фурье. Сходимость ряда Фурье (теорема Дирихле)
- •15. Разложение в ряд Фурье четных и не четных функций периодических функций. Разложение функций в ряд Фурье, заданной на полупериоде.
- •19. Интеграл Фурье в комплексной форме.
- •20. Теорема о существовании преобразования Фурье
- •21. Синус и косинус преобразования Фурье
- •26. Уравнение Бернулли. Его решение
- •27. Решение линейного диф-го уравнения 1го порядка методом Лагранжа
- •28. Уравнение в полных дифферен. И его решение
- •30. Линейные однородные ур-я 2-го порядка с постоянными коэ-ми. Их решение
- •31. Линейные неоднородные ур-я 2-го порядка с постоянными коэф-ми и правой частью спец. Вида
- •32. Линейные однород. Ур-ния n-го порядка
- •33. Решение линейных дифферен. Ур-ний n-го порядка с постоян коэф.
- •43. Непрерывность функции нескольких переменных
- •44. Частное приращение и частная производная функции нескольких переменных
- •45. Полное приращение функции нескольких переменных
- •47. Касательная плоскость
- •48. Частные производные высших порядков
- •51. Понятие двойного интеграла
- •52.Свойства двойного интеграла
- •53 Теоремы об оценке 2го интеграла
- •54 Техника вычисления 2го интеграла
- •55.Замена переменных в 2ом интеграле
1.Числовой
ряд. Пусть мы имеем числовую
последовательность
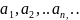 , где .
, где .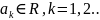 Числовой
ряд – это сумма членов числовой
последовательности вида
Числовой
ряд – это сумма членов числовой
последовательности вида
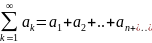
В
качестве примера числового ряда можно
привести сумму бесконечно убывающей
геометрической прогрессии со знаменателем
q = -0.5:
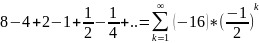
![]() называют
общим членом числового ряда или
k–ым членом ряда.
называют
общим членом числового ряда или
k–ым членом ряда.
Знакопеременные ряды Числовой ряд, содержащий бесконечное множество положительных и бесконечное множество отрицательных членов, называется знакопеременным.
Знакочередующиеся
ряды Частным случаем знакопеременного
ряда является знакочередующийся ряд,
то есть такой ряд, в котором последовательные
члены имеют противоположные знаки.
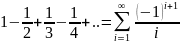
Знакопостоянные ряды Если все члены числового ряда имеют один и тот же знак, ряд называют знакопостоянным.
Конечная
(частичная) сумма ряда это сумма вида
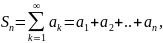 где n – некоторое натур. число.
где n – некоторое натур. число.
Понятие
сходимости ряда Числовой ряд
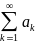 называется
сходящимся, если существует конечный
предел последовательности частичных
сумм
называется
сходящимся, если существует конечный
предел последовательности частичных
сумм
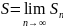 .
Если предел последовательности частичных
сумм числового ряда не существует или
бесконечен, то ряд называется расходящимся.
.
Если предел последовательности частичных
сумм числового ряда не существует или
бесконечен, то ряд называется расходящимся.
Сумма
ряда
называется предел последовательности
его частичных сумм, то есть,
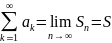
Абсолютная
сходимость ряда Знакопеременный ряд
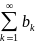 называется абсолютно сходящимся,
если сходится ряд из абсолютных величин
его членов, то есть, сходится
знакоположительный числовой ряд
называется абсолютно сходящимся,
если сходится ряд из абсолютных величин
его членов, то есть, сходится
знакоположительный числовой ряд
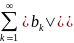
Условная сходимость ряда Знакопеременный ряд называется условно сходящимся, если ряд расходится, а ряд сходится.
2. Сравнение числовых рядов
Первый
признак сравнения рядов. Пусть
и
-
два знакоположительных числовых ряда
и выполняется неравенство
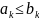 для всех k = 1, 2, 3, ... Тогда из сходимости
ряда
следует
сходимость
,
а из расходимости ряда
для всех k = 1, 2, 3, ... Тогда из сходимости
ряда
следует
сходимость
,
а из расходимости ряда
 следует расходимость
.
следует расходимость
.
Ряды-эталоны
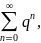 (геометр.ряд
сходится q<0);
(геометр.ряд
сходится q<0);
 ;
;
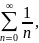 (ряд расходится);
(ряд расходится);
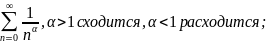
Пример:
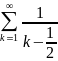 необходимое условие сходимости
выполняется
необходимое условие сходимости
выполняется
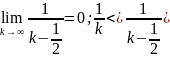 гармонический ряд
гармонический ряд

расходится, следовательно, по первому признаку сравнения исходный ряд также является расходящимся.
Второй
признак сравнения. Пусть
и
-
знакоположительные числовые ряды. Если
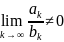 ,
то из сходимости ряда
,
следует сходимость
.
Если
,
то из расходимости числового ряда
,
следует расходимость
.
Следствие. Если
,
то из сходимости ряда
,
следует сходимость
.
Если
,
то из расходимости числового ряда
,
следует расходимость
.
Следствие. Если
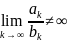 и
,
то из сходимости одного ряда следует
сходимость другого, а из расходимости
следует расходимость.
и
,
то из сходимости одного ряда следует
сходимость другого, а из расходимости
следует расходимость.
Пример: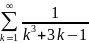 .
В качестве ряда
возьмем сходящийся ряд
.
В качестве ряда
возьмем сходящийся ряд
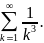 Найдем
предел отношения k-ых членов числовых
рядов:
Найдем
предел отношения k-ых членов числовых
рядов:
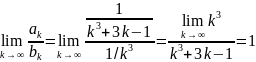 по второму признаку сравнения из
сходимости числового ряда
следует
сходимость исходного ряда.
по второму признаку сравнения из
сходимости числового ряда
следует
сходимость исходного ряда.
Третий
признак сравнения. Пусть
и
-
знакоположительные числовые ряды. Если
с некоторого номера N выполняется
условие
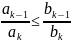 , то из сходимости ряда
следует сходимость
,
а из расходимости ряда
следует
расходимость
.
, то из сходимости ряда
следует сходимость
,
а из расходимости ряда
следует
расходимость
.
3.
Предельные признаки сходимости
и расходимости числовых рядов Если
числовой ряд
сходится, то предел его k-ого члена
равен нулю:
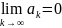 .
При
исследовании любого числового ряда на
сходимость в первую очередь следует
проверять выполнение необходимого
условия сходимости. Невыполнение
условия указывает на расходимость
числового ряда, то есть, если
.
При
исследовании любого числового ряда на
сходимость в первую очередь следует
проверять выполнение необходимого
условия сходимости. Невыполнение
условия указывает на расходимость
числового ряда, то есть, если
 .,
то ряд расходится. С другой стороны
нужно понимать, что это условие не
является достаточным. То есть, выполнение
равенства
.
не говорит о сходимости числового ряда
.
К примеру, для гармонического ряда
.,
то ряд расходится. С другой стороны
нужно понимать, что это условие не
является достаточным. То есть, выполнение
равенства
.
не говорит о сходимости числового ряда
.
К примеру, для гармонического ряда
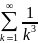 необходимое условие сходимости
выполняется
необходимое условие сходимости
выполняется
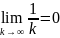 .,
а ряд расходится.
.,
а ряд расходится.
4. Знакопостоянные ряды Если все члены числового ряда имеют один и тот же знак, ряд называют знакопостоянным.
Радикальный
признак сходимости Коши
.
- знакоположительный числовой ряд. Если
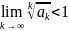 ,
то числовой ряд сходится, если
,
то числовой ряд сходится, если
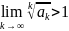 ,
то ряд расходится. Замечание. Признак
Коши справедлив, если
,
то ряд расходится. Замечание. Признак
Коши справедлив, если
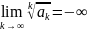 ,
то ряд сходится, если
,
то ряд сходится, если
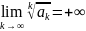 ,
то ряд расходится. Если
,
то ряд расходится. Если
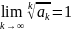 ,то
признак Коши не дает инфо о сходимости
или расходимости ряда и требуется доп.
исследование.
,то
признак Коши не дает инфо о сходимости
или расходимости ряда и требуется доп.
исследование.
Признак
сходимости Даламбера Пусть
-
знакоположительный числовой ряд. Если
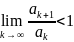 ,
то числовой ряд сходится, если
,
то числовой ряд сходится, если
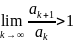 ,
то ряд расходится. Замечание. Если
предел бесконечен, то есть, если
,
то ряд расходится. Замечание. Если
предел бесконечен, то есть, если
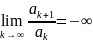 ,
то ряд сходится, если
,
то ряд сходится, если
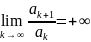 ,
то ряд расходится. Если
,
то ряд расходится. Если
 ,
то признак Даламбера не дает инфо о
сходимости или расходимости ряда и
требуется доп. исследование
,
то признак Даламбера не дает инфо о
сходимости или расходимости ряда и
требуется доп. исследование
5.
Интегральный признак сходимости Коши
числового рядам. Пусть
-
знакоположительный числовой ряд.
Составим функцию непрерывного аргумента
y = f(x), аналогичную функции
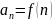 .
Пусть функция y = f(x) положительная,
непрерывная и убывающая на интервале
[a;+
.
Пусть функция y = f(x) положительная,
непрерывная и убывающая на интервале
[a;+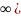 ,
где a
,
где a Тогда
в случае сходимости несобственного
интеграла
Тогда
в случае сходимости несобственного
интеграла
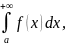 сходится
исследуемый числовой ряд. Если же
несобственный интеграл расходится, то
исходный ряд тоже расходится.
Пример.
Исследуйте числовой ряд с положительными
членами
сходится
исследуемый числовой ряд. Если же
несобственный интеграл расходится, то
исходный ряд тоже расходится.
Пример.
Исследуйте числовой ряд с положительными
членами
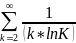 на сходимость.
Решение.
Необходимое
условие сходимости ряда выполнено, так
как
на сходимость.
Решение.
Необходимое
условие сходимости ряда выполнено, так
как
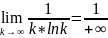 =0.
Рассмотрим функцию
=0.
Рассмотрим функцию
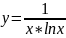 .
Она положительная, непрерывная и
убывающая на интервале
.
Она положительная, непрерывная и
убывающая на интервале
 . Функция непрерывна. Рассмотрим ф-юю
на убывание. Найдем производную:
. Функция непрерывна. Рассмотрим ф-юю
на убывание. Найдем производную:
 .
Она отрицательная на промежутке
,
следовательно, функция убывает на этом
интервале. Таким образом, функция
удовлетворяет условиям интегрального
признака Коши.
.
Она отрицательная на промежутке
,
следовательно, функция убывает на этом
интервале. Таким образом, функция
удовлетворяет условиям интегрального
признака Коши.
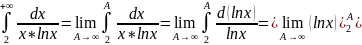 =
=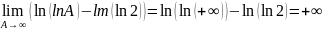 То
есть, несобственный интеграл расходится,
следовательно, расходящимся является
исходный числовой ряд.
То
есть, несобственный интеграл расходится,
следовательно, расходящимся является
исходный числовой ряд.
6. Знакочередующиеся числовые ряды Частным случаем знакопеременного ряда является знакочередующийся ряд, то есть такой ряд, в котором последовательные члены имеют противоположные знаки.
Абсолютная
и условная сходимость знакочередующего
ряда. Проще всего исследовать
знакопеременный числовой ряд
на
абсолютную сходимость. В этом случае
берем знакоположительный ряд
,
составленный из абсолютных величин
членов исходного ряда, и применяем к
нему подходящий достаточный признак
сходимости из рассмотренных выше. Если
ряд
,
сходится, то исходный ряд является
абсолютно сходящимся.
Пример.
Докажите, что знакопеременный числовой
ряд
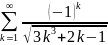 абсолютно
сходится/
Решение. Соответствующих
знакоположительный ряд будет иметь вид
абсолютно
сходится/
Решение. Соответствующих
знакоположительный ряд будет иметь вид
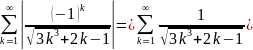 .
Для него выполняется необходимое условие
сходимости ряда, так как .
.
Для него выполняется необходимое условие
сходимости ряда, так как .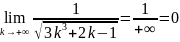 .
Возьмем сходящийся знакоположительный
ряд
.
Возьмем сходящийся знакоположительный
ряд
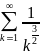 и воспользуемся вторым признаком
сравнения:
и воспользуемся вторым признаком
сравнения:
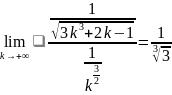 .
Следовательно, ряд
.
Следовательно, ряд
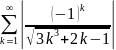 сходящийся, поэтому, исходный ряд
сходится абсолютно.
сходящийся, поэтому, исходный ряд
сходится абсолютно.
Если ряд , расходится, то соответствующий знакопеременный ряд , может, либо расходится, либо сходится условно. Только признак Даламбера и радикальный признак Коши позволяют сделать вывод о расходимости знакопеременного ряда , по расходимости ряда из модулей . Ряд также расходится, если не
выполняется
необходимое условие сходимости, то
есть, если
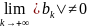 .
.
Признак
условной сходимости знакочередующего
ряда (признак Лейбница) Если абсолютные
величины членов знакочередующегося
ряда монотонно убывают
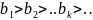 и
предел модуля общего члена ряда равен
нулю при
и
предел модуля общего члена ряда равен
нулю при
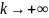 ,
то ряд
,
сходится.
Пример. Определите
характер сходимости знакочередующегося
числового ряда
,
то ряд
,
сходится.
Пример. Определите
характер сходимости знакочередующегося
числового ряда
 Решение.
Ряд
из абсолютных величин членов имеет вид
Решение.
Ряд
из абсолютных величин членов имеет вид
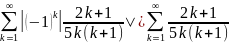 .
Для него выполняется необходимое условие
сходимости
.
Для него выполняется необходимое условие
сходимости
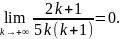 Возьмем гармонический ряд
и воспользуемся вторым признаком
сравнения:
Возьмем гармонический ряд
и воспользуемся вторым признаком
сравнения:
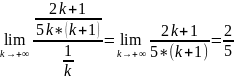 Таким образом, ряд из модулей
- расходящийся. В свою очередь,
знакочередующийся ряд
Таким образом, ряд из модулей
- расходящийся. В свою очередь,
знакочередующийся ряд
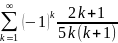 сходится, так как выполняются условия
признака Лейбница: последовательность
сходится, так как выполняются условия
признака Лейбница: последовательность
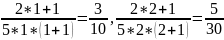 монотонно убывает и
Следовательно, исходный ряд условно
сходящийся.
монотонно убывает и
Следовательно, исходный ряд условно
сходящийся.
7.
Степенной ряд Ряд, членами которого
являются степенные функции аргумента
x, называется степенным рядом:
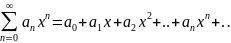
Часто
рассматривается также ряд, расположенный
по степеням (x − x0), то есть ряд
вида
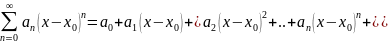 …,
где x0 − действительное число.
…,
где x0 − действительное число.
Интервал,
радиус сходимости и область сходимости
степенного ряда Рассмотрим функцию
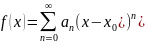 .
Ее областью определения является
множество тех значений x, при которых
ряд сходится. Область определения такой
функции называется интервалом
сходимости. Если интервал сходимости
представляется в виде
.
Ее областью определения является
множество тех значений x, при которых
ряд сходится. Область определения такой
функции называется интервалом
сходимости. Если интервал сходимости
представляется в виде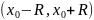 ,
где R > 0, то величина R называется
радиусом сходимости.
,
где R > 0, то величина R называется
радиусом сходимости.
Признак абсолютной сходимости Коши и Даламбера их связь с радиусом сходимости Радиус сходимости можно вычислить, воспользовавшись радикальным признаком Коши, по формуле
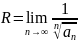 или
на основе признака Даламбера:
или
на основе признака Даламбера:
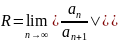
Схема нахождения области сходимости ряда
1)В
окрестности
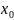 :
если
:
если
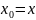 ,
то сумма =0, т.е ряд сходится.
,
то сумма =0, т.е ряд сходится.
2)
- Должен, выполнятся необходимый признак
сходимости
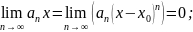
- Должен выполнятся признак Даламбера:
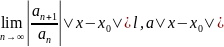 вынесем
из под предела т.к там нет n.
вынесем
из под предела т.к там нет n.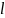 <1 сходится ,
<1 сходится ,
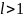 расходится,
=0, признак не работает.
расходится,
=0, признак не работает.
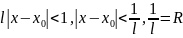 радиус сходимости
радиус сходимости
и
признак Коши
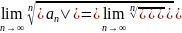 .
Пусть
.
Пусть
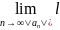 ,
,
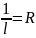 тогда возможны случаи
тогда возможны случаи
1.Если
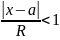 или
или
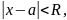 или
или
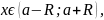 ,
то ряд сходится абсолютно.
,
то ряд сходится абсолютно.
2.Если
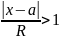 ,
то ряд расходится.
,
то ряд расходится.
Замечание.
Всякий степенной ряд сходится при x=a.
Если других точек сходимости у ряда
нет, то считают, что R=0.
Если степенной ряд сходится во всех
точках числовой прямой, то считают,
что![]() .
.
8.
Функциональный ряд
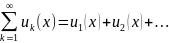 , т.е ряд, члены которого
, т.е ряд, члены которого
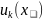 -некоторые
функции от x.При каждом
фиксированном значении х=
-некоторые
функции от x.При каждом
фиксированном значении х= функциональный ряд становится числовым
функциональный ряд становится числовым
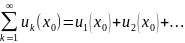
Область сходимости. Если ряд сходится, то значение аргумента х= называется точкой сходимости ряда. Множество всех точек сходимости х функционального ряда называется его областью сходимости
Сумма
функционального ряда
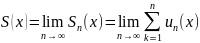 ,
,
Понятие
равномерной сходимости ряда Функциональный
ряд называется равномерно сходящимся
в некотором промежутке, если, каково бы
не было
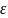 >0,
существует такое N, не
зависящее от х, что при n>Nдля
всех х из данного промежутка выполняется
неравенство
>0,
существует такое N, не
зависящее от х, что при n>Nдля
всех х из данного промежутка выполняется
неравенство
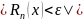 ,
где
,
где
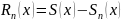
- остаток ряда.
