21. Синус и косинус преобразования Фурье

Если – четная, тогда

1)

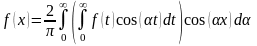
– косинус преобразования Фурье для .

Отсюда получаем

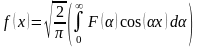
2)Если – нечетная, тогда

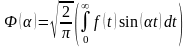– синус преобразования Фурье для .

Отсюда получаем .

22.

23. Понятие дифференциального уравнения. Общее и частное решение. Дифференциальным уравнением называется уравнение, связывающее независимые переменные, их функции и производные (или дифференциалы) этой функции.

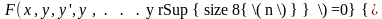
Порядок наивысшей производной входящей в уравнение определяет порядок дифференциального уравнения.

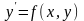- дифференциальное уравнение 1 порядка. (ДУI)

Функция 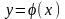называется решением, если при её подстановке в уравнение оно превращается в верное тождество. Решить уравнение – значит найти все его решения.

Функция 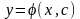называется общим решением, если при любом допустимом значении С эта функция является решением и любое другое решение получается из этого решения путем определенного выбора постоянного С. Если в общем решении выбрана конкретная постоянная С, то решение называется частным. Решение общее это некоторое семейство кривых.

Задача Коши. 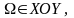в этой плоскости проходит через точку определенную прямая. Сколько проходит прямых? 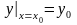Она одна и это доказывается теоремой об единственности, решение удовлетворяющее Коши является частным решением.

ДУI с разделяющимися переменными. Дифференциальное уравнение вида 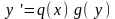называется ДУI с разделяющимися переменными.

Решение ДУI с разделяющимися переменными решают по схеме:

– обе части уравнения умножают на 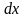, при этом уравнение принимает вид ;

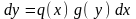– обе части уравнения делят на функцию 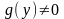, т.е. приводят уравнение к виду 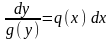(точки, в которых 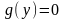определяют особые точки, при этом получаемые решения являются особыми);

Дифференциальное уравнение вида 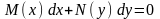называется

24. Линейные однородные уравнения первого порядка. Дифференциальное уравнение вида называется однородным, если его правая часть f(x, y) есть однородная функция нулевого измерения относительно своих аргументов. Любое уравнение вида 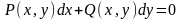является однородным, если функции P(x, y) и Q(x, y) – однородные функции одинакового измерения. Решение любого однородного уравнения основано на приведении этого уравнения к уравнению с разделяющимися переменными. Рассмотрим однородное уравнение 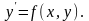Т.к. функция f(x, y) – однородная нулевого измерения, то можно записать: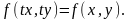 Т.к. параметр t произвольный, предположим, что 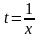. Получаем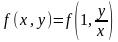 Правая часть полученного равенства зависит фактически только от одного аргумента 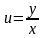, т.е. 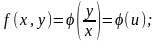Исходное дифференциальное уравнение таким образом можно записать в виде: Далее заменяем y = ux, 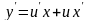. 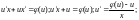таким образом, получили уравнение с разделяющимися переменными относительно неизвестной функции u.

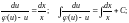Далее, заменив вспомогательную функцию u на ее выражение через х и у и найдя интегралы, получим общее решение однородного дифференциального уравнения.

25. Линейные Дифференциальное уравнение первого порядка вида 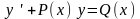называется линейным ДУ I.

Решение линейного ДУ I проводят по схеме:

1)– искомую функцию представляют в виде произведения двух функций, одну из которых можно выбрать произвольным образом, т.е. ;

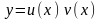– находят ее производную ;

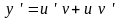– найденные величины подставляют в линейное ДУ I ;

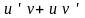
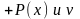
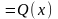– группируют, например, второе и третье слагаемые уравнения ;

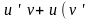
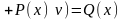– так как одну из функци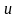й или 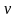можно выбрать произвольным образом, то выберем функцию так, чтобы выражение, записанное в круглых скобках обратилось в нуль, тогда уравнение будет эквивалентно системе дифференциальных уравнений первого порядка с разделяющимися переменными, т.е. ;

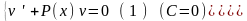– решают первое уравнение системы (при этом постоянную интегрирования выбирают равной нулю в силу произвольности отыскиваемой функции);

– найденную функцию подставляют во второе уравнение системы и решают его (при этом постоянная интегрирования будет произвольной и не равной нулю);

– находят искомую функцию .

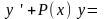
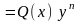
2) Дифференциальное уравнение первого порядка вида 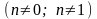называется уравнением Бернулли.

При 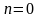уравнение Бернулли переходит в линейное ДУ I, а при 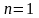– в ДУ I с разделяющимися переменными.

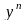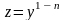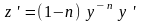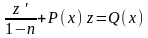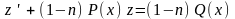Разделим все уравнение на , получим . Введем в рассмотрение новую функцию , тогда . Откуда находим, что величина . Подставим найденные величины в уравнение Бернулли , которое приводится к виду линейного дифференциального уравнения первого порядка . Следовательно, уравнение Бернулли можно решать непосредственно по схеме решения линейного ДУ I.