9. Неоднородные линейные дифференциальные уравнения второго порядка.

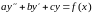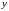Рассмотрим неоднородное линейное уравнение второго порядка с постоянными коэффициентами: . (12)Теорема 4. Обшее решение неоднородного уравнения (12) представляется как сумма

у=у_ч+У,

где у_ч - какое-нибудь частное решение уравнения (12), а У есть общее решение соответствующего однородного уравнения

ay + by + cy = 0 (13)

Следствие. Если 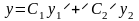- есть общее решение однородного уравнения (13), то общее решение уравнения (12) имеет вид:

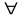y = y_ч + C₁ y₁ + C₂ y₂ C₁ ,C₂ ,

где y_ч - частное решение неоднородного уравнения (12).Таким образом, основная задача при решении уравнения (12) состоит в нахождении одного частного решения.

Общий метод нахождения частного решения называется

МЕТОДОМ ВАРИАЦИИ ПОСТОЯННЫХ

и состоит в следующем.Пусть есть ФСР уравнения (13). Частное решение уравнения (12) ищется в виде:

у_ч = С₁(x) y₁ + C₂(x)y₂ , (14)где C₁(x), C₂(x) есть неизвестные функции.Теорема 5. Функция (14) является частным решением уравнения (12),если функции C₁ = C₁(x), C₂ =C₂(x) удовлетворяют системе уравнений:

C₁ y₁ + C₂y₂ = 0 (15)

C₁ y₁ + C₂ y₂ = f(x) . (16)

Выразив из (15),(16) производные C₁, C₂ и проинтегрировав их, из (14) получим частное решение уравнения (12)4. Метод неопределенных коэффициентов. Метод вариации постоянных позволяет найти частное решение любого уравнения вида (12), однако, этот метод часто приводит к вычислению сложных интегралов.Для неоднородного уравнения (12) в случаях, когда правая часть представляется функциями специального вида, удается проще найти частное решение методом неопределенных коэффициентов.Рассмотрим здесь три таких случая:

1. Пусть f(x) = P_n(x), где P_n(x) многочлен n-ой степени.а) Если 0 не является корнем характеристического уравнения, то частное решение можно найти в таком же виде

y _ч = Q_n(x),где 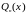многочлен той же степени , коэффициенты которого нужно будет определить. б) Если 0 является корнем характеристического уравнения, кратности к = 1,2, то частное решение можно найти в видеy _ч = x ^k Q_n(x).

2. Пусть f (x) = P_n(x) e^{ x},

где P_n(x) многочлен n-ой степени.

а) Если 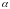не является корнем характеристического уравнения, то частное решение можно найти в таком же виде

y _ч = Q_n(x) e^{ x},где многочлен той же степени , коэффициенты которого нужно будет найти.

б) Если является корнем характеристического уравнения, кратности к = 1,2, то частное решение можно найти в виде

y _ч = x ^k Q_n(x) e^{ x}.Пример. Решить уравнение: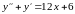 . (17)

Найдем сначала общее решение однородного уравнения

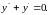
Имеем: k ² + k = 0, k ₁ = 0, k ₂ =-1, Y = C ₁+ C₂ e ^-x.

Заметим, что 0 является корнем характеристического уравнения. Поэтому частное решение ищем в виде: y_ч = x Q₁(x), где 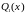многочлен первой степени, то есть 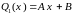. Поэтому y _ч = Аx² + B x. Чтобы найти A и B, подставим y _ч в (17): 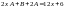.Приравняем коэффициенты при одинаковых степенях х:

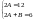
Отсюда А=6; В=-6.

Ответ: y = C₁ + C₂ e ^-x + 6 x ² - 6x общее решение. 3. Пусть

f(x) = e^{ x}(P₁(x) Cos  x + P₂(x) Sin  x). (18)Здесь P₁(x), P₂(x) многочлены, 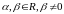и старшая степень многочленов P₁(x), P₂(x) равна n.Рассмотрим комплексное число 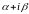.а) Если не является корнем характеристического уравнения, то частное решение можно найти в виде y_ч= e^{ x}(Q₁(x) cos  x + Q₂(x) sin  x). (19)б) Если корень характеристического уравнения, то

y_ч= x e^{ x}(Q₁(x) cos  x + Q₂(x) sin  x). (20) Здесь многочлены степени n с неопределенными коэффициентами. аметим, что если в (18) P₁(x) = 0 или P₂(x) = 0, все равно в формулах (19), (20) надо брать оба многочлена и.