2.Дифференциальные уравнения с разделяющимися переменными
Определение.
Дифференциальным уравнением с
разделяющимися переменными называется
уравнение вида
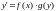В
дальнейшем будем предполагать, что
функции
и
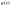непрерывны в промежутках
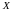и
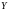соответственно.Заметим, что правая
часть уравнения (1) равна произведению
функции, зависящей только от
,
на функцию, зависящую от
.
Теорема 1.
В области, где
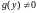, общий интеграл уравнения (1) задается
равенством
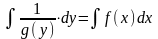(2)
Замечание
1.
Равенство (2) эквивалентно соотношению
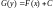
с
произвольной константой
,
где
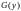и
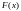есть первообразные функци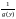й
и
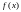соответственно.Замечание
2.
Области где
,
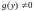есть прямоугольники (или в зависимости
от
,
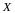полосы или полуполосы)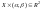
,
где
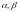либо соседние нули функции
,
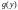либо граничные точки промежутка
.Из
теоремы 1 следует такой план решения
уравнения (1):Решить алгебраическое
уравнение
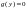(4)
и получить частные решения уравнения (1)
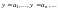(5)
где
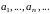корни уравнения (4)
В областях, где
,
уравнение (1) преобразовать так:
,
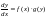‘разделить’ переменные :
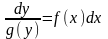
(6)
и
получить общий интеграл (2), а затем
(3).Записать в ответ:а) либо общее решение,
полученное из равенства (3), либо общий
интеграл (3); б) особые решения из
семейства (5) (не входящие в (3)). Замечание.
Равенство (6) нужно рассматривать как
равенство дифференциалов с функцией
,
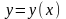являющейся решением уравнения (1).Пример
1.
Решить уравнение
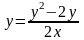(7)
Это уравнение с разделяющимися переменными, где
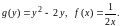
Решим уравнение (7) по плану.
Найдем корни
.
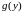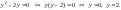
Следовательно,
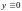и
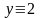есть частные решения (7) при
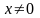.2)
В области, где
,
разделим переменные: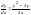
;
;
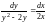3. Однородные уравнения
Определение.
Однородным дифференциальным уравнением
первого порядка называется уравнение
вида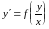
.
(1)
Пример.
Уравнение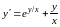
.
(2)
является
однородным. Здесь
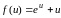.Однородное
уравнение (1) сводится к уравнению с
разделяющимися переменными. Для
этого нужно ввести новую неизвестную
функцию
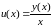В
дальнейшем будем писать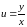
.
(3)Отсюда
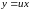и
.
(4).Подставив эти
значения
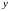и
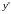в (1), получим уравнение относительно
новой искомой функции
:
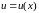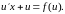Отсюда
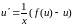(при
).
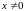А это есть уравнение с разделяющимися переменными.
Пример 1. Решим уравнение (2). Подставим (4) в (2):
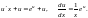
Это
уравнение с разделяющимися переменными.
Решим его по плану. Так как
,
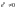то "разделяем" переменны
.
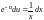Интегрируем: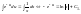
Отсюда
и из (4) получим общее решение уравнения
(2):
.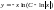