
- •2. Общее и частное решение.
- •2.Дифференциальные уравнения с разделяющимися переменными
- •Это уравнение с разделяющимися переменными, где
- •3. Однородные уравнения
- •4. Линейные уравнения и уравнения Ьернулли.
- •5. Экономическая модель Эванса
- •6.Экономическая модель Соллоу. Золотое правило экономики
- •7. Дифференциальные уравнения второго порядка. Понижение порядка. Примеры.
- •2. Дифференциальные уравнения второго порядка, которые приводятся к уравнениям первого порядка.
- •Это уравнение приводится к уравнению (n-k)-го порядка
- •8. Линейные дифференциальные уравнения второго порядка. Пространство решений. Фундаментальная система решений.
- •9. Неоднородные линейные дифференциальные уравнения второго порядка.
- •10. Числовые ряды. Сумма рде и се свойства. Необходимое условие сходимости. Геометрическая прогрессия
- •11. Ряды со знакопеременными членами. Абсолютная сходимость. Пришак Лейбница
- •12. Ряды со знакопеременными членами. Абсолютная сходимость. Пришак Лейбница
- •13. Функциональные рядЫ. При шахи Коши и Даламбсра для знакопеременных рядов.
- •14. Степенные ряды. Радиус и интервал сходимости. Формула Коши и Даламбсра для радиуса сходимости
- •15. Свойства степенных рядов. Разложение функции в ряд Тейлора
- •17.Комплексные числа.Операции над ними.
- •18. Тригонометрическая форма записи. Умножение и деление в тригонометрической форме. Формула Муавра. .
7. Дифференциальные уравнения второго порядка. Понижение порядка. Примеры.
Определение 1. Обыкновенным дифференциальным уравнением второго порядка называют соотношение вида:
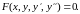 (1)
(1)
Уравнение вида
 (2)называется
дифференциальным уравнением второго
порядка, разрешенным относительно
старшей производнойЗадача Коши для
дифференциального уравнения второго
порядка ставится так:
(2)называется
дифференциальным уравнением второго
порядка, разрешенным относительно
старшей производнойЗадача Коши для
дифференциального уравнения второго
порядка ставится так:
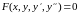
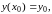 (3)
(3)
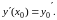 (4)
(4)
Здесь
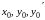 - заданные числа, которые называются
начальными данными.Геометрический
смысл задачи Коши (1), (3), (4) состоит в
нахождении решения
- заданные числа, которые называются
начальными данными.Геометрический
смысл задачи Коши (1), (3), (4) состоит в
нахождении решения
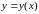 уравнения (1), график которого проходит
через данную точку
уравнения (1), график которого проходит
через данную точку
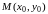 и касательная к графику решения в точке
и касательная к графику решения в точке
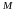 имеет заданный коэффициент наклона
имеет заданный коэффициент наклона
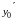 .Теорема
существования и единственности для
задачи Коши (2), (3), (4) формулируется
аналогично соответствующей теореме
для уравнения первого порядка.Пусть
.Теорема
существования и единственности для
задачи Коши (2), (3), (4) формулируется
аналогично соответствующей теореме
для уравнения первого порядка.Пусть
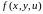 есть функция трех переменных,
соответствующая правой части уравнения
(2)Теорема.
Если функции
есть функция трех переменных,
соответствующая правой части уравнения
(2)Теорема.
Если функции
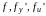 непрерывны в некоторой области
непрерывны в некоторой области
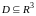 ,
то для любой точки
,
то для любой точки
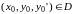 задача Коши (2), (3), (4) имеет единственное
решение
,
определенное в некоторой окрестности
точки
задача Коши (2), (3), (4) имеет единственное
решение
,
определенное в некоторой окрестности
точки
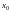 .Единственность
решения понимается в том же смысле как
для уравнения 1го
порядка.
.Единственность
решения понимается в том же смысле как
для уравнения 1го
порядка.
2. Дифференциальные уравнения второго порядка, которые приводятся к уравнениям первого порядка.
Один из способов решения дифференциальных уравнений второго и высших порядков состоит в понижении порядка уравнения.Рассмотрим два типа уравнений 2го порядка, которые с помощью подходящей подстановки, приводятся к уравнениям первого порядка.
1).Уравнение вида
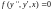 ,
(1)
,
(1)
не
содержащее явным образом
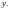 Введем
функцию p=y=y(x).
Тогда
y=p.
Подставив эти значения y
и y
в (1), получим уравнение 1го
порядка относительно функции p:
Введем
функцию p=y=y(x).
Тогда
y=p.
Подставив эти значения y
и y
в (1), получим уравнение 1го
порядка относительно функции p:
f(p,p,x)=0 . (2)
Если из уравнения (2) удастся найти все решения p=p(x), то проинтегрировав их, найдем все решения уравнения (1).Замечание. Аналогично понижается порядок у уравнения nго порядка вида:
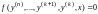 ,
,
которое не содержит искомой функции y и её производных до порядка (к-1).
Это уравнение приводится к уравнению (n-k)-го порядка
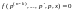
с
помощью замены
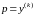 .
.
Уравнение вида :
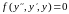 ,
(3)не содержащее
явным образом x.
,
(3)не содержащее
явным образом x.
Для
решения введем также функцию:
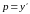 (4)
(4)
Только теперь аргументом функции р будет y, то есть:p=p(y). (5)
Тогда по правилу дифференцирования сложной функции получим:
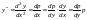 ,
,
То
есть
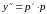 .
(6)
.
(6)
Подставив (4),(6) в (3), получим уравнение
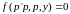 ,
(7)
,
(7)
являющееся
уравнением первого порядка относительно
функции (5).Теперь для того, чтобы из
решения
p = p(y)
уравнения (7) получить решение у=y(x)
уравнения (3) нужно решить ещё одно
уравнение 1го
порядка:
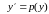 которое является уравнением с
разделяющимися переменными.
Замечание.
Аналогично, с помощью подстановки
(4)-(6) понижается порядок уравнения вида:
которое является уравнением с
разделяющимися переменными.
Замечание.
Аналогично, с помощью подстановки
(4)-(6) понижается порядок уравнения вида:
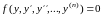 .
.
Пример 1. Решить уравнение:
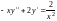 .
.
Это
уравнение не содержит y.
Полагая
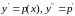 ,
получим линейное уравнение 1го
порядка:
,
получим линейное уравнение 1го
порядка:
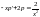 .
(8)
.
(8)
Решение
его ищем по известному методу в виде: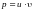 .После подстановки в (8) получим:
.После подстановки в (8) получим:
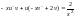 .
(9)
.
(9)
Функцию
подберем из уравнения:
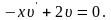 После
“разделения переменных” из соотношения
После
“разделения переменных” из соотношения
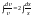 найдем ненулевое частное решение:
найдем ненулевое частное решение:
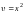 .
Тогда уравнение (9) примет вид
.
Тогда уравнение (9) примет вид
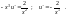
Отсюда
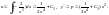
Проинтегрировав, получим общее решение исходного уравнения:
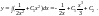
Пример 2. Решить задачу Коши.

В
это уравнение не входит x.
Порядок уравнения понизим с помощью
подстановки: y’=p
, где p=p(y).
Тогда согласно (6),
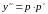 и исходное уравнение примет вид:
и исходное уравнение примет вид:
 1.
Случай: p=0.
Отсюда
1.
Случай: p=0.
Отсюда
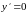 , то есть y=C=const.2.
Случай: p0
, тогда p’tg
y=2p.Это
уравнение с разделяющимися переменными
относительно функции p=p(y).Разделим
переменные:
, то есть y=C=const.2.
Случай: p0
, тогда p’tg
y=2p.Это
уравнение с разделяющимися переменными
относительно функции p=p(y).Разделим
переменные:
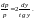 Проинтегрируем это равенство :
Проинтегрируем это равенство :
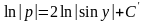 ,
где
,
где
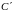 =const.
=const.
