Ь а1. Определение дифференциального >равнения первою порядка и его геометрический смысл. Задача Коши. Общее и частное решение. Особое решение. Пример. Общий и частный интеграл,

Определение 1 . Обыкновенным дифференциальным уравнением первого порядка называется соотношение вида

F(x,y,y)=0. (1)

Решением этого уравнения называется функция y=y(x), определенная и дифференцируемая на интервале X (конечном или бесконечном) так

F(x, y(x), y (x))= 0  x X.

Решить уравнение - значит найти все его решения. Нахождение решений дифференциального уравнения называют интегрированием этого уравнения.

Определение 2. Уравнение у = f (x, y) называется дифференциальным уравнением первого порядка, разрешенным относительно производной.Пример. Закон Уокена в экономике описывается дифференциальным уравнением

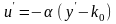.Здесь 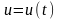есть количество безработных, 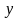есть валовый продукт, который может быть выражен производственной функцией Кобба-Дугласа, 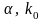есть некоторые константы.Теорема 1. (существования и единственности).Если f (x, y) и f _y (x, y) непрерывны в области D  R² , то для любой точки

( x₀ ,y₀ ) D существует единственное решение y =y ( x ) задачи

у = f (x, y) (2)

у (x₀ ) = y₀ , (3)

определенное на некотором интервале, содержащем x₀ .Замечание. Единственность означает, что любые два решения задачи (2), (3) совпадают в некоторой окрестности точки x₀ .Определение 3. Задача (2) - (3) называется задачей Коши.Определение 4. Пусть y = y₁ (x) и y = y₂ (x) ecть два решения задачи (2), (3),определенные на интервалах X₁ , X₂ соответственно таких, что

X₁  X₂ и y₁ (x)= y₂ (x)  x  X₁ .

Тогда решение y = y₂ (x) называется продолжением решения y = y₁ (x).

Определение 5. Решение, не имеющее продолжения, называется непродолжаемым.Теорема 2. Если выполнены условия теоремы 1, то любое решение задачи (2), (3) продолжается до непродолжаемого единственным образом.

Определение 6. Интегральной кривой называется график непро-должаемого решения.

2. Общее и частное решение.

Рассмотрим пример простейшего дифференциального уравнения

y = x² (4)

Решая его, получим 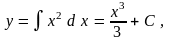где CR - произвольная постоянная. Равенство

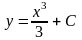(5)

задает семейство функций с параметром C, которое является множеством всех решений уравнения (4) Из (5) также следует, что интегральными кривыми уравнения (4) являются кубические параболы , полученные из параболы y = x³ cдвигом вдоль оси Oy. Определение 1. Однопараметрическим семейством функций называется множество функций вида y =  (x,С). При этом С называется параметром данного семейства. Множество значений, которое может пробежать параметр С, будем называть множеством допустимых значений параметра С. Определение 2. Пусть в области D R² выполнены условия теоремы 1 (существования и единственности). Общим решением уравнения (2) в области D называется однопараметрическое семейство функций y =  (x, С) (6)

такое, что а) при любом фиксированном допустимом значении параметра С функция (6) является решением (2) и ее график лежит в D.б) любое решение уравнения (2), график которого лежит в D, входит в семейство (6). Замечание. Как правило, общее решение составляет все множество решений дифференциального уравнения за некоторым, быть может, исключением.Определение 3. Решение, не входящее в общее решение, то есть не являющееся членом семейства (6) ни при каком С , называется особым решением.

Пример. Рассмотрим уравнение

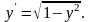
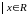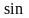Условия теоремы существования и единственности для него выполнены в области D = {(x , y) , -1< y < 1}. Общим решением этого уравнения является семейство синусоид y = (x + C), определенных на интервале

( - С -  /2 , - C +  /2 ). (Это легко проверить

подстановкой). Кроме того, имеются два

особых решения y  1 и y  -1. Заметим, что на прямых y =  1 нарушаются условия теоремы 1.Определение 4. Если в общем решении (6) параметру С придать определенное значение С=С₀, то решение y =  (x, C₀ ) называется частным решением (1).Определение 5. Равенство вида Ф( x, y, C) = 0, неявно задающее общее решение, называется общим интегралом дифференциального уравнения. Соотношение Ф(x, y, C₀ )= 0 называется частным интегралом. Линии, задаваемые общим интегралом, также называются интегральными кривыми.Геометрический смысл дифференциального уравнения.Если функция f (x,y) определена в области D R² , то уравнение y = f (x, y) (7) задает в любой точке области D значение углового коэффициента касательной к проходящему через эту точку графику решения уравнения (7).Зададим в каждой точке (x,y) D направление касательной с помощью отрезка, тангенс угла наклона которого к оси Ox равен f (x, y). Построенное множество отрезков называется полем направлений уравнения (7).Геометрически решить уравнение (7) означает, что требуется найти кривую y =  (x), которая в любой своей точке касается отрезка из поля направлений.