
- •Ответы на вопросы по Математическому Анализу (II семестр)
- •4) Определенный интеграл Риммана.
- •10) Несобственный интеграл II-ого рода (от разрывной функции)
- •11) Теоремы сравнения.
- •12) Несобственный интеграл( общий случай)
- •13) Примеры применения определенных интегралов.
- •14) Интегралы от четных и нечетных функций, на симметричных приделах интегрирования
- •15) Гамма-функция, бета-функция:
- •16) Сходимость числового ряда.
- •17) Признак сравнения рядов.
- •18) Абсолютная сходимость
- •19) Радикальный признак сходимости Коши
- •20) Признак сходимости Деламбера.
- •21) Признак Лейбница
- •22) Интегральный признак сходимости (Коши).
- •23) Степенные ряды, теорема Абеля:
- •27) Вещественное значение ряда Фурье
- •29) Разложение четных и нечетных функций:
21) Признак Лейбница
![]() (1)
(1)
Если последовательность абсолютных(|un|)
величин монотонно убывает (u1>u2>u3>…un>…)
и стремиться к нулю (![]() )
то ряд (1) сходится при этом сумма S
ряда удовлетворяет 0<S<u1
)
то ряд (1) сходится при этом сумма S
ряда удовлетворяет 0<S<u1
Рассмотрим сначала частичную сумму четного числа (2n) числового ряда:
![]() согласно первому условию теоремы
выражение в скобках всегда положительно
и значит сумм S2n>0
и возрастает с возрастанием номера 2n
с другой стороны последовательность
S2n
можно переписать так:
согласно первому условию теоремы
выражение в скобках всегда положительно
и значит сумм S2n>0
и возрастает с возрастанием номера 2n
с другой стороны последовательность
S2n
можно переписать так:
![]() легко видеть что S2n<u1
таким образом последовательность S2,
S4, S6,
…, S2n,
… возрастает и ограничена сверху,
т.е. имеет придел
легко видеть что S2n<u1
таким образом последовательность S2,
S4, S6,
…, S2n,
… возрастает и ограничена сверху,
т.е. имеет придел
![]() ,
причем 0<S2n<u1
рассмотрим теперь частичные суммы
нечетного числа (2n+1)
очевидно что S2n+1=S2n+u2n+1
следовательно
,
причем 0<S2n<u1
рассмотрим теперь частичные суммы
нечетного числа (2n+1)
очевидно что S2n+1=S2n+u2n+1
следовательно
![]() (
(![]() по
второму условию теоремы)
по
второму условию теоремы)
И так:
![]() при
четном и нечетном n
следовательно ряд (1) сходится причем
0<S<u1/чтд
при
четном и нечетном n
следовательно ряд (1) сходится причем
0<S<u1/чтд
Замечание Исследование знакочередующегося ряда с отрицательным первым членом сводится к исследованию ряда (1) путём умножения каждого члена исходного ряда на -1.
22) Интегральный признак сходимости (Коши).
Если члены знакоположительного ряда
(2)
могут быть представлены как числовые
значения некоторой непрерывной монотонно
убывающей на промежутке [1;+∞) функции
f(x) так, что
u1=f(1), u2=f(2),
…, un=f(n),
…, то если сходится (расходится) интеграл
![]() сходится, то сходится(расходится) и ряд
(2)
сходится, то сходится(расходится) и ряд
(2)
Доказательство:
р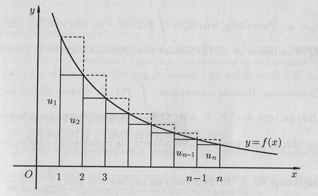 ассмотрим
криволинейную трапецию, ограниченную
сверху графиком функции y=f(x),
основанием которой служит отрезок оси
Ox от x=1 до
x=n, строим
входящие и выходящие прямоугольники,
основаниями которых служат отрезки[1;2],
[2;3] … [n-1;n] … Учитывая
геометрический смысл определенного
интеграла, запишем:
ассмотрим
криволинейную трапецию, ограниченную
сверху графиком функции y=f(x),
основанием которой служит отрезок оси
Ox от x=1 до
x=n, строим
входящие и выходящие прямоугольники,
основаниями которых служат отрезки[1;2],
[2;3] … [n-1;n] … Учитывая
геометрический смысл определенного
интеграла, запишем:
![]()
Или
![]() т.е.
т.е.
![]()
Случай когда несобственный интеграл
![]() =A>
=A>![]() сходится, то получаем
сходится, то получаем
![]() так как последовательность частичных
сумм монотонно возрастает и ограничена
сверху числом (A+u1),
то по признаку существования придела
имеет придел следовательно ряд сходится.
так как последовательность частичных
сумм монотонно возрастает и ограничена
сверху числом (A+u1),
то по признаку существования придела
имеет придел следовательно ряд сходится.
Случай когда несобственный интеграл
=+∞
и интегралы
неограниченно возрастают при
![]() учитывая что
учитывая что
![]() получается
что
получается
что
![]() при
т.е. ряд расходится.
при
т.е. ряд расходится.
Замечание: вместо интеграла
можно брать
![]() где
k >1
где
k >1
23) Степенные ряды, теорема Абеля:
1)![]()
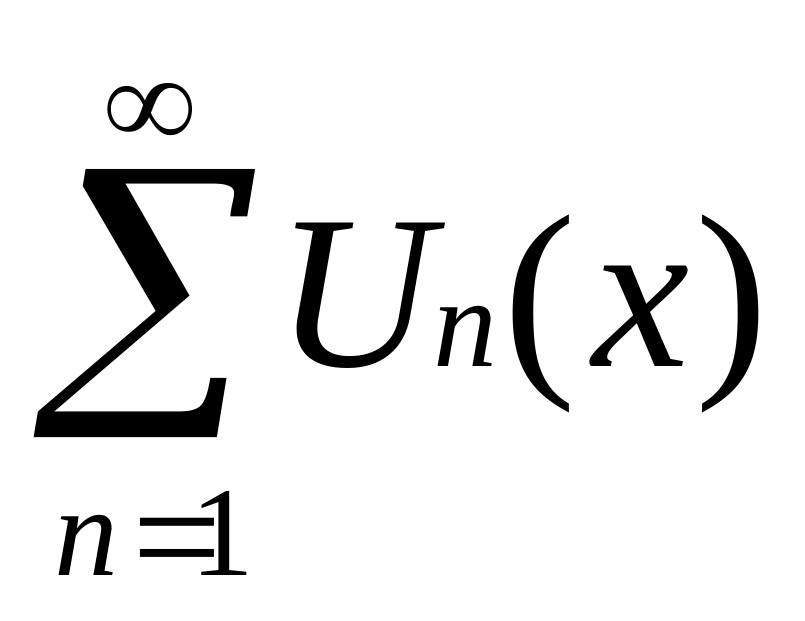 - функциональный ряд. Множество значений
x, при которых ряд
сходится, называется областью сходимости
ряда.
- функциональный ряд. Множество значений
x, при которых ряд
сходится, называется областью сходимости
ряда.
![]() -
сходится при lxl<1
– область сходимости;
-
сходится при lxl<1
– область сходимости;
![]() -
- сходится при x<0 –
область сходимости;
-
- сходится при x<0 –
область сходимости;
2)Ряд вида
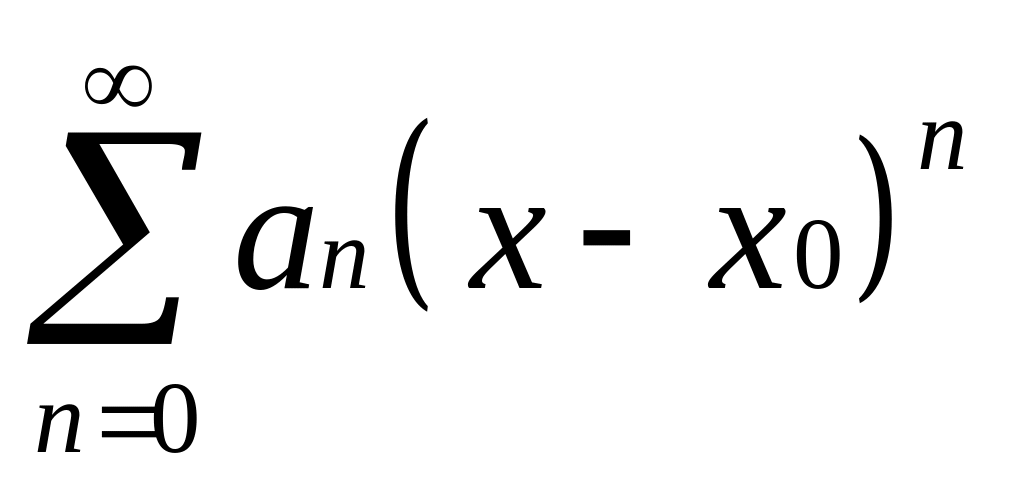 - (1) - степенной ряд
- (1) - степенной ряд
![]() ,
,
![]() - компл.значное число
- компл.значное число
Теорема Абеля:
Если ряд (1) сходится при х=х1,
то он сходится абсолютно и при любом
значении х2 , удовлетворяя
неравенству
![]() (т.е. ближе к х0 или к х1)
при любом х2.
(т.е. ближе к х0 или к х1)
при любом х2.
Док-во:
![]() -
разделим и умножим на
-
разделим и умножим на
![]()
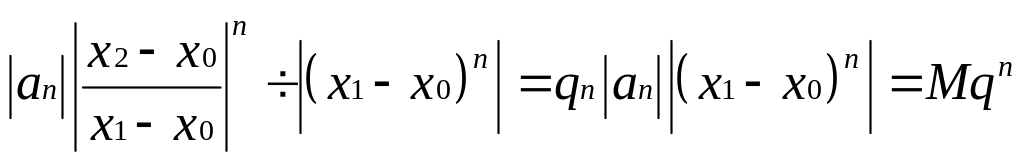 (Причем
(Причем
![]() - огранич.,т.к.
- огранич.,т.к.
![]() сходится и общий член стремится к нулю.)
< = M
сходится и общий член стремится к нулю.)
< = M
![]()
ряд сходится.
Если расходится ряд
![]() расходится при х=
расходится при х=![]() :
:
![]() (ближе к х0 чем к х3)
(ближе к х0 чем к х3)
Областью сходимости степенного ряда
является интервал
![]() <R.
R – радиус сходимости
степенного ряда.
<R.
R – радиус сходимости
степенного ряда.
Основные свойства степенных рядов:
1. Сумма S(x)
степенного ряда
![]() является непрерывной функцией в интервале
сходимости (-R;R).
является непрерывной функцией в интервале
сходимости (-R;R).
2. Степенные ряды
и
![]() ,
имеющие радиусы сходимости соответственно
R1 и R2, можно
почленно складывать, вычитать и умножать.
Радиус сходимости произведения, суммы
и разности рядов не меньше, чем меньшее
из чисел R1 и R2.
,
имеющие радиусы сходимости соответственно
R1 и R2, можно
почленно складывать, вычитать и умножать.
Радиус сходимости произведения, суммы
и разности рядов не меньше, чем меньшее
из чисел R1 и R2.
3. Степенной ряд внутри интервала сходимости можно почленно дифференцировать; при этом для ряда S(x)=a0+a1x+a2x2+a3x3+…+anxn+…при –R<x<R выполняется равенство S’(x)=a1+2a2x+3a3x2+…+nanxn+…
4. Степенной ряд можно почленно интегрировать на каждом отрезке, расположенном внутри интервала сходимости; при этом для ряда S(x)=a0+a1x+a2x2+a3x3+…+anxn+… при
–R<a<x<R
выполняется равенство
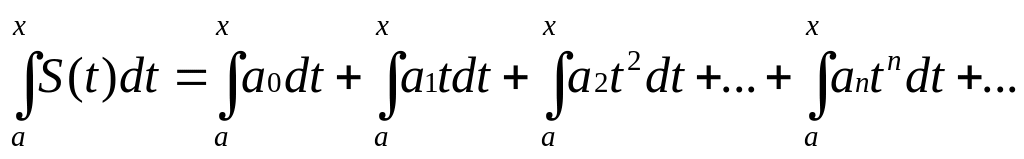
Ряды S’(x)=a1+2a2x+3a3x2+…+nanxn+… и имеют тот же радиус сходимости, что и исходный степенной ряд.
24) Ряд Тейлора (ex, sinx, cosx, (1+x)a, ln(1+x))
Степенные ряды можно почленно дифференцировать и интегрировать внутри интервала сходимости.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
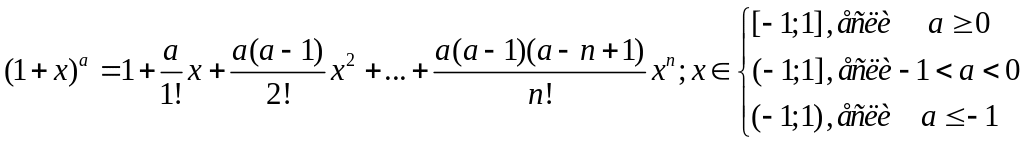
![]() ,
,
![]()
25, 26) ряд Фурье, Ортогональность
системы ф-ции![]() ,
Ряд Фурье в комплексной форме.
,
Ряд Фурье в комплексной форме.
Ряд Фурье:
![]()
Из алгебры:
![]() -
любое линейное пространство (но
-
любое линейное пространство (но
![]() попарно перпендикулярны)
попарно перпендикулярны)
![]()
![]()
![]()
![]() (коэффиценты Фурье)
(коэффиценты Фурье)
![]()
![]()
![]()
![]()
(обобщенный ряд Фурье для f)
Ортогональность системы фунции :
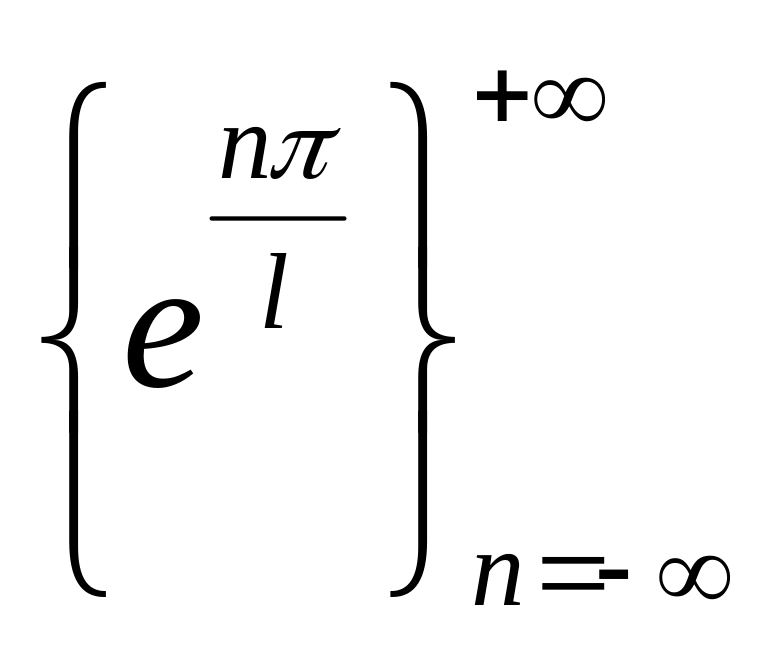 (*)
(*)
Ряд Фурье в комплексной форме:
![]() для комплексного значения
для комплексного значения
![]() - если представить, то получится
комплексно сопряженное
- если представить, то получится
комплексно сопряженное
(пределение скалярного произведения.)
Надо доказать, что скалярное произведение любых 2-х функций = 0, то есть они попарно перпендикулярны.
![]()
n, m- натуральные числа
l- конкретное заданное число в [-l;l]- (*) будут попарно перпендикулярны.
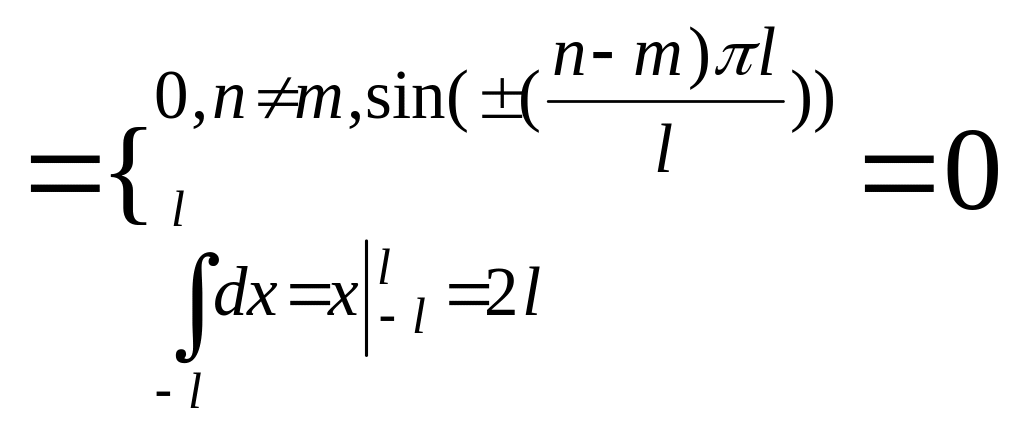

Запишем для какой-либо ф-ии ряд Фурье:
![]() -сумма
ряда
-сумма
ряда
![]() -
ряд Фурье
-
ряд Фурье
Пусть функция f(x) имеет 2l и кусочно непрерывна (на любом конечном интервале имеет не более чем конечное число точек разрыва), кусочно монотонна, тогда имеет место равенство:
![]()
