
- •Ответы на вопросы по Математическому Анализу (II семестр)
- •4) Определенный интеграл Риммана.
- •10) Несобственный интеграл II-ого рода (от разрывной функции)
- •11) Теоремы сравнения.
- •12) Несобственный интеграл( общий случай)
- •13) Примеры применения определенных интегралов.
- •14) Интегралы от четных и нечетных функций, на симметричных приделах интегрирования
- •15) Гамма-функция, бета-функция:
- •16) Сходимость числового ряда.
- •17) Признак сравнения рядов.
- •18) Абсолютная сходимость
- •19) Радикальный признак сходимости Коши
- •20) Признак сходимости Деламбера.
- •21) Признак Лейбница
- •22) Интегральный признак сходимости (Коши).
- •23) Степенные ряды, теорема Абеля:
- •27) Вещественное значение ряда Фурье
- •29) Разложение четных и нечетных функций:
10) Несобственный интеграл II-ого рода (от разрывной функции)
Пусть функция f(x)
непрерывна на промежутке [a;b)
и имеет бесконечный разрыв при x=b.
Если существует конечный придел
![]() то его называют несобственным интегралом
первого рода и записывают как:
то его называют несобственным интегралом
первого рода и записывают как:![]() т.е.
=
т.е.
=
Если придел существует, то интеграл сходится, если не существует или бесконечен, то расходится.
Аналогично если функция терпит разрыв
в точке x=a
то полагают
=![]() Если же функция терпит разрыв во
внутренней точке с отрезка [a;b],
то несобственный интеграл второго рода
определяется формулой:
Если же функция терпит разрыв во
внутренней точке с отрезка [a;b],
то несобственный интеграл второго рода
определяется формулой:
![]()
Признаки сходимости:
1. Пусть на промежутке [a;b)
функция f(x)
и g(x)
непрерывны, при x=b
терпят бесконечный разрыв и удовлетворяют
условию
из
сходимости
![]() вытекает сходимость
,
а из расходимости
расходимость
вытекает сходимость
,
а из расходимости
расходимость
![]()
2. Пусть на промежутке [a;b) функция f(x) и g(x) непрерывны, при x=b терпят бесконечный разрыв. Если существует придел , то интегралы и сходятся или расходятся одновременно.
11) Теоремы сравнения.
(1)
![]() ,
f и g
непрерывны в [a,b],
за исключ т С
,
f и g
непрерывны в [a,b],
за исключ т С
![]()
![]()
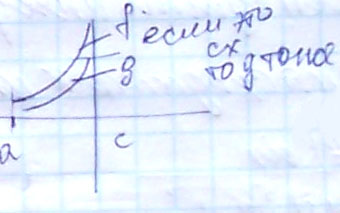
Если сх (1), то сх и (2)
(1)![]() (2)
(2)
![]()
(2) расх, то и (1) расх
(2)
![]()
![]()
![]()
![]()
Если
![]() ,
то (1) и (2) сходятся или расходятся
одновременно
,
то (1) и (2) сходятся или расходятся
одновременно
12) Несобственный интеграл( общий случай)
![]()
Точки
![]() -точки
разрыва f(x)
-точки
разрыва f(x)
![]()
![]()
Для того, чтобы сходился этот интеграл, необходимо, чтобы сходились:
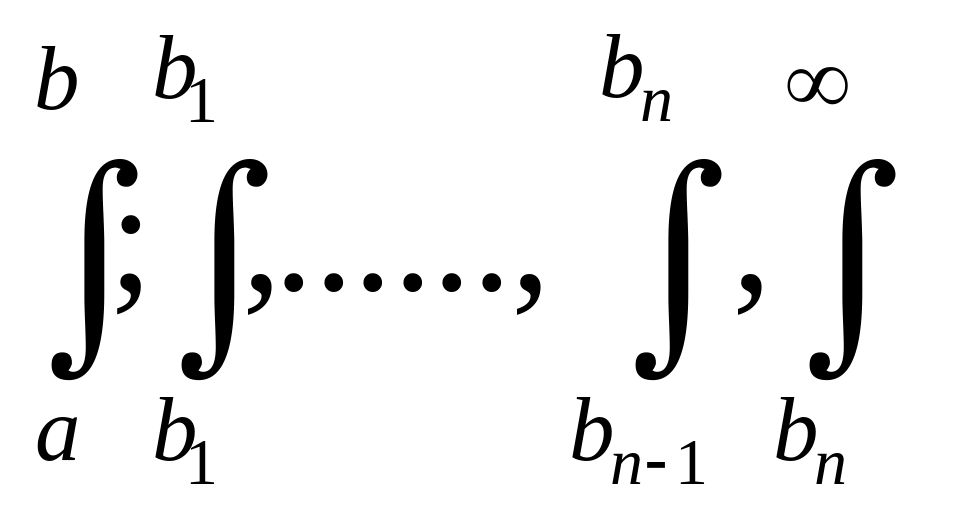
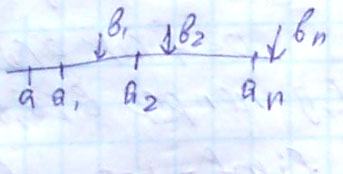
Тот интеграл равен сумме интегралов.
13) Примеры применения определенных интегралов.
В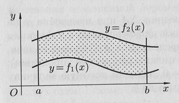 ычисление
площадей плоских фигур S=
или S=
ычисление
площадей плоских фигур S=
или S=
![]() ,
доказывается легко по определению
определенного интеграла. Площадь плоской
фигуры ограниченной двумя функциями
как на рисунке ищется по формуле
,
доказывается легко по определению
определенного интеграла. Площадь плоской
фигуры ограниченной двумя функциями
как на рисунке ищется по формуле
S=![]() -
-![]() =
=![]()
Д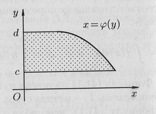 оказывается
легко площадь искомой фигуры можно
получить путём вычитания из площади
трапеции образованной верхней функцией,
площади трапеции образованной нижней
функцией.
оказывается
легко площадь искомой фигуры можно
получить путём вычитания из площади
трапеции образованной верхней функцией,
площади трапеции образованной нижней
функцией.
S=![]()
Если кривая задана параметрически
![]()
![]()
В полярных координатах площадь
криволинейного сектора S=![]()
Вычисление длины дуги плоской кривой
Прямоугольные координаты: Под длиной дуги AB принимается придел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной неограниченно возрастает, а длина наибольшего её звена стремиться к нулю.
![]()
Если заданно параметрически то
![]()
Полярные координаты:
![]()
Объем тела:
![]()
Объем тела вращения:
![]()
14) Интегралы от четных и нечетных функций, на симметричных приделах интегрирования
Если f(x)
четная функция от f(-x)=f(x).
Так как
![]() ,
а
,
а
![]()
Т.е.
![]()
Если f(x) нечетная функция то f(-x)=-f(x) Так как , а
![]()
Т.е.
![]()
15) Гамма-функция, бета-функция:
1) Гамма-функция – функция вида
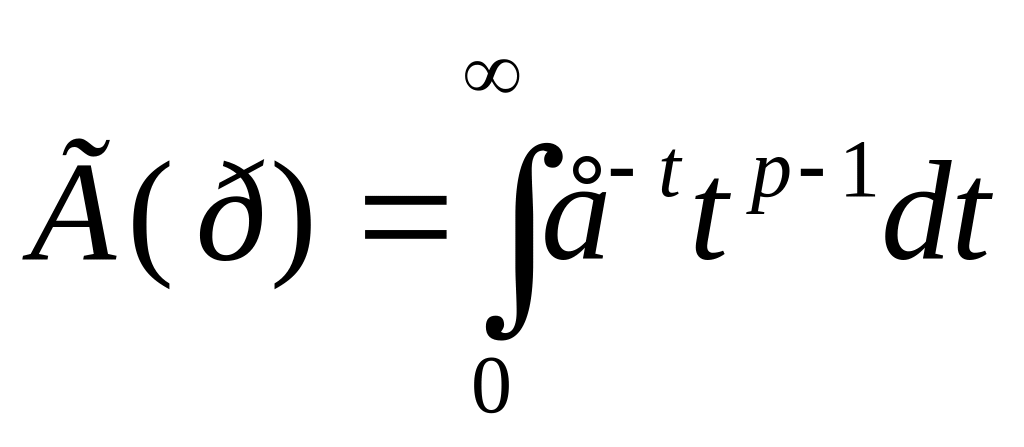 (р>0,
если р – комплексное число, то Rep>0)
(р>0,
если р – комплексное число, то Rep>0)
При p=1:
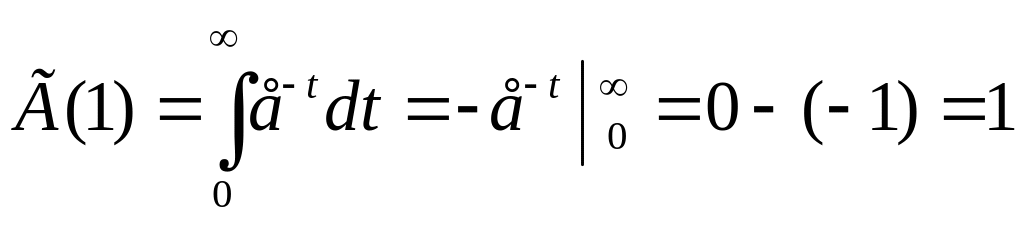
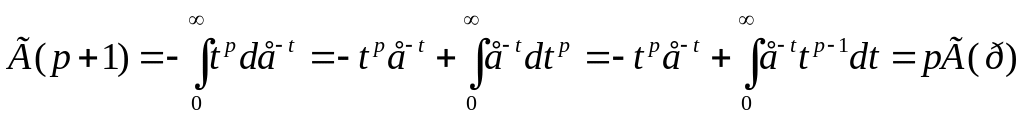
Г(n+1)= (где n
– натуральное число)![]()
2) Бета-функция q,p>0
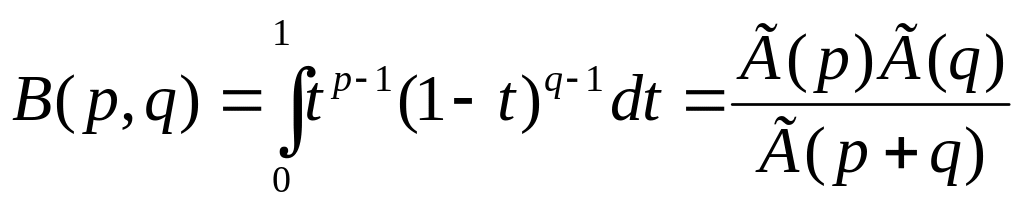 B(p,q)=B(q,p)
B(p,q)=B(q,p)
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
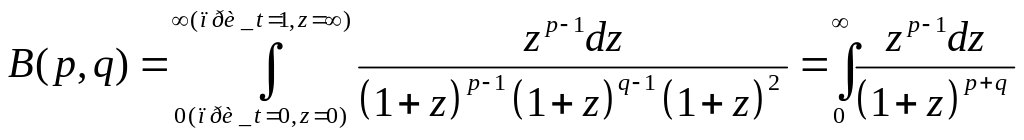
16) Сходимость числового ряда.
Числовой ряд:
![]() где
u1 u2
…un…
члены ряда, un
общий член ряда сумма первых n
членов ряда, называется n-ой
частичной суммой ряда и обозначается
где
u1 u2
…un…
члены ряда, un
общий член ряда сумма первых n
членов ряда, называется n-ой
частичной суммой ряда и обозначается
Sn=u1+u2+…+un,
если существует конечный придел
S=![]() последовательности
частичных сумм ряда, то этот придел
называют суммой ряда и говорят что ряд
сходится. Записывают S=
последовательности
частичных сумм ряда, то этот придел
называют суммой ряда и говорят что ряд
сходится. Записывают S=![]() ,
если
не существует или
,
если
не существует или
![]() то
ряд называют расходящимся.
то
ряд называют расходящимся.
Необходимый признак сходимости: если ряд сходится, то его общий член un стремиться к нулю.
Док-во. Пусть ряд сходиться и
=
S тогда
![]() =
S (при n и
(n-1) стремящихся к
бесконечности). Учитывая что un=
=
S (при n и
(n-1) стремящихся к
бесконечности). Учитывая что un=![]() -
-![]() при n>1 получаем:
при n>1 получаем:
![]()
