- •1. Определение вероятности. 1
- •2. Условная вероятность. Независимое событие. Формула умножения вероятности.
- •4.Последовательность независимых испытаний. Схема Бернулли. Формула Пуассона.
- •Формула Пуассона
- •5.Наивероятнейшее число наступления события.
- •6. Локальн теорема и интегральная теорема Муавр- 3
- •7. Св. Функции распределения и их свойства.
- •8.Числовые хар-ки случайной величины. 4
- •9.Биномиальный закон распределения.
- •10.Распределение Пуассона. Равномерное распределение.
- •11. Показательное или экспоненциальное распределение.
- •12. Нормальный закон распределения. Числовые 6 характеристики.
- •14.Многомерные случайные величины(св)
- •15.Неравенство Маркова. Неравенство Чебышева.
- •16. Т.Чебышева. Т.Бернули. 8
- •17. Теорема Ляпунова:
- •Элементы математической статистики Генеральная выборочная совокупность
- •Повторная и бесповторная выборка
- •Репрезентативная выборка
- •Статистическое распределение выборки
- •Методы построения точечных оценок
- •Билет №1 10
- •Билет №2
- •Билет №3
- •Билет №4
- •Билет № 5
- •Билет 6.
- •Билет 7
- •Билет 8
- •Билет 9.
- •Билет 10.
- •Билет 11.
- •Билет 12.
- •Билет № 13
- •Билет 14.
- •Билет 15. 16
- •Билет 16.
- •Билет 17.
- •Билет 18.
- •Билет 19.
- •Билет 20. 18
- •Билет 27.
- •Билет 28.
- •1.Теория вероятности
- •3 Т. «Сложения вероятности несовместных событий 20
- •5Формула полной вероятности
- •6.Вероятность наступления хотя бы 1-го события
- •10Вероятность отклонения относительной частоты от постоянной вероятности
- •11Случайная величина
- •12Интегральная ф-ия распределения
- •13Дифференциальная ф-ия распределения вероятностей св (её плотность)
- •14Числовые хар-ки св
- •15Дисперсия св (дискретной)
- •16Среднеквадратическое отклонение св х –
- •17Моменты св х:
- •18Важнейшие з-ны распределения вероятностей cв:
- •21Т.Чебышева
- •22Т. Ляпунова
- •26Вероятность попадания случайной точки в полосу
- •29Числовые хар-ки 2-мерной св (с-мы св):
- •31Нормальное распределение с-мы 2-х св
15.Неравенство Маркова. Неравенство Чебышева.
Пусть
СВ X принимает только
неотрицательные значения и у неё есть
матем. Ожидание M(x),
то какова бы ни была положительная
величина ξ той же размерности, что и X,
всегда выполняется
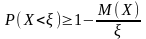 ;
;
Док-во: проведем док-во только для непрерывных СВ. P(X)=0,X<0; P(X)>=0,X>=0;
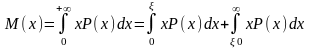 ;
;
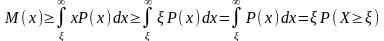 ;
;
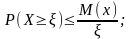
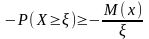 ;
;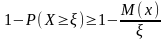 ;
.
;
.
Неравенство Чебышева.
Какаво
бы не было положительное число
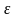 для любой СВ X, дисперсия
которой конечна справедливо неравенство
для любой СВ X, дисперсия
которой конечна справедливо неравенство
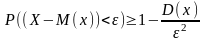 ;
;
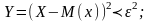
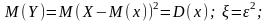
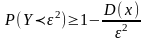 .
.
16. Т.Чебышева. Т.Бернули. 8
Последовательность
чисел
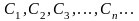 наз.
равномерно ограниченной, если сущ.
такая константа M ,
наз.
равномерно ограниченной, если сущ.
такая константа M ,
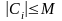 .
Если
.
Если
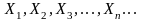 -
последовательность попарно независимых
СВ, у каждой из которых есть мат. ожидание
-
последовательность попарно независимых
СВ, у каждой из которых есть мат. ожидание
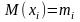 и
и
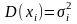 (дисперсии
равномерно ограничены), то
(дисперсии
равномерно ограничены), то
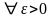 предел
предел
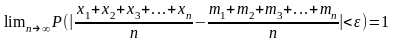 (6)
-предел по вероятности.
(6)
-предел по вероятности.
Док-во.
По условию последовательность дисперсии
равномерно ограниченна, т.е.
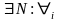 ,
,
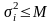 .
.
Рассмотрим
вспомогательные СВ
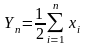 .
У нее есть мат. ожидание
.
У нее есть мат. ожидание
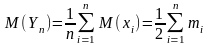
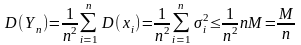
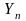 удовл. требованиям
неравенства Чебышева. Применяя
неравенство (6)
удовл. требованиям
неравенства Чебышева. Применяя
неравенство (6)
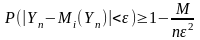 (8)
(8)
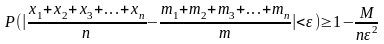 (9)
(9)
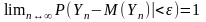
Следствие
из теоремы : если
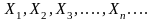 -
последов независим. СВ имеющих одно и
то же мат. ожидание
-
последов независим. СВ имеющих одно и
то же мат. ожидание
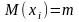 и
и
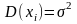 ,
то неравенство .(9). Примет вид
,
то неравенство .(9). Примет вид
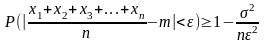 (10)
(10) 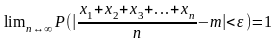
Следствие
из теоремы важно на практике, если нужно
измерить некоторую величину, истинное
значение которой
 ,
проводят
,
проводят
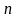 измерений этой величины. Если при
измерениях отсутствуют системные
ошибки, то
измерений этой величины. Если при
измерениях отсутствуют системные
ошибки, то
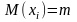 можно считать что дисперсии
можно считать что дисперсии
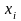 ограничены, тогда среднее арифм. значение
рез-ов измерений с ростом n
прибл. к истинному значепию измеряемой
величины m . Можно положить,
что
ограничены, тогда среднее арифм. значение
рез-ов измерений с ростом n
прибл. к истинному значепию измеряемой
величины m . Можно положить,
что
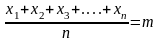 .
.
Т.Бернули
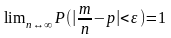 (1)
(1) 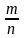 -
относительная частота или частность
(сходится к вер-ти)
-
относительная частота или частность
(сходится к вер-ти)
Док-во: Пусть - число появления события A в первом испытании.
|
0 |
1 |
|
|
q |
p |
|
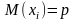 ,
,
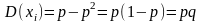
Мы находимся в условиях т.Чебышева
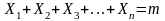 ;
;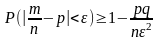
т.Бернули явл. статистическим определением вероятности.
17. Теорема Ляпунова:
Можно
доказать что, если
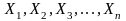 - нормально распределенные случайные
величины, то их сумма
- нормально распределенные случайные
величины, то их сумма
 также
норм. распред. СВ с мат. ожиданием
также
норм. распред. СВ с мат. ожиданием
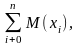
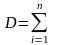 ,
,
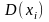
Обобщением явл. т. Ляпунова :
Пусть - независимые СВ, у каждой из которых мат. ожидание
и
,
абсолютный центральный момент третьего
порядка
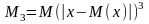 и
выполняется
и
выполняется
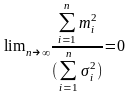 ,
.(3). то для суммы
,
.(3). то для суммы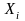 выполняется следующее
выполняется следующее
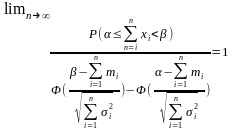 .(4).
.(4).
Следствие:
если все
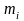 и
и
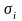 одинаковые, то
одинаковые, то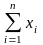 распределена
асимптотически по нормальному закону.
распределена
асимптотически по нормальному закону.
Физ.
смысл условий, при кот. сумма
будет распространяться практически
по норм закону, сост. в том, что удельный
вес каждого слаг.
должен
 0 при 9 увеличении числа слагаемых.
0 при 9 увеличении числа слагаемых.
Ошибки, допускаемые при проверке стат.гипотез.
Уровень значимости стат. критерия.
Ошибкой первого рода наз. Ошибка отклонения верной нулевой гипотезы H0
-------- второго рода наз. Принятие ложной гипотезы H0
Уровнем значимости стат. критерия наз. вероятность совершенной ошибки первого рода.
Мощностью критерия наз вероятность несовершенной ошибки второго рода.
Проверка гипотезы о нормальном распределении СВ.
Эта гипотеза есть непар. гипотеза.
Основное предположение в том, что вид закона распределения – нормальный.
Критерий
согласия
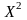 Пирсона.
Пирсона.
Пусть имеется по результатам выборки вариационный ряд.
|
X1-x2 |
X2-x3 |
X3-x4 |
… |
Xn-1-xn |
mi |
M1 |
M2 |
M3 |
… |
Mn-1 |
wi |
M1/n |
M2/n |
M3/n |
|
Mn-1/n |
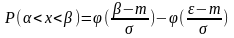
Если гипотеза о нормальном распределении верна, то эмперические частоты должны совпадать с теоритическими частотами.
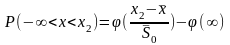 nP1-теор.частота
nP1-теор.частота
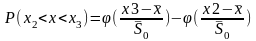 …
и т.д.
…
и т.д.
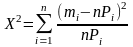 -эта
величина распространяется по закону
-эта
величина распространяется по закону
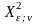 -
табличная величина.
-
табличная величина.
Если
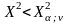 ,
гипотеза согласуется с данными опыта.
,
гипотеза согласуется с данными опыта.
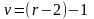 число
степеней свободы.
число
степеней свободы.
Достоинства - применим как для непрерывных, так и для дискретных СВ
Недостаток – громоздок
Эмпирическая функция распределения.
Из закона больших чисел следует, что если количество наблюдений велико, то F”(x) стремится по вероятности к теоретической функции распределения F”(x).
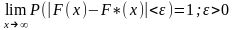
1)F”(x)-неубывающая функция.
2)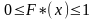
3)Если все значения находятся в промежутке [xk-1;xk] то F”(x)=1;F”(xk-1)=0;
Если по х откл.значения вариант, а по оси y накопленные частности и получаются соедин. Прямыми, то ломанные комулятой.
Комулята – статистический аналог интегральной функции распределения в теории вероятности.
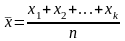 - аналог M(X);
- аналог M(X);
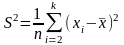 -выборочная
дисперсия.
-выборочная
дисперсия.
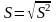 -среднее
квадратичное отклонение.
-среднее
квадратичное отклонение.
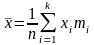

Размах
выборки
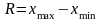
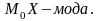 Модой
называется то значение варианты, при
котором достигается наибольшая частота.
Модой
называется то значение варианты, при
котором достигается наибольшая частота.
Если несколько таких значений – то распределение – полимодальное.
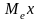 -
медиана. Делит вариационный ряд пополам.
-
медиана. Делит вариационный ряд пополам.
Начальный и центральный выборочные моменты.
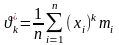
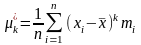
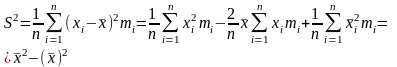
Суть метода Кормагорова: сравн. теор. и данотир. ф-цию распределения:
1)
выдвиг Ha:
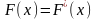 ;
;
2) извлекается выборка объема n;
3)
Находят
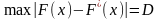
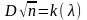 .
.
Величина
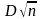 при увеличении объема выборки обладает
след. св-вом: вер-ть того, что
при увеличении объема выборки обладает
след. св-вом: вер-ть того, что
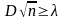 .
.
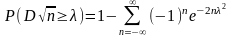 ;
;
4) по величине , сравнивая с табличными значениями в зависимости от уровня значимости
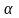 0,10 0,05 0,01
10
0,10 0,05 0,01
10
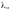 1,224 1,358 1,627
1,224 1,358 1,627
Если
окаж.
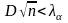 ,
то отсюда следует несоответствие
опытным данным.
,
то отсюда следует несоответствие
опытным данным.
Элементы теории корреляции.
Каждому значению х соответствует 1 или несколько вполне определенных y. Две СВ X, Y могут быть связаны, либо зависимостью другого рода, наз. Статистической, либо не связаны (независимы).
Пример: Пусть Х – кол-во внесенных удобрений, Y – урожайность с одинаковой по площади участков при одинак. внесенных удобрениях получ. различн. урожай. Средняя урожайность есть ф-ция от кол-ва удобрений.
Пусть имеется 3 участка (внесли 2 тонны). На одном получили 5 единиц, на другом 6 единиц, на 3-ем – 10 единиц.
.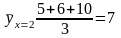
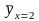 – условное среднее
– среднее арифметическое значение Y,
соотв. значению х=2. Если каждому значению
X соотв. 1 нач. условной
средней
– условное среднее
– среднее арифметическое значение Y,
соотв. значению х=2. Если каждому значению
X соотв. 1 нач. условной
средней
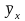 ,
то
– ф-ция от значений X. В
этом случае говорят, что СВ Y
зависит от СВ X корреляционно.
,
то
– ф-ция от значений X. В
этом случае говорят, что СВ Y
зависит от СВ X корреляционно.
Корреляционной зависимостью Y от X наз ф-цию зависимости условной средней от x.
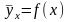 (1) это уравнение
наз. Уравнением регрессии Y
на X, а график этой ф-ции
наз. ниейрегрессии
(1) это уравнение
наз. Уравнением регрессии Y
на X, а график этой ф-ции
наз. ниейрегрессии
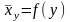 .
.