21Т.Чебышева
Пусть xk (при k=1,∞‾) – последовательность независимых СВ, у которых D(x)≤c для л. k=1,∞‾ и М(х) конечно.
Тогда ср. арифм. зн-ние этих СВ сходится по вероятности к ср. мат. ожиданию этих же величин, т.е.
limn→∞P[|1/n k=1∑nxk-1/n k=1∑nM(xk)|≥ε]=0
Док-во:
Пусть
x‾=1/n k=1∑nxk
M(x‾)=1/n∙M( k=1∑nxk‾)= 1/n k=1∑nM(xk‾)
D(x‾)=1/n2∙D( k=1∑nxk‾)=1/n2∙ k=1∑nD(xk‾)≤cn/n2=c/n
P(|x‾-M(x‾)|≥ε)≤D(x‾)/ε2 (для противоположного события)
limn→∞с/(nε2)=0 =>
limn→∞P[|1/n k=1∑nx‾k-1/n k=1∑nM(xk‾)|≥ε]=0 ч.т.д.
или для противоположного события
limn→∞с/(nε2)=0 =>
limn→∞P[|1/n k=1∑nx‾k-1/n k=1∑nM(xk‾)|<ε]=1
22Т. Ляпунова
xn (при n=1,∞‾) – последовательность независимых СВ, для каждой из к. M(xk)=mk, D(xk)=σk2, M(xk-M(x))3, кроме того
limn→∞ k=1∑n M(xk-M(x))3/( k=1∑n σk2)3/2=0, тогда при n→∞, распределение СВ Х сводится к норм. распределению.
P(x‾<x) n→∞→P =>
1/(√(2π)σx‾) -∞∫xexp(-(x‾-M(x‾))2/(2 σ2x‾))dx (без док-ва)
Т. Бернулли
Если в n независимых испытаниях появл. события А постоянно и равно Р, то отн. частота сходится по вероятности к р при n→∞
limn→∞P(|m/n-p|≤ε)=1
Док-во:
Отн. частота W(A)=m/n=1/n k=1∑nxk
M(W(A))=M(m/n)=p
По Т. Чебышева
limn→∞P(|m/n-p|≤ε)=1, ч.т.д.
Эти теоремы свидетельствуют об устойчивости частоты 25 (ср. зн-ний). З-н больших чисел даёт основание статистическому методу задания вероятности.
24С-мы СВ
н-р, 1) на пл-ти(x,y) –двумерная СВ
2)в прост-ве (x,y,z) – трехмерная СВ и т.д.
На практике чаще всего встречаются многомерные СВ, образующие с-мы СВ.
С-ма СВ(случайный вектор) – совокупность СВ, описывающая то или иное случайное событие. С-мы бывают дискретными и непрерывными.
З-ном распределения с-мы СВ наз. соотношение, устанавливающее связь между значениями СВ и их вероятностями.
С-ма, в кот. входят и дискр. и непрер. СВ, наз.смешанной.
Наиб. распр-ным распределением дискр. величины явл. таблица
xi\yj |
x1 |
x2 |
… |
xn |
y1 |
p11 |
p12 |
… |
p1n |
y2 |
p21 |
p22 |
… |
p2n |
… |
… |
… |
… |
… |
ym |
pm1 |
pm2 |
… |
pmn |
События (x=xi,y=yj), где i=1,n‾, j=1,m‾ образуют полную группу событий, сумма вероятностей к. =1
25Ф-ия распределения двумерной СВ
Ф-ией распределения с-мы СВ X и Y (двумерного случайного вектора) – вероятность совместного выполнения нер-в X<x, Y<y, т.е.
F(x,y)=P(X<x,Y<y)
Геом. смысл – вероятность попадания вектора в заданную область
Геом. смысл – неограниченный квадрат
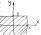
Св-ва:
1)0≤F(x,y)≤1 (по опр-нию)
2)F(x,y) неубывающая ф-ия
Док-во:
x2≥x1
P(X<x2,Y<y)=P(X<x1,Y<y)+ P(x1<X<x2,Y<y)
P(X<x2,Y<y)-P(X<x1,Y<y)=P(x1<X<x2,Y<y)≥0
для y аналогично
=>
F(x,y) – неубыв. ф-ия, ч.т.д.
3)F(-∞,y)=0 F(x,-∞)=0 F(-∞,-∞)=0 F(∞,∞)=1