
- •1. Определение вероятности. 1
- •2. Условная вероятность. Независимое событие. Формула умножения вероятности.
- •4.Последовательность независимых испытаний. Схема Бернулли. Формула Пуассона.
- •Формула Пуассона
- •5.Наивероятнейшее число наступления события.
- •6. Локальн теорема и интегральная теорема Муавр- 3
- •7. Св. Функции распределения и их свойства.
- •8.Числовые хар-ки случайной величины. 4
- •9.Биномиальный закон распределения.
- •10.Распределение Пуассона. Равномерное распределение.
- •11. Показательное или экспоненциальное распределение.
- •12. Нормальный закон распределения. Числовые 6 характеристики.
- •14.Многомерные случайные величины(св)
- •15.Неравенство Маркова. Неравенство Чебышева.
- •16. Т.Чебышева. Т.Бернули. 8
- •17. Теорема Ляпунова:
- •Элементы математической статистики Генеральная выборочная совокупность
- •Повторная и бесповторная выборка
- •Репрезентативная выборка
- •Статистическое распределение выборки
- •Методы построения точечных оценок
- •Билет №1 10
- •Билет №2
- •Билет №3
- •Билет №4
- •Билет № 5
- •Билет 6.
- •Билет 7
- •Билет 8
- •Билет 9.
- •Билет 10.
- •Билет 11.
- •Билет 12.
- •Билет № 13
- •Билет 14.
- •Билет 15. 16
- •Билет 16.
- •Билет 17.
- •Билет 18.
- •Билет 19.
- •Билет 20. 18
- •Билет 27.
- •Билет 28.
- •1.Теория вероятности
- •3 Т. «Сложения вероятности несовместных событий 20
- •5Формула полной вероятности
- •6.Вероятность наступления хотя бы 1-го события
- •10Вероятность отклонения относительной частоты от постоянной вероятности
- •11Случайная величина
- •12Интегральная ф-ия распределения
- •13Дифференциальная ф-ия распределения вероятностей св (её плотность)
- •14Числовые хар-ки св
- •15Дисперсия св (дискретной)
- •16Среднеквадратическое отклонение св х –
- •17Моменты св х:
- •18Важнейшие з-ны распределения вероятностей cв:
- •21Т.Чебышева
- •22Т. Ляпунова
- •26Вероятность попадания случайной точки в полосу
- •29Числовые хар-ки 2-мерной св (с-мы св):
- •31Нормальное распределение с-мы 2-х св
8.Числовые хар-ки случайной величины. 4
Математическое ожидание:
На практике часто полное описание случайной величины не слишком важно, достаточно знать нек. параметры. Их называют числовыми характеристиками. Наиболее важная – мат. ожидание или её среднее значение (М(Х))
xi |
X1 – Xn |
pi |
P1 - Pn |
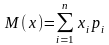
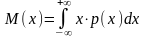
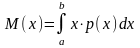
Дисперсия случайной величины:
Дисперсия характ. Разброс значений СВ около своего среднего значения (показатель рассеивания)
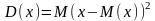
Дисперсия – мат. ожидание от квадрата отклонения СВ от своего мат. ожидания
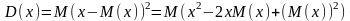
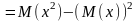 ;где
;где
Среднее
квадратичное отклонение:
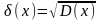
Пример: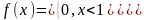
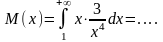
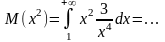 и
т.д.
и
т.д.
9.Биномиальный закон распределения.
Говорят, что СВ распределена по биномиальному закону, если она принимает значения 0, 1, 2, …, m, …,n а соответствующие вероятности вычисляются по формуле Бернулли:
0 - Pn(0), 1 – Pn(1), m – Pn(m), n – Pn(n)
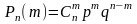 ;
;
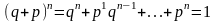 ;
;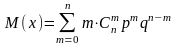 ;
;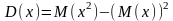
 ;
;
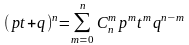 ;
;
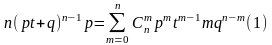
В (1) положим t=1
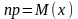 ;
;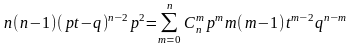 ;
;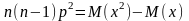 ;
;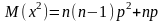 ;
;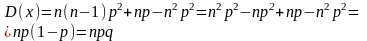
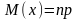 ;
;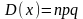
10.Распределение Пуассона. Равномерное распределение.
СВ распределена по закону Пуассона, если она принимает значения 0, 1, 2, 3,…, m,…,n, а соответсвующие вероятности по формуле Бернулли.
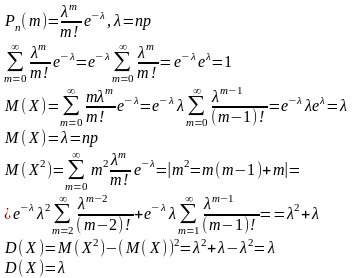

Равномерное распределение. 5
Непрерывная СВ распределена равномерно, если её плотность распределения вероятности имеет вид:
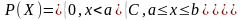
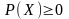
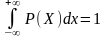
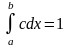
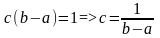
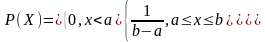
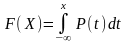 ;
; 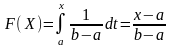
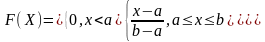
11. Показательное или экспоненциальное распределение.
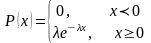

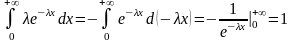
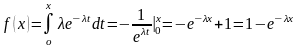
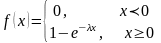

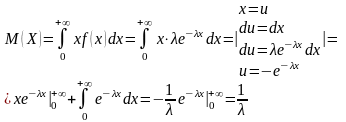
12. Нормальный закон распределения. Числовые 6 характеристики.
Непрерывная
случ. величина распред. по нормальному
з-ну, если плотность распределения
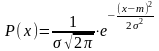 или
или
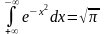

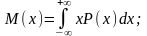
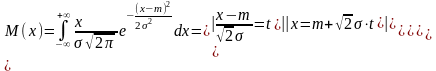
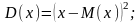
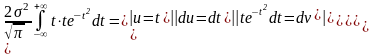
13. Ф-ция Лапласа и ее связь с интегр. ф-цией нормального распределения.
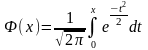 (1)
(1)
Осн. св-ва ф-ции Лапласа.
Т. к.
 —
непрерывна, то интеграл (1) существует
при любых х;
—
непрерывна, то интеграл (1) существует
при любых х;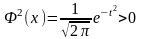 ,
то Ф(х) явл. Возрастающей;
,
то Ф(х) явл. Возрастающей;Функция Ф(х) — нечетная;
Ф(0)=0.
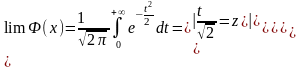
 ½
½
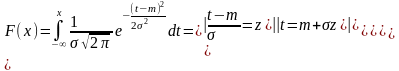

Вероятность
попадания в интервал длиной в
 ест
7 практически достоверное событие.
ест
7 практически достоверное событие.
14.Многомерные случайные величины(св)
Р ассмотрим
двумерную СВ. Законом распределения
наз-я соотношение, связывающее значение,
которое принимает СВ с соответствующими
вероятностями.
ассмотрим
двумерную СВ. Законом распределения
наз-я соотношение, связывающее значение,
которое принимает СВ с соответствующими
вероятностями.
x x1 x2………….xn
y
y1 P11 P12 ……P1N
y2 P21 P22 ……P2N
ym Pm1 Pm2 ……Pmn
x x1 x2……….. ……xn
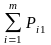
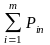
y y1 y2……….. ……ym
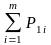
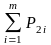
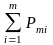
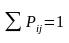 ; i=1…n;
j=1..m.
; i=1…n;
j=1..m.
Интегральная ф-ия распределения СВ.
F(x,y)=P(X<x,Y<y);
F(x1,x2,….,xn)=P(X1<x1,X2<x2,…,Xn<xn);
Основные св-ва интегральной ф-ии:
1. Значение ф-ии 0<F(x,y)<=1;
2.Функция неубывающая по любому из элементов;
3. Предельное соотношение
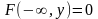 ;
;
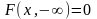 ;
;
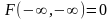 ;
;
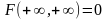 .
.
Дифференциальная ф-ия распределения СВ.
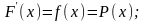
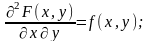
P(x<X<x+∆x,
y<Y<y+∆y)=F(x+∆x,
y+∆y)-F(x,
y+∆y)-(F(x+∆x,y)-F(x,y))=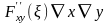
Основные св-ва :
1.
F(x,y)=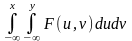 ;
;
2.Условие
нормировки
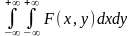
3. Диффер. Ф-ия неотрицательна f(x,y)>=0
Числовые характеристики ДСВ.
Корреляционный
момент двумерной СВ

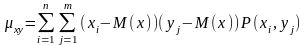
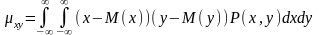
Теорема: корреляционный момент 2-ух независимых СВ x и y равен 0.
Док-во:
если независимы x,y
, то независимы x-M(x)
и y-M(y).
По св-ву мат. ожидания
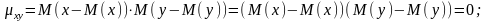 Коэффициент
корреляции:
Коэффициент
корреляции:
 .
.
