
- •Вопросы для подготовки к зачёту 21.06.2012 г. По дисциплине «Теория вероятностей и математическая статистика» (гр.Соэ 111 - 2012 год) Теоретическая часть
- •Виды случайных событий: зависимые и независимые, достоверные и невозможные, равновозможные, противоположные – их примеры.
- •Понятие комбинаторики, её основные определения и формулы, примеры основных понятий комбинаторики. Правила суммы и произведения комбинаторики.
- •Теорема умножения для двух зависимых событий, её условия и доказательство, следствие данной теоремы для нескольких событий, примеры применения данной теоремы и её следствия.
- •Теорема о формуле полной вероятности: её условие применения, словесная формулировка, математическая запись, её доказательство.
- •Понятие гипотез. Постановка задачи и вывод формул Бейеса. Что позволяют формулы Бейса?
- •Постановка задачи на ввод и вывод формулы Бернулли. Необходимые условия для применения формулы Бернулли.
- •Локальная теорема Лапласа: условия её применения, математическая запись теоремы, математическая формула и основное свойство функции используемой в этой теореме.
- •Интегральная теорема Лапласа: условия её применения, словесная формулировка, математическая запись теоремы, вывод формулы с использованием функции Лапласа, основные два свойства функции Лапласа.
- •Понятие случайной величины (св), правила обозначения св и возможных значений св. Понятие дискретной и непрерывной св, их примеры.
- •Понятие закона распределения дискретной случайной величины (дсв), способы задания закона дсв и их особенности, примеры способов задания законов дсв.
- •Распределение Пуассона для дискретной случайной величины (дсв): постановка задачи, условия применения, вывод аналитического выражения.
- •Геометрическое распределение дискретной случайной величины (дсв): постановка задачи, условия применения, вывод аналитического выражения, причина данного названия распределения.
- •Математическое ожидание (мож) числа появления события в одном испытании – словесная формулировка, доказательство. Вероятностный смысл мож – словесная формулировка, доказательство, два замечания.
- •Третье свойство мож (мож произведения 2-х независимых случ.Величин) – словесная формулировка, мат.Запись, доказательство, следствие.
- •Четвёртое свойство мож (мож суммы 2-х случ.Величин) - словесная формулировка, мат.Запись, доказательство, следствие.
- •Теорема о мож биномиального закона распределения – условия её применения, словесная формулировка, математическая запись, доказательство, замечание.
- •Необходимость введения и понятие ско случайных величин. Теорема о ско суммы взаимно независимых случайных величин (словесная формулировка, мат.Запись, доказательство).
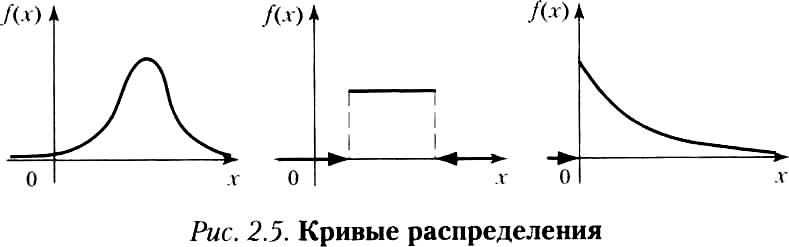
- •Плотность распределения случайной величины: определение, мат.Запись, 2 свойства (словесная формулировка, математическая запись, доказательство). Примеры кривых распределения случайных величин.
Плотность распределения случайной величины: определение, мат.Запись, 2 свойства (словесная формулировка, математическая запись, доказательство). Примеры кривых распределения случайных величин.
Непрерывную
случайную величину можно также
задать, используя другую функцию, которую
называют плотностью распределения или
плотностью вероятности (иногда ее
называют дифференциальной функцией).
.Плотностью
распределения
вероятностей непрерывной случайной
величины Х
называют
функцию
![]() - первую производную от функции
распределения
- первую производную от функции
распределения
![]() :
:![]() Т.е.
функция распределения является
первообразной для плотности распределения,
для описания распределения вероятностей
дсв плотность распределения
неприменима. Свойства плотности
распределения. Свойство 1.
Плотность
распределения—неотрицательная
функция:
Т.е.
функция распределения является
первообразной для плотности распределения,
для описания распределения вероятностей
дсв плотность распределения
неприменима. Свойства плотности
распределения. Свойство 1.
Плотность
распределения—неотрицательная
функция:
![]()
![]() Доказательство.
Функция распределения — неубывающая
функция, следовательно, ее производная
Доказательство.
Функция распределения — неубывающая
функция, следовательно, ее производная
 функция
неотрицательная. Геометрически (что
точки, принадлежащие графику
плотности распределения, расположены
либо над осью Ох,
либо на этой оси) График плотности
распределения
называют кривой
распределения.
функция
неотрицательная. Геометрически (что
точки, принадлежащие графику
плотности распределения, расположены
либо над осью Ох,
либо на этой оси) График плотности
распределения
называют кривой
распределения.
Рис.1. Примеры кривых распределения (нормального, равномерного и экспоненциального законов распределения)
Свойство 2. Несобственный интеграл от плотности распределения в пределах от - ∞ до + ∞ равен единице:
![]()
Д![]() оказательство.Несобственный интеграл
выражает вероятность события, состоящего
в том, что случайная величина примет
значение, принадлежащее интервалу (
оказательство.Несобственный интеграл
выражает вероятность события, состоящего
в том, что случайная величина примет
значение, принадлежащее интервалу (![]() ).
Очевидно, такое событие достоверно,
следовательно, вероятность его равна
единице. Геометрически это означает,
что вся площадь криволинейной
трапеции, ограниченной осью Ох
и кривой распределения, равна единице.
В частности, если все возможные значения
случайной величины принадлежат интервалу
(а,
b),
то
).
Очевидно, такое событие достоверно,
следовательно, вероятность его равна
единице. Геометрически это означает,
что вся площадь криволинейной
трапеции, ограниченной осью Ох
и кривой распределения, равна единице.
В частности, если все возможные значения
случайной величины принадлежат интервалу
(а,
b),
то![]() Пример. Плотность распределения
случайной величины Х
задана:
Пример. Плотность распределения
случайной величины Х
задана:
Н![]() айти
постоянный параметр а.
айти
постоянный параметр а.
Решение. Плотность распределения должна удовлетворять условию
Поэтому
потребуем, чтобы выполнялось равенство
![]() Отсюда
Отсюда
![]()
Найдем
неопределенный интеграл:![]() Вычислим
несобственный интеграл:
Вычислим
несобственный интеграл:
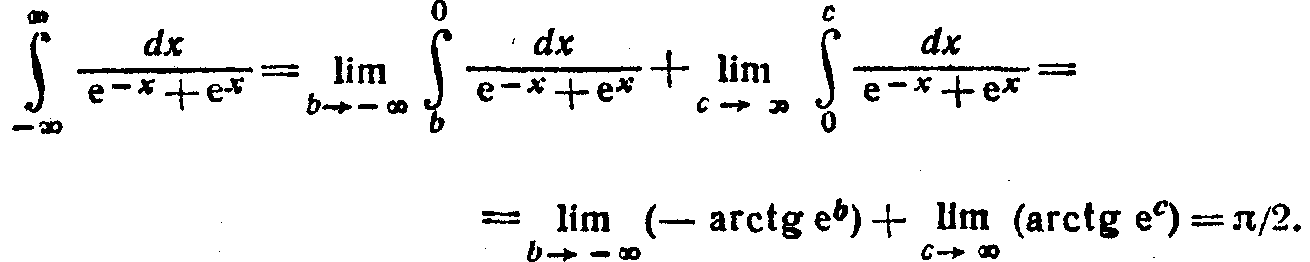 Таким образом, искомый параметр
Таким образом, искомый параметр
![]()
Взаимосвязь функции и плотности распределения (математическая запись, доказательство), вероятностный смысл плотности распределения (словесная формулировка, доказательство, геометрическое пояснение).
Зная плотность распределения f (x), можно найти функцию распределения F (x) по формуле
![]() Действительно,
мы обозначили через F
(x)
вероятность того, что случайная величина
примет значение, меньшее x.
т. е.
Действительно,
мы обозначили через F
(x)
вероятность того, что случайная величина
примет значение, меньшее x.
т. е.![]()
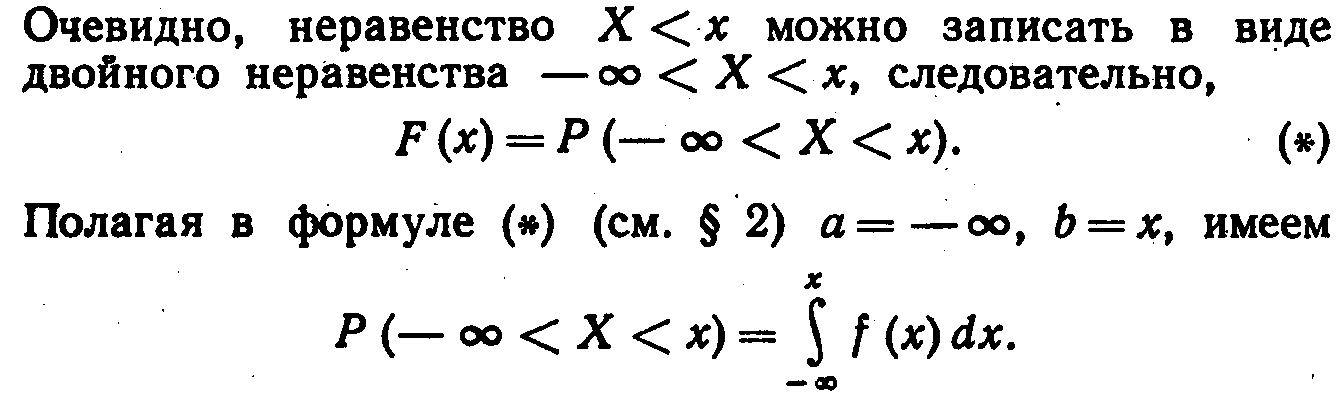
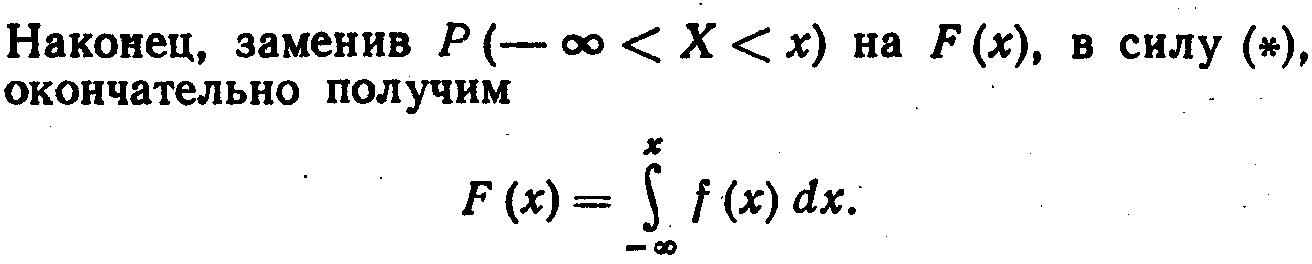
Т![]() аким
образом, зная плотность распределения,
можно найти функцию распределения.
Разумеется, по известной функции
распределения может быть найдена
плотность распределения, а именно:
аким
образом, зная плотность распределения,
можно найти функцию распределения.
Разумеется, по известной функции
распределения может быть найдена
плотность распределения, а именно:
Пример. Найти функцию распределения по данной плотности распределения:
![]() Построить
график найденной функции.
Построить
график найденной функции.
![]()
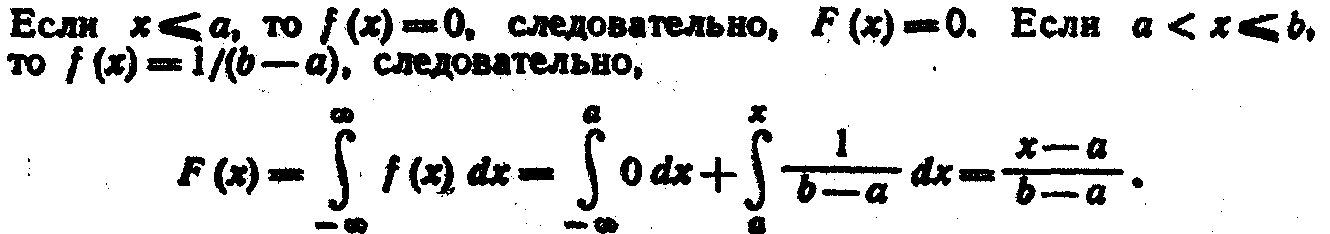
![]()
И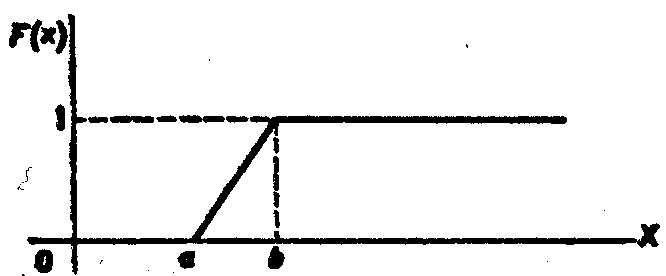 так,
искомая функция распределения
так,
искомая функция распределения
![]()
