
- •Вопросы для подготовки к зачёту 21.06.2012 г. По дисциплине «Теория вероятностей и математическая статистика» (гр.Соэ 111 - 2012 год) Теоретическая часть
- •Виды случайных событий: зависимые и независимые, достоверные и невозможные, равновозможные, противоположные – их примеры.
- •Понятие комбинаторики, её основные определения и формулы, примеры основных понятий комбинаторики. Правила суммы и произведения комбинаторики.
- •Теорема умножения для двух зависимых событий, её условия и доказательство, следствие данной теоремы для нескольких событий, примеры применения данной теоремы и её следствия.
- •Теорема о формуле полной вероятности: её условие применения, словесная формулировка, математическая запись, её доказательство.
- •Понятие гипотез. Постановка задачи и вывод формул Бейеса. Что позволяют формулы Бейса?
- •Постановка задачи на ввод и вывод формулы Бернулли. Необходимые условия для применения формулы Бернулли.
- •Локальная теорема Лапласа: условия её применения, математическая запись теоремы, математическая формула и основное свойство функции используемой в этой теореме.
- •Интегральная теорема Лапласа: условия её применения, словесная формулировка, математическая запись теоремы, вывод формулы с использованием функции Лапласа, основные два свойства функции Лапласа.
- •Понятие случайной величины (св), правила обозначения св и возможных значений св. Понятие дискретной и непрерывной св, их примеры.
- •Понятие закона распределения дискретной случайной величины (дсв), способы задания закона дсв и их особенности, примеры способов задания законов дсв.
- •Распределение Пуассона для дискретной случайной величины (дсв): постановка задачи, условия применения, вывод аналитического выражения.
- •Геометрическое распределение дискретной случайной величины (дсв): постановка задачи, условия применения, вывод аналитического выражения, причина данного названия распределения.
- •Математическое ожидание (мож) числа появления события в одном испытании – словесная формулировка, доказательство. Вероятностный смысл мож – словесная формулировка, доказательство, два замечания.
- •Третье свойство мож (мож произведения 2-х независимых случ.Величин) – словесная формулировка, мат.Запись, доказательство, следствие.
- •Четвёртое свойство мож (мож суммы 2-х случ.Величин) - словесная формулировка, мат.Запись, доказательство, следствие.
- •Теорема о мож биномиального закона распределения – условия её применения, словесная формулировка, математическая запись, доказательство, замечание.
- •Необходимость введения и понятие ско случайных величин. Теорема о ско суммы взаимно независимых случайных величин (словесная формулировка, мат.Запись, доказательство).
- •Плотность распределения случайной величины: определение, мат.Запись, 2 свойства (словесная формулировка, математическая запись, доказательство). Примеры кривых распределения случайных величин.
Третье свойство мож (мож произведения 2-х независимых случ.Величин) – словесная формулировка, мат.Запись, доказательство, следствие.
Мож
произведения двух независимых
случайных величин
равно
произведению их математических
ожиданий:![]() Доказательство.
Пусть
независимые св Х и У заданы законами
распределения вероятн:
Доказательство.
Пусть
независимые св Х и У заданы законами
распределения вероятн:
![]()
Составим все значения, которые может принимать случайная величина XY. Для этого перемножим все возможные значения Х на каждое возможное значение У. В итоге получим: x1y1, x2y1, x1y2 и x2y2.
Учитывая замечание 3 ( P(xiyi)= P(xi) P(yi) ), напишем закон распределения XY, предполагая для простоты, что все возможные значения произведения различны (если это не так, то доказательство проводится аналогично):
![]()
Математическое ожидание ( согласно определения МОЖ) равно сумме произведений всех возможных значений ДСВ на их соответствующие вероятности:
![]()
или
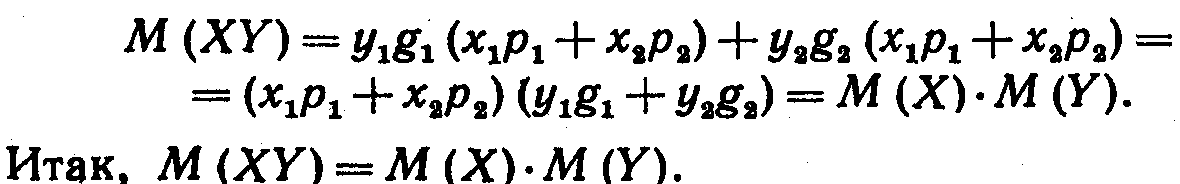
Следствие. Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению их математических ожиданий.
Например, для трех случайных величин имеем:
![]()
Для произвольного числа случайных величин доказательство проводится методом математической индукции.
Пример 1. Независимые случайные величины Х и У заданы следующими законами распределения:
![]()
Найти математическое ожидание случайной величины XY.
Решение. Найдем математические ожидания каждой из данных величин:
![]()
Для упрощения выкладок мы ограничились малым числом возможных значений. В общем случае (большим числом возможных значений) доказательство аналогичное.
Случайные величины Х и У независимые, поэтому искомое математическое ожидание
![]()
Замечание 4. Определим сумму случайных величин X и Y как случайную величину X+Y, возможные значения которой равны суммам каждого возможного значения Х с каждым возможным значением У;
Вероятности возможных значений X+Y для независимых величин Х и У равны произведениям вероятностей слагаемых, а для зависимых величин — произведениям вероятности одного слагаемого на условную вероятность второго.
Заметим, что некоторые суммы х + у могут оказаться равными между собой. В этом случае вероятность возможного значения суммы равна сумме соответствующих вероятностей.
Например, если х1 + у2= х3 + у5 и вероятности этих возможных значений соответственно равны P(х1 + у2)= p12 и P(х3 + у5 )=p35, то вероятность х1 + у2 (или, что тоже, х3 + у5) равна P(х1 + у2)= p12+ p35.
Следующее ниже свойство справедливо как для независимых, так и для зависимых случайных величин.
Четвёртое свойство мож (мож суммы 2-х случ.Величин) - словесная формулировка, мат.Запись, доказательство, следствие.
Свойство
4. Математическое
ожидание суммы двух случайных величин
равно сумме математических ожиданий
слагаемых:![]() Доказательство.
Пусть св Х
и Y
заданы законами распределения:
Доказательство.
Пусть св Х
и Y
заданы законами распределения:
![]() Составим
все возможные значения величины X+Y.
получим-
x1
+ y1,
x1
+ y2,
x2
+ y1,
x2
+ y2.
Предположим для простоты, что эти
возможные значения различны ,обозначим
их вероятности Мож величины Х + Y
равно сумме произведений возможных
значений этой величины на соответствующие
их вероятности:
Составим
все возможные значения величины X+Y.
получим-
x1
+ y1,
x1
+ y2,
x2
+ y1,
x2
+ y2.
Предположим для простоты, что эти
возможные значения различны ,обозначим
их вероятности Мож величины Х + Y
равно сумме произведений возможных
значений этой величины на соответствующие
их вероятности:
![]()
![]() или
или
В общем
случае доказательство аналогичное.
Докажем, что p11+p12=p1.
x1
(вероятность этого события равна p1),
влечёт за собой событие X+Y
примет значение x1+y1
или
x1+y2
(вероятность этого события по теореме
сложения равна p11+p12)
и
обратно.
Отсюда
и следует, что p11+p12=p1
.
Аналогично доказываются равенства:
p21+p22=p2;
p11+p21=g1;
p12+p22=g2;
Подставляя правые части этих равенств
в соотношение (*), получим
![]() или окончательно
или окончательно
![]() Следствие.
Математическое
ожидание суммы нескольких случайных
величин равно сумме математических
ожиданий слагаемых. Пример. Производится
3 выстрела с вероятностями попадания в
цель, равными р1==0,4;
p2==0,3
и р3=0,6.
Найти математическое ожидание общего
числа попаданий.
Следствие.
Математическое
ожидание суммы нескольких случайных
величин равно сумме математических
ожиданий слагаемых. Пример. Производится
3 выстрела с вероятностями попадания в
цель, равными р1==0,4;
p2==0,3
и р3=0,6.
Найти математическое ожидание общего
числа попаданий.
