
- •1. Предмет теории вероятностей. Случайный эксперимент.
- •2. Классическое определение вероятности.
- •3. Геометрическое определение вероятности
- •4. Аксиоматическое определение вероятности
- •5. Условные вероятности
- •6. Независимые события
- •7. Формулы полной вероятности и Байеса
- •8. Схема независимых испытаний Бернулли
- •9. Случайные величины. Функция распределения случайной величины и ее свойства
- •10. Дискретные случайные величины. Закон распределения дсв.
- •12. Непрерывные случайные величины. Плотность вероятностей
- •13. Важнейшие непрерывные случайные величины
- •1 4. Математическое ожидание св.
- •15. Моменты. Дисперсия. Среднее квадратическое отклонение.
- •16. Чх дискретных и непрерывных случайных величин
- •17. Случайные векторы. Фр случайного вектора и ее свойства.
- •18. Дискретные случайные векторы. Зр дискретного случайного вектора
- •19. Непрерывные случайные векторы. Плотность вероятностей и ее свойства
- •20. Пример. (Равномерное распределение в области ).
- •21. Независимость случайных величин
- •22. Условные законы распределения и условные числовые характеристики
- •23. Числовые характеристики случайных векторов
- •24. Теоремы о числовых характеристиках
- •25. Некоррелированность случайных величин и ее связь с независимостью
- •26. Коэффициент корреляции его свойства
- •27. Многомерное нормальное (гауссовское) распределение
- •28. Функции случайных аргументов
- •29. Композиция (свертка) законов распределения
- •30. Неравенство Чебышева
- •31. Законы больших чисел
- •32. Теорема 3 (збч для независимых, одинаково распределенных св).
- •33. Центральная предельная теорема
- •34. Теорема 2 (Ляпунова) (цпт для независимых, разнораспределенных св)
8. Схема независимых испытаний Бернулли
Предположим, что некоторый эксперимент может повторяться при неизменных условиях сколько угодно раз, и эти повторения не зависят друг от друга. В этом случае говорят о проведении последовательности независимых испытаний. События являются независимыми в совокупности.
Простейшей является последовательность независимых испытаний, в каждом из которых возможно только 2 исхода: успех – У (1) и неуспех – Н (0). Последовательность независимых испытаний с двумя исходами называется схемой независимых испытаний Бернулли.
Обозначим вероятность успеха
![]() ,
а вероятность неуспеха
,
а вероятность неуспеха
![]() .
.
При проведении n
независимых испытаний по схеме Бернулли
пространство элементарных событий
имеет вид:
![]() ,
,
а вероятности элементарных событий в силу независимости испытаний вычисляются по формуле:
![]() ,
то есть -.
,
то есть -.![]()
В связи с рассмотрением схемы независимых
испытаний Бернулли обычно представляют
интерес события
![]() ={В
n испытаниях наступило
ровно m успехов}= =
={В
n испытаниях наступило
ровно m успехов}= =![]() .
.
Обозначим вероятность
![]() и вычислим ее. Поскольку для любого
и вычислим ее. Поскольку для любого
![]() вероятность
вероятность
![]() ,
а общее количество исходов, содержащихся
в
,
равно числу способов размещения m
единиц в последовательности длины n
из нулей и единиц, то
,
а общее количество исходов, содержащихся
в
,
равно числу способов размещения m
единиц в последовательности длины n
из нулей и единиц, то
![]() .
Таким образом,
.
Таким образом,
![]() .
.
Полученная формула называется формулой Бернулли. Она даёт выражение для вероятности наступления m успехов в n независимых испытаниях по схеме Бернулли с неизменной вероятностью успеха в одном испытании равной p и с вероятностью неуспеха равной q = 1 – p.
Поскольку события
![]() образуют полную группу событий, то
образуют полную группу событий, то
![]() .
Тот же результат можно получить и на
основании бинома Ньютона:
.
Тот же результат можно получить и на
основании бинома Ньютона:
![]()
Исследуем поведение вероятностей
![]() в зависимости от m.
Для этого вычислим отношение:
в зависимости от m.
Для этого вычислим отношение:
![]() .
.
Отсюда следует, что вероятности
возрастают, когда
![]() или, что эквивалентно,
или, что эквивалентно,
![]() .
.
Вероятности
убывают, когда
![]() или, что эквивалентно,
или, что эквивалентно,
![]() .
.
И, наконец,
![]() ,
если
,
если
![]() .
.
Определение. Число успехов m = m0, при котором вероятности достигают максимума, называются наивероятнейшим числом успехов.
Из проведённых рассуждений следует,
что наивероятнейшее число успехов m0
определяется из двойного неравенства:
![]() .
При этом:
.
При этом:
Если число
 нецелое, то существует одно наивероятнейшее
число успехов:
нецелое, то существует одно наивероятнейшее
число успехов:
 .
.Если число целое, то существует два наивероятнейших числа успехов:
 и
и
 .
.Если число
 целое, то
целое, то
 .
.
Вычисления по формуле Бернулли при больших m и n весьма трудоёмкие. На практике в этом случае используют асимптотические приближения для вероятностей , основанные на предельных теоремах Пуассона и Муавра-Лапласа.
9. Случайные величины. Функция распределения случайной величины и ее свойства
Случайная величина (СВ) – это числовая функция, значения которой заранее (до наблюдения) нельзя точно определить, то есть функция, зависящая от случайного исхода и принимающая свои значения с некоторыми вероятностями. Примеры СВ:
а) число пассажиров в автобусе (конечное число значений);
б) число вызовов на телефонной станции за время Т (счетное число значений);
в) время безотказной работы прибора за время Т (несчетное число значений).
Обозначают СВ прописными буквами латинского алфавита X, Y, Z,…, а их значения соответствующими строчными буквами x, y, z,….
Формальное определение СВ.
Определение. Случайной величиной
![]() называется функция X
= X(ω), определенная
на пространстве элементарных событий
и принимающая действительные значения
(
называется функция X
= X(ω), определенная
на пространстве элементарных событий
и принимающая действительные значения
(![]() ).
).
Для того, чтобы определять вероятности событий, связанных со СВ, и делать это одним и тем же способом для любых СВ, в теории вероятностей вводится понятие функции распределения.
Определение. Функцией распределения
СВ
называется функция
![]() действительной переменной
действительной переменной
![]() ,
определяемая при каждом х равенством:
,
определяемая при каждом х равенством:
![]() .
.
Геометрически функция распределения
(ФР) означает вероятность попадания СВ
левее заданной точки
:
Свойства ФР.
1.
![]() для любого
для любого
![]() (свойство очевидно, так как
(свойство очевидно, так как
![]() - вероятность).
- вероятность).
2. ФР является функцией неубывающей:
![]() .
.
▲
![]() .
Поэтому в силу свойства 6 вероятности
.
Поэтому в силу свойства 6 вероятности
![]() ■.
■.
3.
![]() .
.
![]() в силу свойства 5 вероятности.
в силу свойства 5 вероятности.
![]() в силу аксиомы нормированности ■.
в силу аксиомы нормированности ■.
4. ФР является функцией непрерывной
слева, то есть для любого
![]() ,
,
где
![]() - предел слева ФР в точке х.
- предел слева ФР в точке х.
5. Для любого
![]() ,
где
,
где
![]() - предел справа ФР в точке х.
- предел справа ФР в точке х.
З амечание.
Геометрически свойства 4 и 5 означают
следующее. В точках
,
где ФР имеет разрыв 1 рода, то есть когда
амечание.
Геометрически свойства 4 и 5 означают
следующее. В точках
,
где ФР имеет разрыв 1 рода, то есть когда
![]() ,
значением ФР является левое (нижнее,
меньшее). В точках непрерывности ФР
свойства 4 и 5 содержательными не являются.
,
значением ФР является левое (нижнее,
меньшее). В точках непрерывности ФР
свойства 4 и 5 содержательными не являются.
6. Вероятность попадания СВ
в интервал
![]() определяется как приращение ФР на этом
интервале: для любых
определяется как приращение ФР на этом
интервале: для любых
![]()
![]() .
.
▲ Поскольку событие
![]() и слагаемые в сумме являются несовместными,
то в силу аддитивности вероятности
и слагаемые в сумме являются несовместными,
то в силу аддитивности вероятности
![]() или
или
![]() ■.
■.
7. Для любого
![]() ,
где
,
где
![]() - величина скачка ФР в точке
.
- величина скачка ФР в точке
.
▲ Поскольку событие
![]() и слагаемые в сумме являются несовместными,
то в силу аддитивности вероятности
и слагаемые в сумме являются несовместными,
то в силу аддитивности вероятности
![]() ,
,
а с учетом свойства 5 ФР
![]() ■.
■.
С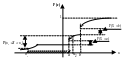 ледствие.
Если ФР непрерывна в точке
,
то
ледствие.
Если ФР непрерывна в точке
,
то
![]() .
Если ФР непрерывна для любого
,
то
для любого
.
.
Если ФР непрерывна для любого
,
то
для любого
.
8.
![]() .
9.
.
9.
![]() .
.
10.
![]() .
.
В общем случае график ФР может иметь вид:
В приложениях, как правило, встречаются СВ, ФР которых являются либо везде кусочно-постоянными (дискретные СВ), либо везде непрерывными и даже гладкими (непрерывные СВ). В каждом из этих случаев существуют более удобные, чем ФР, вероятностные характеристики СВ.
