
- •1. Предмет теории вероятностей. Случайный эксперимент.
- •2. Классическое определение вероятности.
- •3. Геометрическое определение вероятности
- •4. Аксиоматическое определение вероятности
- •5. Условные вероятности
- •6. Независимые события
- •7. Формулы полной вероятности и Байеса
- •8. Схема независимых испытаний Бернулли
- •9. Случайные величины. Функция распределения случайной величины и ее свойства
- •10. Дискретные случайные величины. Закон распределения дсв.
- •12. Непрерывные случайные величины. Плотность вероятностей
- •13. Важнейшие непрерывные случайные величины
- •1 4. Математическое ожидание св.
- •15. Моменты. Дисперсия. Среднее квадратическое отклонение.
- •16. Чх дискретных и непрерывных случайных величин
- •17. Случайные векторы. Фр случайного вектора и ее свойства.
- •18. Дискретные случайные векторы. Зр дискретного случайного вектора
- •19. Непрерывные случайные векторы. Плотность вероятностей и ее свойства
- •20. Пример. (Равномерное распределение в области ).
- •21. Независимость случайных величин
- •22. Условные законы распределения и условные числовые характеристики
- •23. Числовые характеристики случайных векторов
- •24. Теоремы о числовых характеристиках
- •25. Некоррелированность случайных величин и ее связь с независимостью
- •26. Коэффициент корреляции его свойства
- •27. Многомерное нормальное (гауссовское) распределение
- •28. Функции случайных аргументов
- •29. Композиция (свертка) законов распределения
- •30. Неравенство Чебышева
- •31. Законы больших чисел
- •32. Теорема 3 (збч для независимых, одинаково распределенных св).
- •33. Центральная предельная теорема
- •34. Теорема 2 (Ляпунова) (цпт для независимых, разнораспределенных св)
20. Пример. (Равномерное распределение в области ).
Говорят, что
имеет равномерное распределение в
области
,
если его ПВ постоянна внутри области
![]() :
:
![]()
Константа С при этом однозначно определяется из условия нормировки:
![]() ,
то есть
,
то есть
![]() ,
где
,
где
![]() - площадь области
.
- площадь области
.
а) Равномерное распределение в прямоугольнике.
Н епрерывный
случайный вектор
имеет равномерное распределение в
прямоугольнике
епрерывный
случайный вектор
имеет равномерное распределение в
прямоугольнике
![]() со сторонами, параллельными осям
координат, если его плотность вероятностей
имеет вид:
со сторонами, параллельными осям
координат, если его плотность вероятностей
имеет вид:
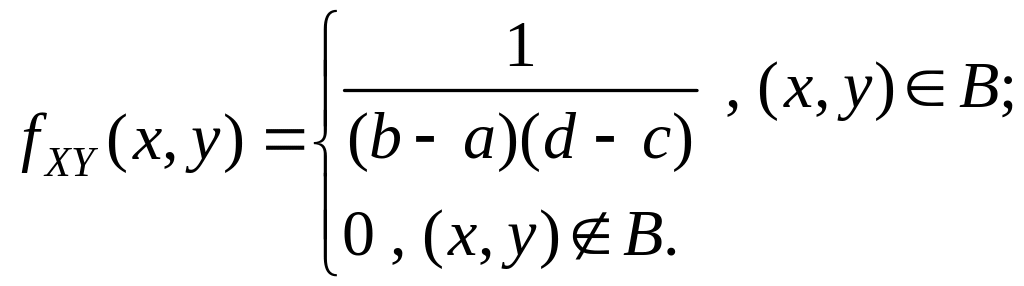
Найдем одномерные ПВ координат .
В соответствии со свойством 4 двумерной
ПВ
![]() .
.
Таким образом,
 то есть
.
то есть
.
Аналогично,
![]() .
.
Таким образом,
 то есть
то есть
![]() .
.
б) Равномерное распределение в круге.
Н епрерывный
случайный вектор
имеет равномерное распределение в круге
епрерывный
случайный вектор
имеет равномерное распределение в круге
![]() ,
если его плотность вероятностей имеет
вид:
,
если его плотность вероятностей имеет
вид:

Найдем одномерные ПВ координат .
В соответствии со свойством 4 двумерной ПВ
 .
.
Таким образом,

Аналогично .
.
Таким образом,

21. Независимость случайных величин
Известно, что события А и В являются независимыми, если . Аналогично определяется и независимость СВ и , только вместо событий А и В следует использовать события, связанные с этими СВ.
Определение. СВ
и
называются независимыми, если для
любых
![]() имеет место равенство:
имеет место равенство:
![]() или,
или,
![]() .
(3.9)
.
(3.9)
Если при каких-либо равенство (3.9) не выполняется, то СВ и являются зависимыми.
Таким образом, независимость СВ означает, что их совместная ФР равна произведению одномерных ФР и , или, как еще говорят, двумерная ФР факторизуется.
Установим условия независимости СВ в дискретном и непрерывном случаях.
Лемма 1. Пусть
-ДСВ, принимающий значения
с вероятностями
,
;
![]() ,
- вероятности
,
,
- вероятности
,
![]() - вероятности
.
- вероятности
.
ДСВ
и
являются независимыми тогда и только
тогда, когда при всех
и
![]() ,
(3.10)
,
(3.10)
то есть вероятность факторизуется.(опр-е незав-ти дсв)
Если при каких-либо и равенство (3.10) не выполняется, то ДСВ и являются зависимыми.
Н еобходимость.
Пусть дискретные случайные величины
и
являются независимыми. Тогда
для любых
.
еобходимость.
Пусть дискретные случайные величины
и
являются независимыми. Тогда
для любых
.
Обозначим
![]() прямоугольник со сторонами, параллельными
осям координат, который содержит точку
и не содержит других значений ДСВ
.
прямоугольник со сторонами, параллельными
осям координат, который содержит точку
и не содержит других значений ДСВ
.
Тогда
![]() (по построению
)
=
(по построению
)
=
=
![]() (по свойству 4) =
(по свойству 4) =
=
![]() (в силу независимости случайных величин)
=
(в силу независимости случайных величин)
=
![]() (по построению
),
(по построению
),
то есть , и так можно сделать для любого значения .
Достаточность. Если выполняется
равенство (3.10), то в соответствии с
определениями ФР
,
![]() имеем:
имеем:
![]()
![]() ,
то есть ДСВ
и
являются независимыми ■.
,
то есть ДСВ
и
являются независимыми ■.
Лемма 2. Пусть
-
,
- его ПВ,
и
![]() - одномерные ПВ его координат, определяемые
по формулам
(3.8).
- одномерные ПВ его координат, определяемые
по формулам
(3.8).
НСВ
и
являются независимыми ттт,к
![]() (3.11) (опр-е нез-ти нсв)
(3.11) (опр-е нез-ти нсв)
для всех , являющихся точками непрерывности функций и , то есть двумерная ПВ факторизуется.
▲ Необходимость. Если НСВ и являются независимыми, то .
Дифференцируя это равенство по
и по
,
получаем:
![]()
и, следовательно, в соответствии с определениями ПВ , и , справедливо равенство: в точках непрерывности функций и .
Достаточность. Проинтегрируем
равенство (3.11) по первому аргументу в
пределах от
![]() до
и по второму аргументу в пределах от
до
.
В результате получаем:
до
и по второму аргументу в пределах от
до
.
В результате получаем:
![]() .
и, следовательно, в соответствии с
определениями ФР
,
и
для любых
справедливо равенство:
,
.
и, следовательно, в соответствии с
определениями ФР
,
и
для любых
справедливо равенство:
,
то есть СВ и являются независимыми ■.
Леммы 1 и 2 показывают, что, если СВ и являются независимыми, то двумерный ЗР полностью определяется одномерными ЗР его координат (то есть понятие в этом случае вырождается).
Определение. СВ
называются независимыми в совокупности,
если для любого
![]() ,
для любого набора индексов
,
для любого набора индексов
![]() и для любых
и для любых
![]()
![]() или
или
![]() ,
,
где
![]() – ФР СВ
– ФР СВ
![]() ,
то есть многомерная ФР
,
то есть многомерная ФР
![]() факторизуется.
факторизуется.
Для независимости в совокупности
непрерывных случайных величин
![]() ,
имеющих плотности вероятностей
,
имеющих плотности вероятностей
![]() ,
,
![]() необходимо и достаточно, чтобы
необходимо и достаточно, чтобы
![]() ,
во всех точках непрерывности функций
и
,
во всех точках непрерывности функций
и
![]() ,
.
,
.
