1.9. Реализация метода наименьших квадратов в пакете matlab

Метод наименьших квадратов реализован в подавляющем большинстве современных математических и прикладных вычислительных пакетов программ. Например, в пакете математического программного обеспечения MATLAB при решении задачи идентификации методом МНК для линейной по параметрам полиномиальной модели используется функция polyfit:

Эта функция отыскивает коэффициенты полинома порядка m, доставляющие минимум критерия метода МНК, когда исходная выборка задана векторами u и х. Результирующий вектор p размерности m + 1 содержит оптимальные коэффициенты полинома в порядке убывания степеней его членов:

.

Функция polyval служит для пересчета полиномиальной модели с заданными коэффициентами:

Вектор x составлен из значений полиномиальной модели МНК с коэффициентами α, соответствующих вектору значений независимой переменной u.

Покажем применение метода МНК для задачи восстановления зависимости по выборке . Выборочные значения функции содержат нормально распределенную случайную ошибку со стандартным отклонением 0.1. Оператор поиска коэффициентов полиномиальной модели имеет вид

>> α = polyfit(1:10,(1:10) + normrnd(0,0.1,1,10),1)

α =

0.9931 0.0612

>>

Полином с найденными коэффициентами в выборочных точках рассчитывается следующим образом:

>> polyval(α,1:10)

ans =

Columns 1 through 10

1.0542 2.0473 3.0404 4.0335 5.0266 6.0196 7.0127 8.0058 8.9989 9.9919

>>

Приведенный пример наглядно иллюстрирует простоту программной реализации метода наименьших квадратов в пакете MATLAB.

1.10. Метод стохастической аппроксимации

Метод стохастической аппроксимации был разработан в 1951 г. для определения единственного корня уравнения в случае, когда значение этой функции измеряется с некоторой случайной ошибкой:

.

(1.66)

Алгоритмы, реализующие метод, получили название алгоритмов Робинса–Монро. Затем подобные алгоритмы были использованы для отыскания экстремума унимодальной функции , также включающей случайный шум согласно уравнению (1.66). Алгоритмы такого типа называют алгоритмами Кифера–Волфовитца. А. Дворецким была сформулирована и доказана теорема, которая дала наиболее слабые условия сходимости для любых типов алгоритмов стохастической аппроксимации. Пользуясь результатами этой теоремы, можно построить различные алгоритмы идентификации параметров модели.

Получим простейший алгоритм стохастической аппроксимации на примере решения задачи по отысканию оценки истинного значения величины X на основе ее n измерений: x_i, i = 1, 2, …, n. Пусть , где – некоторая случайная помеха с нулевым средним и конечной дисперсией: , . Из математической статистики известно, что наилучшей оценкой X будет среднее арифметическое ее n измерений:

.

(1.67)

Согласно закону больших чисел Колмогорова можно записать

.

(1.68)

Получим рекуррентную формулу для вычисления по среднему значению выборки после n измерений и поступившему новому измерению . По формуле (1.67) для n + 1 измерений имеем:

.

(1.69)

Подставляя выражение (1.67) в (1.69), получим:

.

(1.70)

Последнее равенство преобразуем к виду:

.

(1.71)

Это рекуррентное выражение и есть алгоритм стохастической аппроксимации для определения оценки параметра x по его зашумленным наблюдениям. При этом новая оценка равна сумме старой оценки и корректирующего члена с некоторым весовым коэффициентом . С ростом n эти весовые коэффициенты образуют убывающую последовательность

,

(1.72)

которая обладает еще двумя важнейшими асимптотическими свойствами:

,	(1.73)
.	(1.74)

Эти свойства можно объяснить следующим образом. Вес корректирующего члена, т. е. его влияние на оценку, будет уменьшаться в соответствии с условием (1.72), поскольку закон больших чисел гарантирует, что при этой процедуре оценка стремится к истинному значению параметра с увеличением числа итераций. Однако коррекция должна производиться вне зависимости от того, сколько итераций уже было сделано с начала процедуры оценивания, что и отражается условием (1.73), в котором сумма корректирующей последовательности расходится, значит эффект от корректирующего члена никогда не будет равен нулю. Свойство (1.74) является необходимым для сходимости общей процедуры стохастической аппроксимации, поскольку при большом числе итераций оно влечет за собой уменьшение влияния индивидуальных ошибок.

Кроме последовательности вида этим условиям удовлетворяют и многие другие последовательности, например , где q > 1/2. Таким образом, любой рекуррентный алгоритм вида (1.71) или в более общем случае вида , где последовательность весовых коэффициентов при корректирующем члене удовлетворяет условиям (1.72)–(1.74), согласно теореме Дворецкого является алгоритмом стохастической аппроксимации (типа Робинса–Монро) и обеспечивает сходимость оценок к истинным параметрам по вероятности.

В качестве примера рассмотрим алгоритм стохастической аппроксимации для оценивания параметров линейной регрессии. При этом последовательность весовых коэффициентов, удовлетворяющих условиям (1.72)–(1.74), выберем в виде ряда , где . Корректирующий член или невязку в общей рекуррентной формуле можно определить, используя скалярный квадратичный показатель качества идентификации:

,

(1.75)

откуда невязку можно получить, продифференцировав этот показатель по :

.

(1.76)

Окончательно имеем следующий рекуррентный алгоритм стохастической аппроксимации для оценивания параметров линейной регрессии:

.

(1.77)

Важным достоинством алгоритмов стохастической аппроксимации является то, что для их применения не требуется никаких специальных знаний о вероятностном распределении или каких-либо статистических характеристиках ошибки измерения. Исключение составляет информация о том, что ошибки измерения образуют последовательность независимых случайных величин с нулевым средним (для несмещенности оценок) и ограниченной дисперсией. Заметим, что на практике обеспечение этих условий обычно не вызывает затруднений. Кроме того, алгоритмы стохастической аппроксимации очень просты при вычислениях. Однако при этом они не обладают какими-либо оптимальными свойствами и непригодны для отыскания глобального экстремума многоэкстремальных функций, а также очень медленно сходятся к истинному значению параметра. Это связано с тем, что основное внимание в этих алгоритмах согласно теореме Дворецкого уделяется самому факту сходимости, а не скорости этой сходимости.

Эта проблема была разрешена во многих алгоритмах, ускоряющих процедуру сходимости по сравнению с обычным алгоритмом стохастической аппроксимации. Одним из наиболее удачных и эффективных является алгоритм, в котором коэффициенты остаются постоянными до тех пор, пока корректирующий член сохраняет свой знак, и только после изменения знака этого члена берется следующий элемент последовательности. Дж. Саридисом было доказано, что такая схема обеспечивает сходимость по вероятности и значительно ускоряет скорость сходимости.
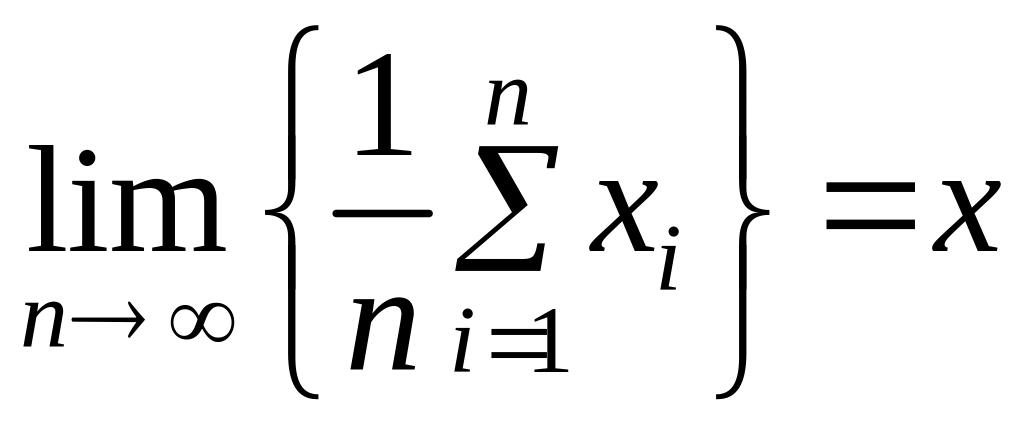