
- •Е. Д. Агафонов, о. В. Шестернёва Математическое моделирование линейных динамических систем
- •© Сибирский федеральный университет, 2011
- •Оглавление
- •Предисловие
- •Глава 1 Параметрические регрессионные модели
- •1.1. Линейная регрессия
- •1.2. Метод наименьших квадратов. Критерий метода наименьших квадратов
- •1.3. Идентификация линейных по параметрам моделей с использованием метода наименьших квадратов
- •1.4. Линейный метод наименьших квадратов с использованием ортогональных полиномов
- •1.5. Рекуррентный метод наименьших квадратов
- •1.6. Линейная аппроксимация метода наименьших квадратов
- •1.7. Методы максимального правдоподобия и максимума апостериорной вероятности
- •1.8. Метод инструментальных переменных
- •1.9. Реализация метода наименьших квадратов в пакете matlab
- •1.10. Метод стохастической аппроксимации
- •Контрольные задания
- •Глава 2 Непараметрические регрессионные модели
- •2.1. Непараметрическая оценка плотности распределения вероятностей Розенблатта–Парзена
- •2.2. Непараметрическая оценка регрессии Надарая–Ватсона
- •Контрольные задания
- •Глава 3 модели линейных динамических систем
- •3.1. Способы описания линейных динамических систем
- •3.2. Модель динамической системы в виде представления Фурье (модель сигнала)
- •3.3. Частотный метод описания линейных динамических систем
- •3.4. Определение передаточной функции линейных динамических систем на основе спектральных плотностей
- •Контрольные задания
- •Глава 4 непараметрические модели линейных динамических систем
- •4.1. Постановка задачи идентификации линейных динамических систем
- •4.2. Математическое описание и построение непараметрической модели линейных динамических систем
- •4.3. Оптимизация непараметрических моделей линейных динамических систем
- •4.4. Непараметрические модели линейных динамических систем на основе уравнения Винера–Хопфа
- •Контрольные задания
- •Заключение
- •Библиографический список
- •Англо-русский словарь терминов
- •Сходимость статистических оценок
- •660041, Г. Красноярск, пр. Свободный, 79.
- •660041, Г. Красноярск, пр. Свободный, 82а.
Контрольные задания
Дайте определения понятий «регрессия» и «регрессионный анализ».
Покажите связь между понятием среднего и наилучшим приближением в среднеквадратическом смысле.
Запишите уравнение МНК для линейного случая в матричной форме.
Найдите коэффициенты уравнения регрессии y = ax + b методом МНК по следующей выборке измерений входной и выходной величин: (0, 0), (1, 1), (2, 1).
Используя первые три ортогональных полинома Лежандра, определите коэффициенты уравнения регрессии методом МНК по следующей выборке измерений входной и выходной величин: (–1; 0), (–0,5; 3), (0; 4,5), (0,5; 5,5), (1; 6).
Докажите лемму об обращении матриц.
Проделайте три итерации рекуррентным алгоритмом МНК, используя исходные данные из задания 4 и начальные значения параметров: a0 = 0, b0 = 1.
Примените линейную аппроксимацию МНК для определения коэффициента нелинейного уравнения модели y = ax по следующей выборке: (0, 1), (1, 2), (2, 4). Начальное значение x0 = 1.
В открытых источниках найдите информацию о динамике численности населения в России за последние 20 лет. Постройте полиномиальную модель четвертого порядка методом МНК, используя пакет MATLAB. На основании построенной модели предскажите численность населения через 10 лет.

Глава 2 Непараметрические регрессионные модели
В данной главе предлагаются сведения о непараметрических моделях статических объектов. Вводятся понятия ядерной функции и параметра размытости. На основании непараметрической оценки плотности вероятности строится оценка парной и множественной регрессии для статического случая. Дается представление о свойствах и особенностях реализации непараметрических моделей регрессионного типа, предлагается способ оптимизации моделей по параметрам размытости.
2.1. Непараметрическая оценка плотности распределения вероятностей Розенблатта–Парзена
Функцией распределения вещественной случайной величины T называется вероятность того, что эта величина принимает меньшее значение, чем аргумент функции:
|
(2.1) |
Функция распределения возрастает на всей области определения и принимает значения от 0 до 1 (рис. 2.1).
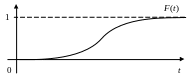
Рис. 2.1. Функция распределения вероятности
Плотностью распределения случайной величины называется первая производная от функции распределения (рис. 2.2):
|
(2.2) |
Плотность распределения удовлетворяет следующему свойству:
|
(2.3) |
Пусть задана
выборка случайной величины T:
![]() .
Если использовать эту выборку, то можно
получить следующий вариант оценки
функции распределения:
.
Если использовать эту выборку, то можно
получить следующий вариант оценки
функции распределения:
|
(2.4) |
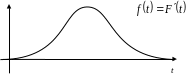
Рис. 2.2. Плотность распределения вероятности
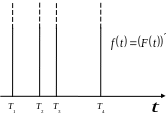
Предположим, что выборочные данные будут равновероятными. Тогда оценка функции распределения может быть представлена как оценка функции распределения дискретной случайной величины (рис. 2.3):
. . . . . . . . |
(2.5) |
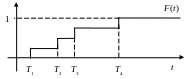
Рис. 2.3. Оценка функции распределения
дискретной случайной величины (S = 4)
Единичной
ступенчатой функцией Хевисайда
![]() (рис. 2.4) назовем функцию
(рис. 2.4) назовем функцию
|
(2.6) |
Дельта-функцией
Дирака
![]() (см. рис. 2.4) называется первая производная
от функции Хевисайда:
(см. рис. 2.4) называется первая производная
от функции Хевисайда:
|
(2.7) |
Дельта-функция удовлетворяет следующим свойствам:
|
где
![]() ;
;
![]() – произвольная функция, принимающая
конечные значения.
– произвольная функция, принимающая
конечные значения.
Применяя операцию дифференцирования к дискретной функции распределения, получим следующую оценку плотности распределения (рис. 2.5):
|
(2.8) |
|
|
Рис. 2.4. Функции Дирака и Хевисайда
|
Рис. 2.5. Несостоятельная оценка плотности распределения |
Приведенная выше
оценка плотности распределения является
несмещенной,
но в то же время несостоятельной
(см. приложение).
Для того чтобы сгенерировать состоятельную
оценку и обеспечить ее практическую
применимость, необходима ее модификация.
Модификация заключается в размытии
входящих в оценку дельта-функций (рис.
2.6). В результате модификации получаем
ядерную,
или
колоколообразную функцию
![]() :
:
|
(2.9) |
где
![]() – параметр, определяющий степень
размытости ядерной функции, т. е. гладкость
оценки. Параметр
удовлетворяет следующим условиям:
– параметр, определяющий степень
размытости ядерной функции, т. е. гладкость
оценки. Параметр
удовлетворяет следующим условиям:
|
|
О
Рис. 2.6. Трансформация ядерной функ-
ции
в зависимости от параметра
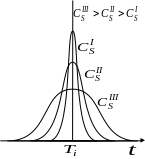 т
ядерной функции потребуем выполнения
тех же самых соотношений, что и для
дельта-функции:
т
ядерной функции потребуем выполнения
тех же самых соотношений, что и для
дельта-функции:
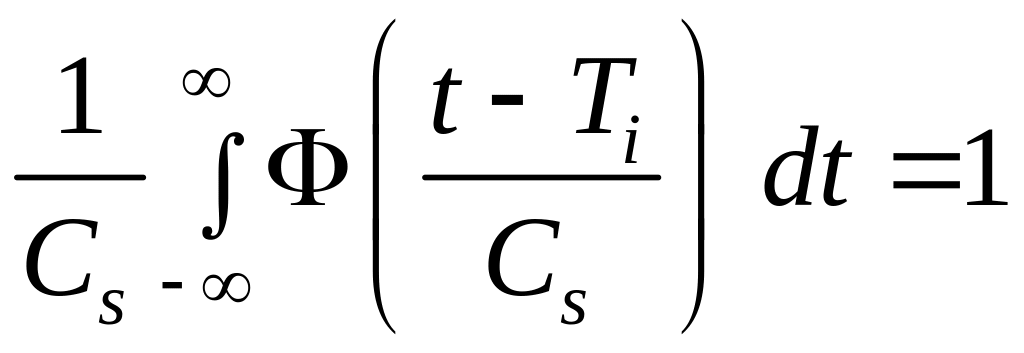 ,
,
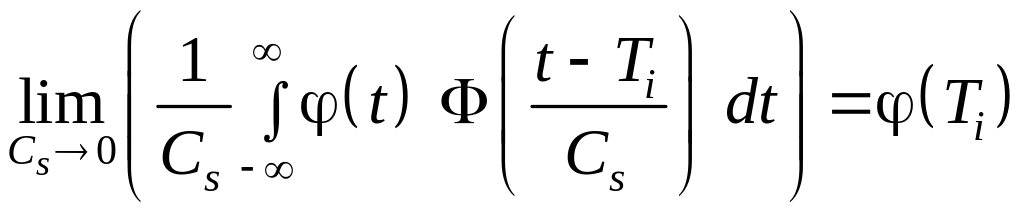 .
.
В качестве ядерных могут быть использованы следующие функции:
– экспоненциальная функция (функция Гаусса):
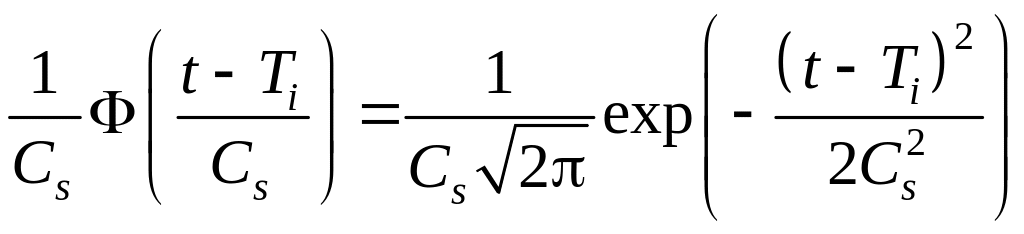 ;
;
– параболическая функция:
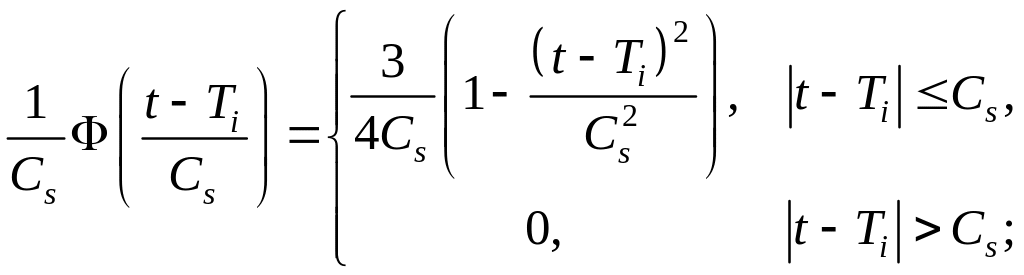
– прямоугольная функция:
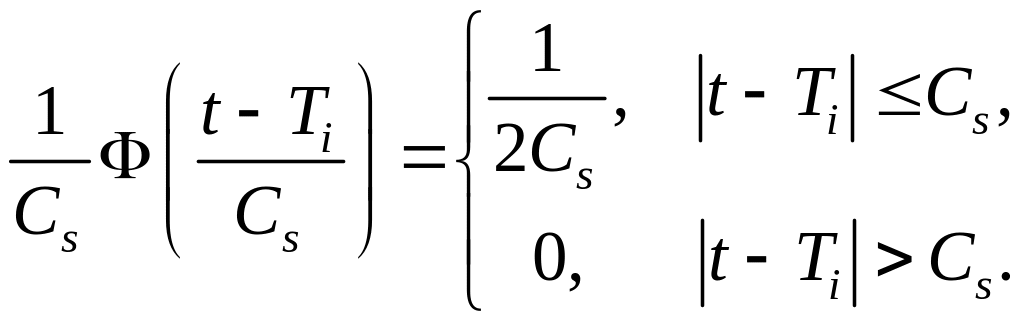
Окончательно получим непараметрическую оценку плотности распределения:
|
(2.10) |
Первым подобную оценку ввел М. Розенблатт в 1957 г., а Е. Парзен в 1962 г. ее уточнил. Эта оценка положила начало непараметрической теории, которая применяется для решения задач, связанных с обработкой статистических данных, идентификации, управления и распознавания образов. Оценка плотности – асимптотически несмещенная и сходится в среднеквадратическом (см. приложение).
Пусть
дана многомерная случайная величина
T,
т. е. задан вектор размерности k:
![]() ,
тогда оценкой плотности будет следующая
статистика:
,
тогда оценкой плотности будет следующая
статистика:
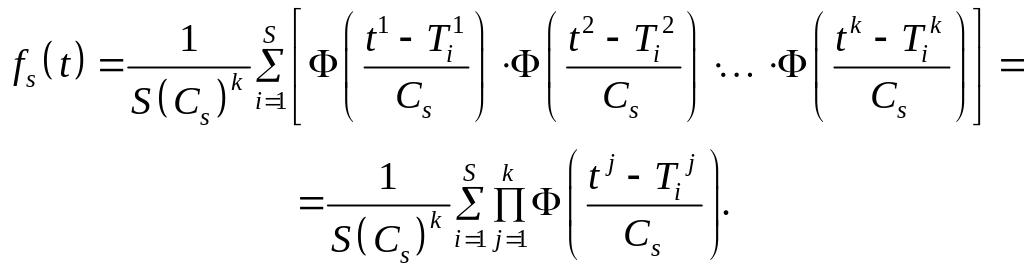
Параметры могут быть различными для разных компонентов многомерной случайной величины. Пусть – вектор размерности k:
![]() .
.
Тогда оценка плотности примет вид
|
(2.11) |
Оценка плотности вероятности входит в выражения для вычисления всевозможных характеристик случайных величин. Рассмотрим ее применение в задачах регрессионного анализа.


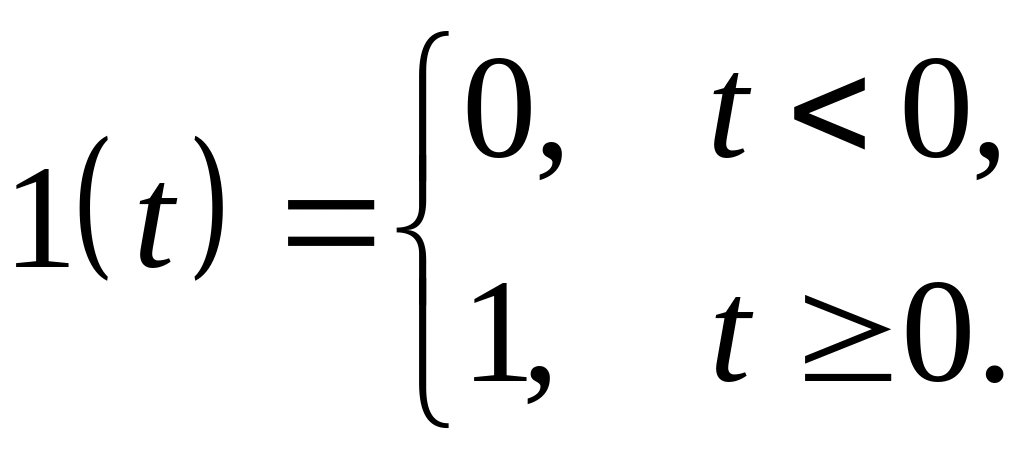
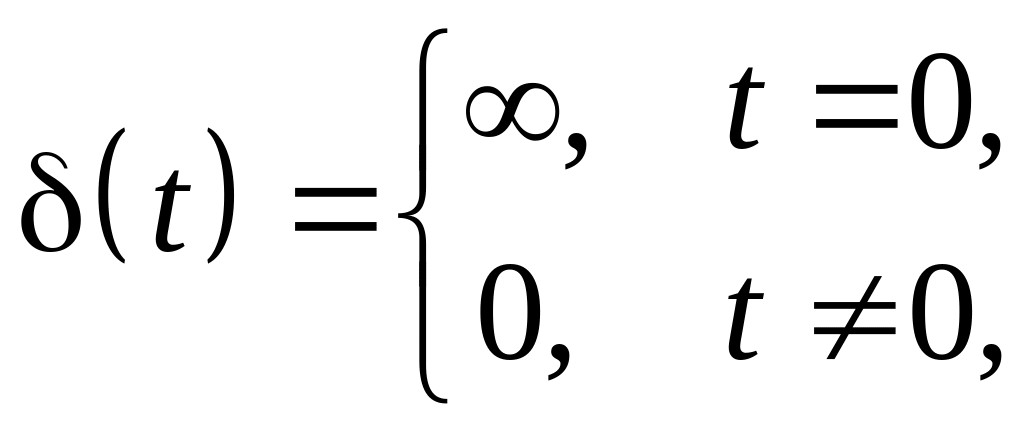
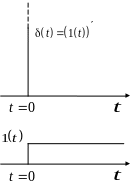
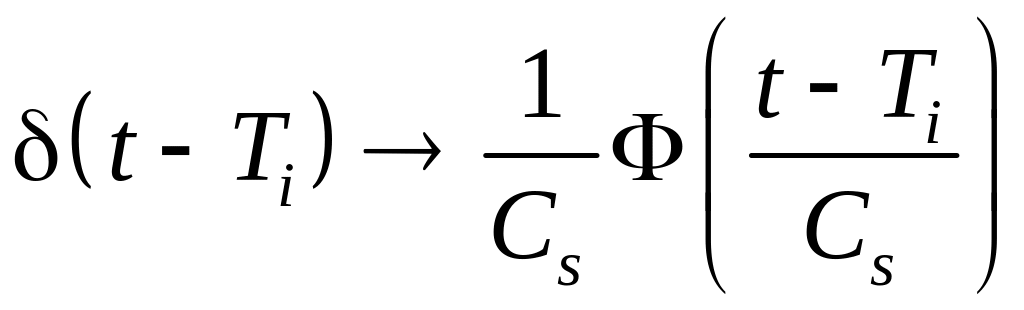 ,
,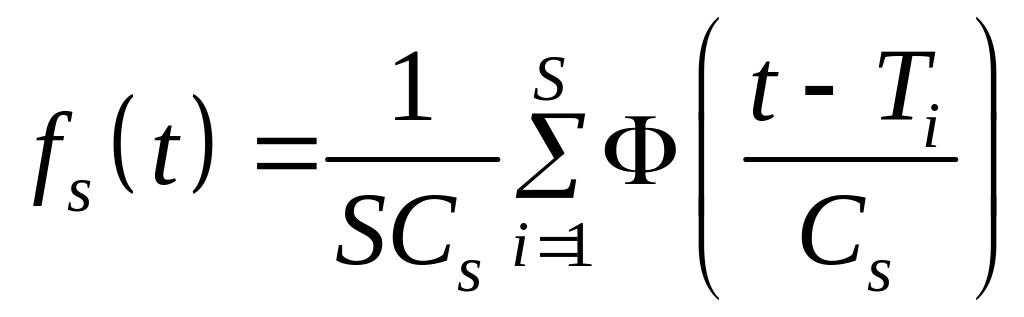 .
.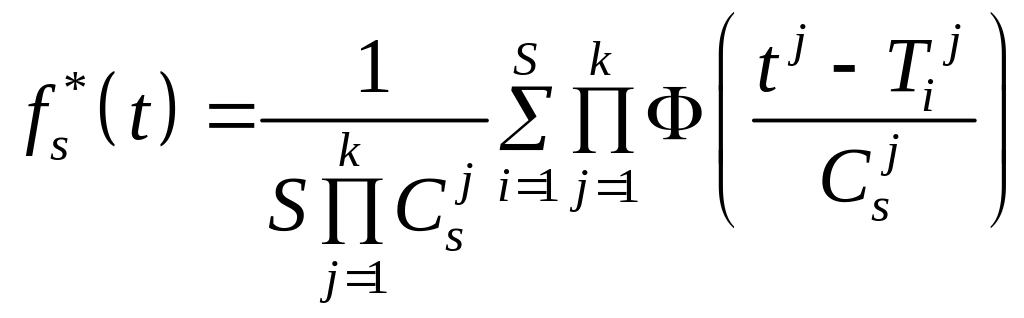 .
.