
- •Е. Д. Агафонов, о. В. Шестернёва Математическое моделирование линейных динамических систем
- •© Сибирский федеральный университет, 2011
- •Оглавление
- •Предисловие
- •Глава 1 Параметрические регрессионные модели
- •1.1. Линейная регрессия
- •1.2. Метод наименьших квадратов. Критерий метода наименьших квадратов
- •1.3. Идентификация линейных по параметрам моделей с использованием метода наименьших квадратов
- •1.4. Линейный метод наименьших квадратов с использованием ортогональных полиномов
- •1.5. Рекуррентный метод наименьших квадратов
- •1.6. Линейная аппроксимация метода наименьших квадратов
- •1.7. Методы максимального правдоподобия и максимума апостериорной вероятности
- •1.8. Метод инструментальных переменных
- •1.9. Реализация метода наименьших квадратов в пакете matlab
- •1.10. Метод стохастической аппроксимации
- •Контрольные задания
- •Глава 2 Непараметрические регрессионные модели
- •2.1. Непараметрическая оценка плотности распределения вероятностей Розенблатта–Парзена
- •2.2. Непараметрическая оценка регрессии Надарая–Ватсона
- •Контрольные задания
- •Глава 3 модели линейных динамических систем
- •3.1. Способы описания линейных динамических систем
- •3.2. Модель динамической системы в виде представления Фурье (модель сигнала)
- •3.3. Частотный метод описания линейных динамических систем
- •3.4. Определение передаточной функции линейных динамических систем на основе спектральных плотностей
- •Контрольные задания
- •Глава 4 непараметрические модели линейных динамических систем
- •4.1. Постановка задачи идентификации линейных динамических систем
- •4.2. Математическое описание и построение непараметрической модели линейных динамических систем
- •4.3. Оптимизация непараметрических моделей линейных динамических систем
- •4.4. Непараметрические модели линейных динамических систем на основе уравнения Винера–Хопфа
- •Контрольные задания
- •Заключение
- •Библиографический список
- •Англо-русский словарь терминов
- •Сходимость статистических оценок
- •660041, Г. Красноярск, пр. Свободный, 79.
- •660041, Г. Красноярск, пр. Свободный, 82а.
4.2. Математическое описание и построение непараметрической модели линейных динамических систем
Известные методы идентификации линейных динамических систем имеют один существенный недостаток: эти методы могут быть применимы на практике только в том случае, когда объект идентификации очень хорошо изучен, т. е. известны тип и порядок уравнения или системы дифференциальных уравнений, описывающие данный объект. Однако во многих практических задачах нередко встречаются такие системы, точного описания которых по каким-либо причинам не существует. В таких случаях необходимо использовать методы идентификации в условиях неполной информации, например из класса непараметрических моделей.
Суть метода
построения непараметрической модели
ЛДС заключается в следующем: известно,
что реакция ЛДС
на входное
воздействие
![]() описывается интегралом Дюамеля
описывается интегралом Дюамеля
![]() .
(4.1)
.
(4.1)
Вычисление значения
выхода объекта
![]() при этом возможно, если известна его
весовая функция
h(t).
Но для
реального объекта невозможно или очень
сложно получить такую функцию. Поэтому
основная идея идентификации ЛДС в
условиях непараметрической неопределенности
состоит в непараметрическом оценивании
весовой функции.
при этом возможно, если известна его
весовая функция
h(t).
Но для
реального объекта невозможно или очень
сложно получить такую функцию. Поэтому
основная идея идентификации ЛДС в
условиях непараметрической неопределенности
состоит в непараметрическом оценивании
весовой функции.
Пусть
на вход ЛДС подано единичное ступенчатое
воздействие 1(t),
![]() ,
где
,
где
![]() – время окончания переходного процесса;
1(t)
– функция Хевисайда. Обозначим через
– время окончания переходного процесса;
1(t)
– функция Хевисайда. Обозначим через
![]() реализацию наблюдений входа-выхода
объекта, причем наблюдения выходной
переменной
осуществляются
в дискретные моменты времени через
интервал
реализацию наблюдений входа-выхода
объекта, причем наблюдения выходной
переменной
осуществляются
в дискретные моменты времени через
интервал
![]() со случайной статистически независимой
помехой. Непараметрическая оценка
интеграла Дюамеля при ненулевых начальных
условиях в общем виде будет выглядеть
следующим образом:
со случайной статистически независимой
помехой. Непараметрическая оценка
интеграла Дюамеля при ненулевых начальных
условиях в общем виде будет выглядеть
следующим образом:
 ,
(4.2)
,
(4.2)
где
![]() ,
,
![]() – соответственно оценки переходной и
весовой функции системы.
– соответственно оценки переходной и
весовой функции системы.
Значения переходной k(t) есть не что иное, как кривая регрессии. Существует непараметрический метод оценки кривой регрессии, общий вид которого для скалярной величины выглядит следующим образом:
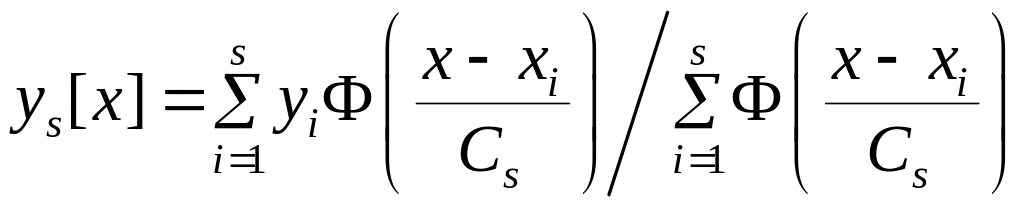 ,
(4.3)
,
(4.3)
где
![]() –
непараметрическая оценка регрессии
–
непараметрическая оценка регрессии
![]() ;
Ф( )
– колоколообразная,
или ядерная функция. Функция Ф( )
должна
удовлетворять условиям
;
Ф( )
– колоколообразная,
или ядерная функция. Функция Ф( )
должна
удовлетворять условиям
![]()
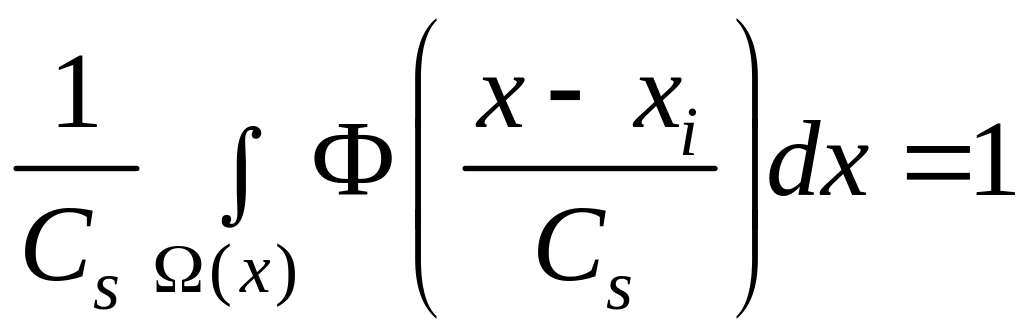 ,
,
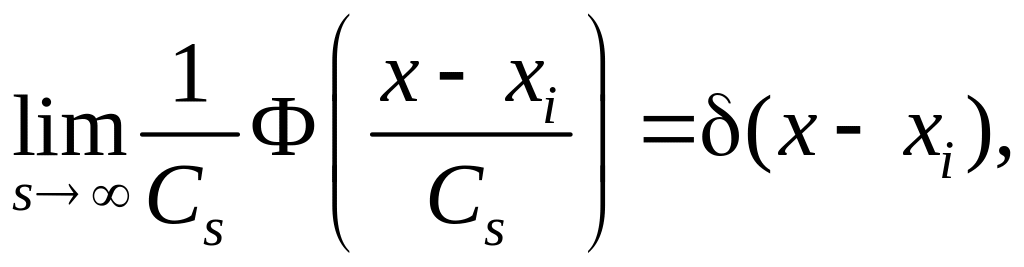 (4.4)
(4.4)
а параметр размытости Сs – условиям
![]() (4.5)
(4.5)
В качестве примера приведем возможные виды функций Ф(u):

(4.6)
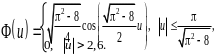
(4.7)
В
оценке (4.3) точки xi
располагаются
на различном расстоянии, т. е. шаг
![]() не является константой. Произведем
генерацию новой выборки
не является константой. Произведем
генерацию новой выборки
![]() с
постоянным шагом
,
состоящей из s
элементов
с
постоянным шагом
,
состоящей из s
элементов
![]() .
Тогда оценка регрессии примет вид
.
Тогда оценка регрессии примет вид
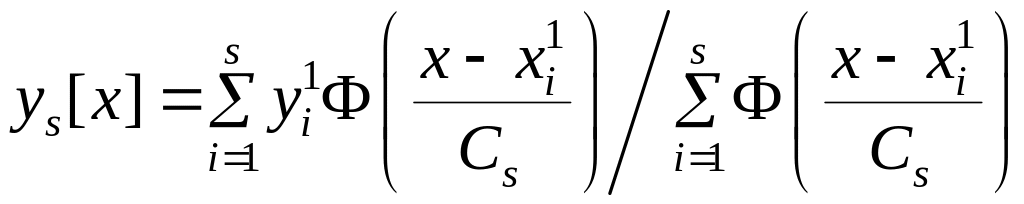 .
(4.8)
.
(4.8)
Домножим
числитель и знаменатель на
![]()
 .
(4.9)
.
(4.9)
Отметим,
что знаменатель в формуле (4.9) – это
оценка плотности вероятности
![]() ,
а так как шаг
,
а так как шаг
![]() постоянный, то и оценка
тоже будет постоянной:
постоянный, то и оценка
тоже будет постоянной:
![]() .
Внесем эту константу в функцию Ф( )
и
получим новую колоколообразную функцию
Н(
):
.
Внесем эту константу в функцию Ф( )
и
получим новую колоколообразную функцию
Н(
):
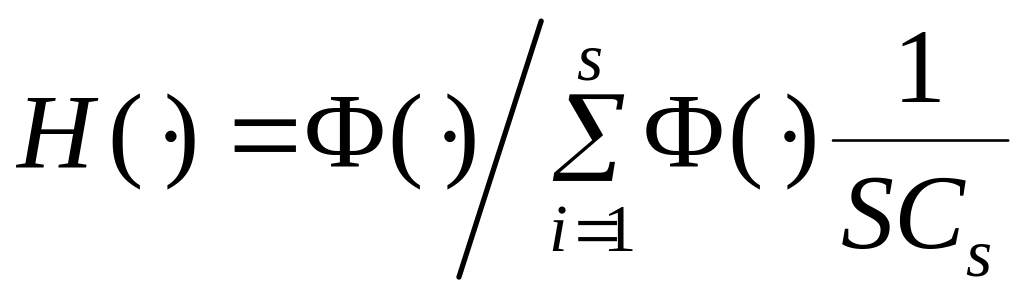 .
(4.10)
.
(4.10)
С учетом (4.10) оценка кривой регрессии приобретет вид
 .
(4.11)
.
(4.11)
Будем
считать, что значения переходной функции
![]() представляют собой регрессию, а шаг
дискретизации
постоянен. Тогда оценка переходной
функции будет следующей:
представляют собой регрессию, а шаг
дискретизации
постоянен. Тогда оценка переходной
функции будет следующей:
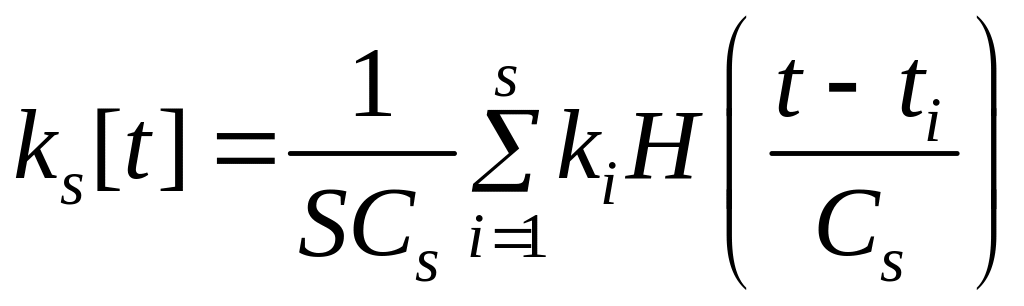 ,
(4.12)
,
(4.12)
где
–
дискретные измерения значений переходной
характеристики ЛДС;
![]() –
колоколообразная функция;
– параметр размытости.
–
колоколообразная функция;
– параметр размытости.
Переходная функция k(t) связана с весовой функцией, производной по времени:
![]() .
.
Тогда непараметрическая оценка весовой функции примет следующий вид:
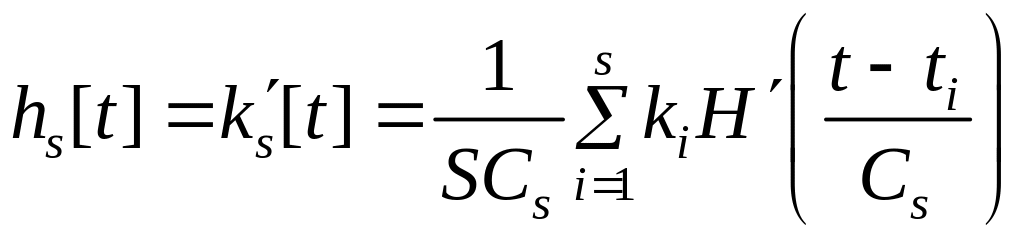 .
(4.13)
.
(4.13)
Подставив эту оценку в интеграл Дюамеля, получим непараметрическую модель ЛДС:
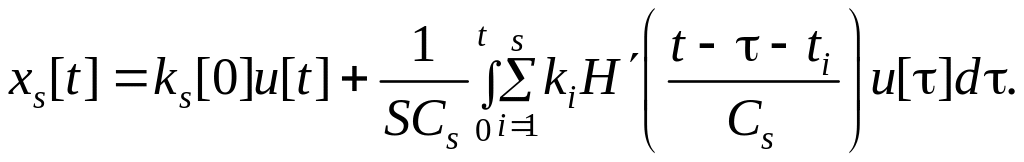 (4.14)
(4.14)
При программной реализации этой модели воспользуемся численным методом прямоугольников:
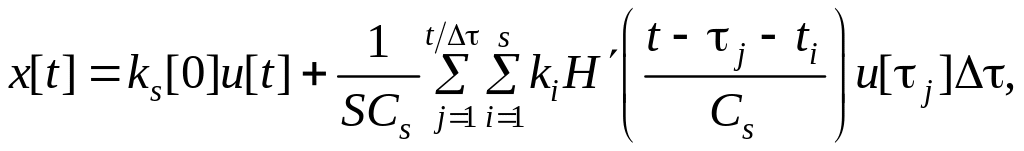 (4.15)
(4.15)
где
τ – переменная интегрирования, которая
изменяется с дискретностью
![]() (
(![]() ).
).
В
непараметрической модели колоколообразные
функции
![]() и параметр размытости Cs
должны
удовлетворять следующим условиям
сходимости:
и параметр размытости Cs
должны
удовлетворять следующим условиям
сходимости:
а)
![]() ;
;
б)
![]() ;
;
в)
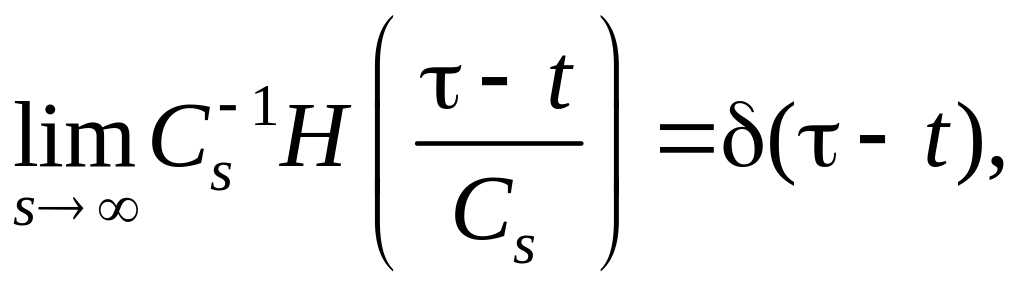
 ,
,
![]()
![]()
![]() .
.
Существует ряд функций , удовлетворяющих данным условиям, которые можно использовать при расчетах:
– функция косинуса:
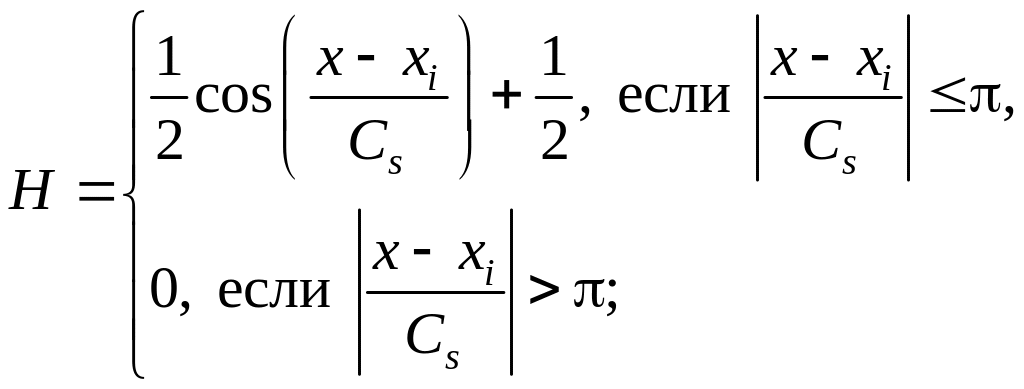 (4.16)
(4.16)
– функция Соболева:
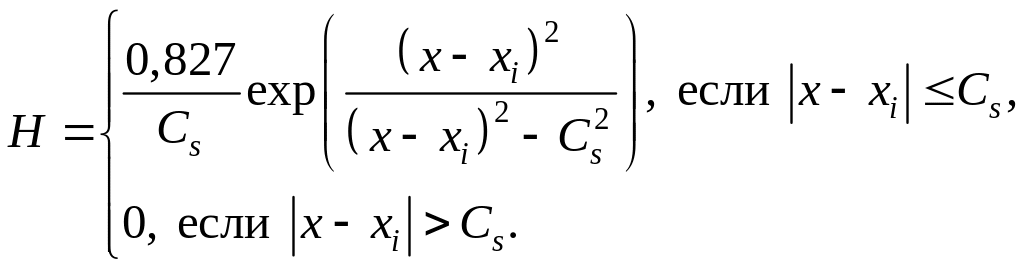 (4.17)
(4.17)
Эти функции могут использоваться при оценке производных, так как они многократно дифференцируемы (рис. 4.2).
Исследование влияния вида колоколообразных функций на точность оценивания привело к выводу, что вид этих функций незначительно влияет на точность аппроксимаций. Поэтому для облегчения расчетов можно брать любые виды колоколообразных функций, широко применяемые в непараметрическом оценивании, в том числе треугольные, параболические и др., если они удовлетворяют приведенным выше условиям сходимости. В качестве производных функции могут быть использованы не аналитические выражения, а их кусочно-постоянные аналоги, определяемые при помощи метода графического дифференцирования. В этом методе величина ступеньки в кусочно-постоянном аналоге определяется исходя из выполнения условий сходимости (рис. 4.3).
Оценка
весовой функции, где в качестве производной
колоколообразной функции
![]() используется ее кусочно-постоянный
аналог, имеет следующий вид:
используется ее кусочно-постоянный
аналог, имеет следующий вид:
![]() ,
(4.18)
,
(4.18)
где
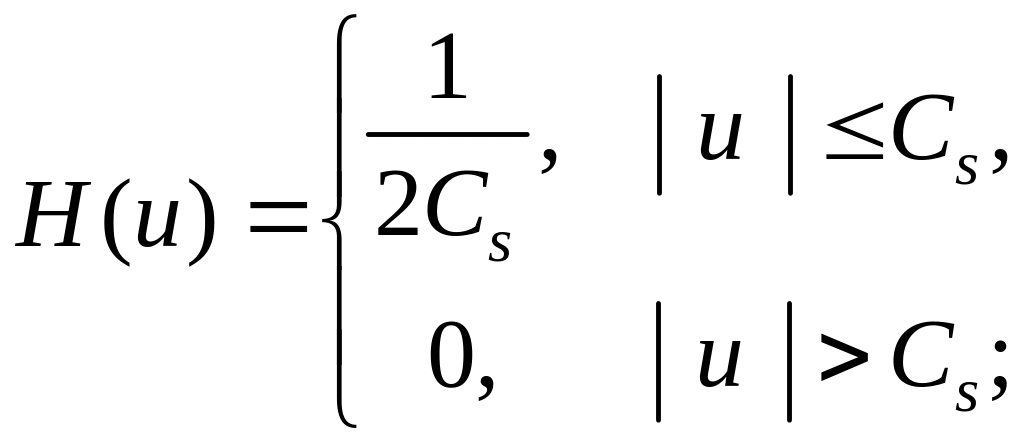 (4.19)
(4.19)
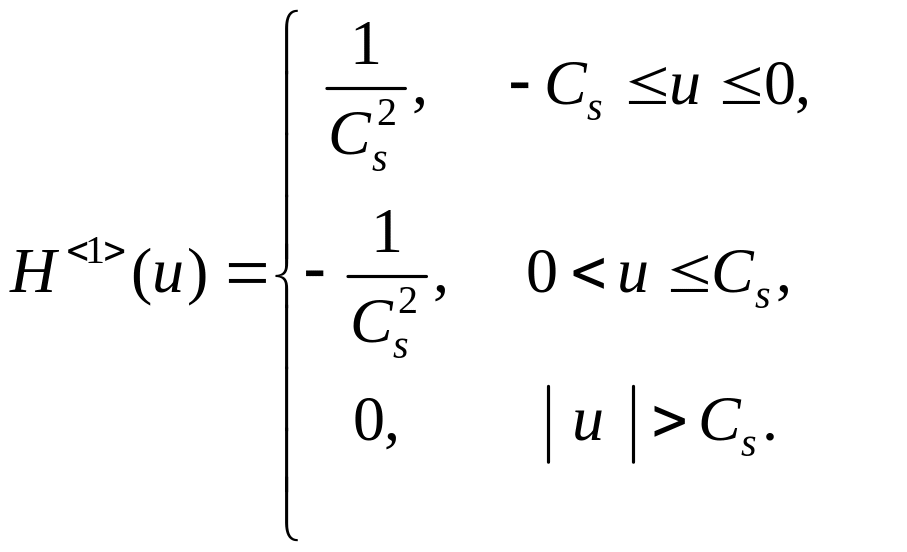 (4.20)
(4.20)

Рис. 4.2. График колоколообразной функции
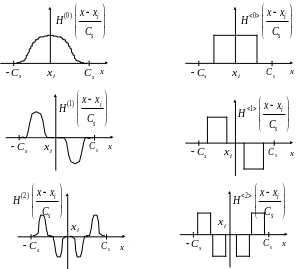
Рис. 4.3. Функция Соболева, ее производные и кусочно-постоянные
аналоги производных (обозначены
![]() )
)
Таким образом, использование кусочно-постоянных аналогов позволяет расширить класс колоколообразных функций при построении непараметрических моделей ЛДС.
