
- •Е. Д. Агафонов, о. В. Шестернёва Математическое моделирование линейных динамических систем
- •© Сибирский федеральный университет, 2011
- •Оглавление
- •Предисловие
- •Глава 1 Параметрические регрессионные модели
- •1.1. Линейная регрессия
- •1.2. Метод наименьших квадратов. Критерий метода наименьших квадратов
- •1.3. Идентификация линейных по параметрам моделей с использованием метода наименьших квадратов
- •1.4. Линейный метод наименьших квадратов с использованием ортогональных полиномов
- •1.5. Рекуррентный метод наименьших квадратов
- •1.6. Линейная аппроксимация метода наименьших квадратов
- •1.7. Методы максимального правдоподобия и максимума апостериорной вероятности
- •1.8. Метод инструментальных переменных
- •1.9. Реализация метода наименьших квадратов в пакете matlab
- •1.10. Метод стохастической аппроксимации
- •Контрольные задания
- •Глава 2 Непараметрические регрессионные модели
- •2.1. Непараметрическая оценка плотности распределения вероятностей Розенблатта–Парзена
- •2.2. Непараметрическая оценка регрессии Надарая–Ватсона
- •Контрольные задания
- •Глава 3 модели линейных динамических систем
- •3.1. Способы описания линейных динамических систем
- •3.2. Модель динамической системы в виде представления Фурье (модель сигнала)
- •3.3. Частотный метод описания линейных динамических систем
- •3.4. Определение передаточной функции линейных динамических систем на основе спектральных плотностей
- •Контрольные задания
- •Глава 4 непараметрические модели линейных динамических систем
- •4.1. Постановка задачи идентификации линейных динамических систем
- •4.2. Математическое описание и построение непараметрической модели линейных динамических систем
- •4.3. Оптимизация непараметрических моделей линейных динамических систем
- •4.4. Непараметрические модели линейных динамических систем на основе уравнения Винера–Хопфа
- •Контрольные задания
- •Заключение
- •Библиографический список
- •Англо-русский словарь терминов
- •Сходимость статистических оценок
- •660041, Г. Красноярск, пр. Свободный, 79.
- •660041, Г. Красноярск, пр. Свободный, 82а.
4.4. Непараметрические модели линейных динамических систем на основе уравнения Винера–Хопфа
Рассмотрим постановку задачи идентификации ЛДС (см. п. 4.1) в условиях нормального функционирования объекта. В этом случае имеется возможность лишь наблюдать за объектом, а постановка эксперимента не возможна (пассивный эксперимент). Данные о структуре объекта отсутствуют. Необходимо построить математическую модель стохастического объекта, адекватно описывающую его поведение при произвольном входном воздействии с использованием уравнения Винера–Хопфа.
Идентификация при пассивном эксперименте имеет большое значение с практической точки зрения, поскольку вмешательство в ход нормального функционирования объекта не всегда желательно. В этом случае следует применять метод определения импульсной переходной характеристики с использованием уравнения Винера–Хопфа
![]() , (4.27)
, (4.27)
где
![]() и
и
![]() –
соответственно автокорреляционная
и взаимная
корреляционная функции.
–
соответственно автокорреляционная
и взаимная
корреляционная функции.
Идентификация в условиях нормального функционирования сводится к нахождению весовой функции из уравнения Винера–Хопфа на основе наблюдений входа-выхода объекта, где в качестве взаимной и автокорреляционной функции используются их оценки.
Функцию, значение которой при каждом значении независимой переменной является случайной величиной, называют случайной функцией. Случайные функции, для которых независимой переменной является время t, называют случайными, или стохастическими процессами.
Случайный процесс
![]() является множеством определенных кривых
является множеством определенных кривых
![]() ,
где
,
получаемых в результате отдельных
опытов. Каждую кривую этого множества
называют реализацией
случайного процесса.
,
где
,
получаемых в результате отдельных
опытов. Каждую кривую этого множества
называют реализацией
случайного процесса.
Приведем основные характеристики случайного процесса.
Математическое
ожидание
(среднее значение) случайного процесса
есть функция
![]() :
:
![]() ,
(4.28)
,
(4.28)
где
![]() – одномерная плотность вероятности
случайного процесса
.
– одномерная плотность вероятности
случайного процесса
.
Математическое ожидание случайного процесса представляет собой некоторую неслучайную (регулярную) функцию времени , около которой группируются и относительно которой колеблются все реализации данного случайного процесса.
Для того чтобы каким-то образом учесть степень разброса реализаций случайного процесса относительно его среднего значения, вводят понятие «дисперсия случайного процесса», которая равна математическому ожиданию квадрата центрированного случайного процесса:
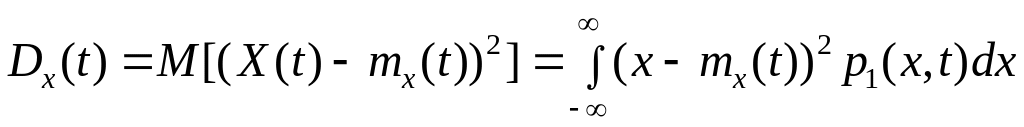 .
(4.29)
.
(4.29)
Дисперсия случайного процесса есть такая функция, значение которой при каждом данном значении аргумента равно дисперсии значения случайной функции при этом значении аргумента.
Математическое ожидание и дисперсия являются важными характеристиками случайного процесса, но они не дают достаточного представления о том, какой характер будут иметь отдельные реализации случайного процесса.
Чтобы охарактеризовать внутреннюю структуру случайного процесса, т. е. учесть связь между значениями случайного процесса в различные моменты времени, или степень изменчивости случайного процесса, необходимо ввести понятие «корреляционная (автокорреляционная) функция случайного процесса».
Корреляционной
функцией случайного процесса
называют неслучайную функцию двух
аргументов
![]() ,
которая для каждой пары произвольно
выбранных значений аргументов (моментов
времени)
,
которая для каждой пары произвольно
выбранных значений аргументов (моментов
времени)
![]() и
и
![]() равна математическому ожиданию
произведения двух случайных величин
равна математическому ожиданию
произведения двух случайных величин
![]() и
и
![]() соответствующих
сечений случайного процесса:
соответствующих
сечений случайного процесса:
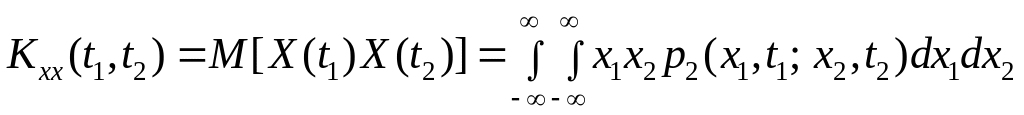 .
(4.30)
.
(4.30)
Здесь под знаком
интеграла стоит плотность
![]() совместного распределения случайных
величин.
совместного распределения случайных
величин.
Различные случайные процессы в зависимости от того, как изменяются их статистические характеристики с течением времени, делят на стационарные и нестационарные.
Случайный процесс X(t) называется стационарным в узком смысле, если закон распределения не зависит от времени.
Стационарным в широком смысле называют случайный процесс , математическое ожидание которого постоянно:
![]()
![]() ,
(4.31)
,
(4.31)
а корреляционная
функция зависит от единственной
переменной – разности аргументов
![]() :
:
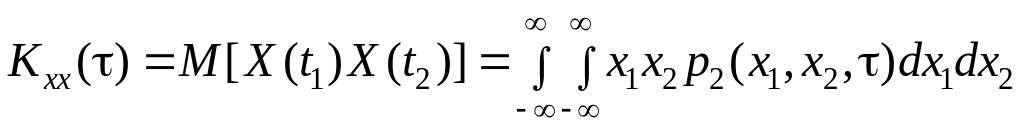 .
(4.32)
.
(4.32)
Следует различать два типа средних значений: среднее по множеству и среднее по времени. Первый из этих типов описан выше. Второй тип может быть получен путем обработки одной реализации случайного процесса. Понятие среднего по времени является обобщением понятия среднего арифметического значений xi процесса в различные моменты времени:
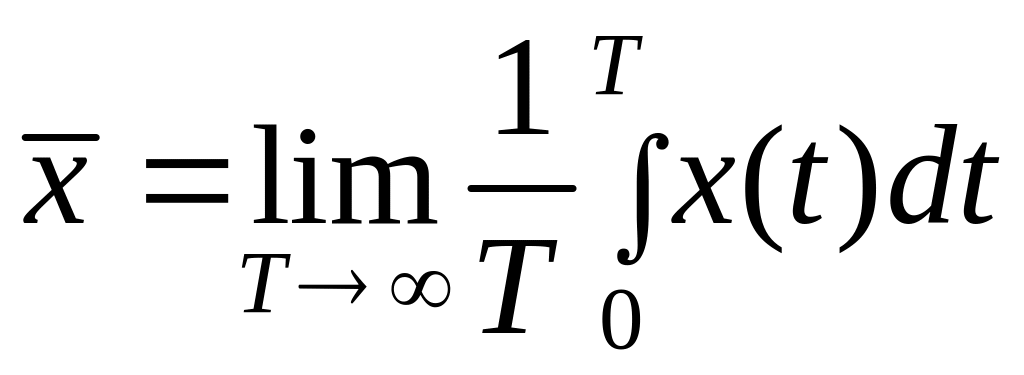 .
(4.33)
.
(4.33)
Существует класс случайных процессов, называемых эргодическими, которые обладают весьма важным свойством.
Случайный процесс называется эргодическим, если с вероятностью, равной единице, среднее по множеству от величины, характеризующей процесс, равно среднему по времени.
Напомним, что среднее по множеству получается для ансамбля экземпляров случайного процесса и для стационарного процесса оно не зависит от времени. Между тем среднее по времени определяется для одного экземпляра случайного процесса и поэтому, вообще говоря, является случайной величиной в зависимости от того, какой экземпляр появился в том или другом испытании. Тот факт, что эти две столь различные величины совпадают с вероятностью 1, справедлив лишь для эргодических процессов.
На практике часто весьма затруднительно установить эргодичность экспериментально исследуемого случайного процесса. Однако для ряда процессов физические соображения позволяют высказать гипотезу об их эргодичности. Любую бесконечную кривую экземпляра случайного процесса можно разрезать на сколь угодно большое количество достаточно длинных кусков. А поскольку процесс стационарный, то вероятностные свойства этих кусков одинаковы. Допустим, что их можно рассматривать как экземпляры случайного процесса, принадлежащие одному ансамблю. Это равносильно утверждению о том, что с течением времени одна и та же кривая будет копировать любой кусок какого-либо другого экземпляра случайного процесса. В этом смысле один бесконечно длинный экземпляр эквивалентен бесконечному множеству различных достаточно длинных экземпляров процесса. Разница между различными экземплярами состоит лишь в том, что различные куски в них расположены в различном порядке. Поэтому безразлично, проводить ли усреднение по времени или в некоторый момент времени по множеству различных экземпляров, так как при любом способе усреднения одни и те же значения будут встречаться с одинаковыми частотами.
При вычислении характеристик эргодического процесса (например, корреляционной функции) неважно, будет ли производиться усреднение по времени или в некоторый момент времени по множеству различных реализаций. Корреляционные функции эргодического процесса имеют следующий вид:
![]() ,
(4.34)
,
(4.34)
![]() .
(4.35)
.
(4.35)
Построение
непараметрической модели ЛДС в условиях
нормального функционирования объекта
основывается на оценках корреляционных
функций. Пусть
на вход ЛДС поступает сигнал
![]() ,
где
,
где
![]() – регулярный вход;
– регулярный вход;
![]() – случайная величина, распределенная
равномерно на интервале
– случайная величина, распределенная
равномерно на интервале
![]() ;
;
![]() – аддитивная помеха, статистически
независимая, с нулевым средним и
ограниченной дисперсией. Тогда выходом
системы будет функция
– аддитивная помеха, статистически
независимая, с нулевым средним и
ограниченной дисперсией. Тогда выходом
системы будет функция
![]() ,
где
,
где
![]() – реакция
объекта на сиг-
нал
;
– реакция
объекта на сиг-
нал
;
![]() – реакция объекта на сигнал
;
– реакция объекта на сигнал
;
![]() – аддитивная помеха, статистически
независимая, с нулевым средним и
ограниченной дисперсией. Очевидно, что
– аддитивная помеха, статистически
независимая, с нулевым средним и
ограниченной дисперсией. Очевидно, что
![]() ,
,
следовательно,
![]() .
.
Поэтому, имея
![]() реализаций
,
оценим
реализаций
,
оценим
![]() и получим
реализации
со случайной
помехой
:
и получим
реализации
со случайной
помехой
:
![]() .
(4.36)
.
(4.36)
Пусть случайные
процессы
![]() и
эргодические и имеется
реализаций процессов
и
на интервале
и
эргодические и имеется
реализаций процессов
и
на интервале
![]() с шагом
с шагом
![]() :
:
![]() .
.
Тогда оценки
корреляционных функций на интервале
![]() будут иметь вид
будут иметь вид
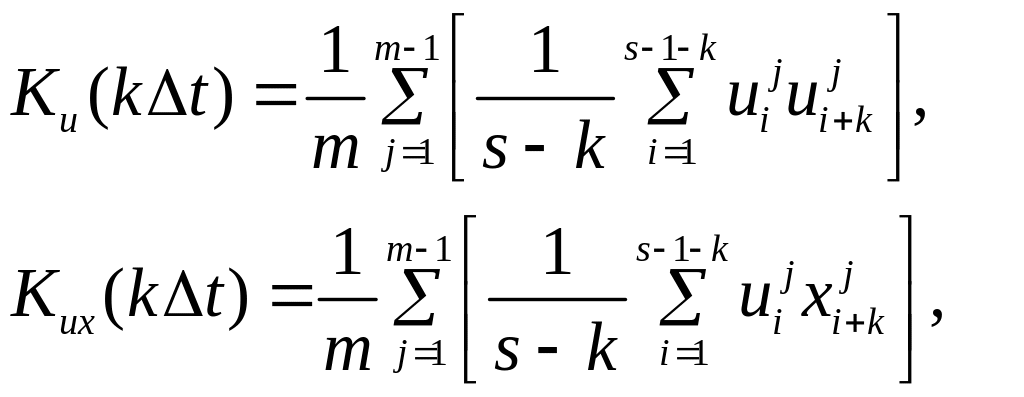 (4.37)
(4.37)
где
![]() .
.
Для построения модели ЛДС воспользуемся уравнением Винера–Хопфа
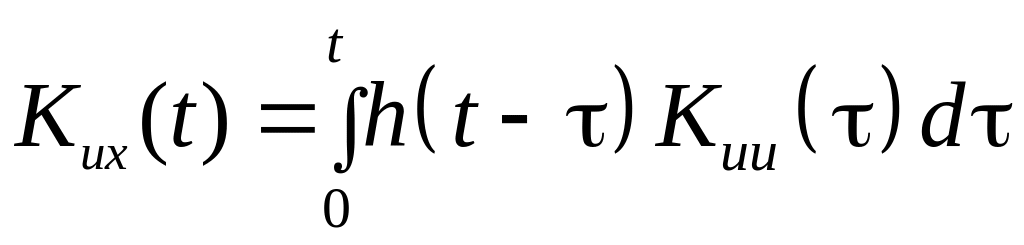 . (4.38)
. (4.38)
Определение импульсной характеристики заключается в численном решении уравнения Винера–Хопфа:
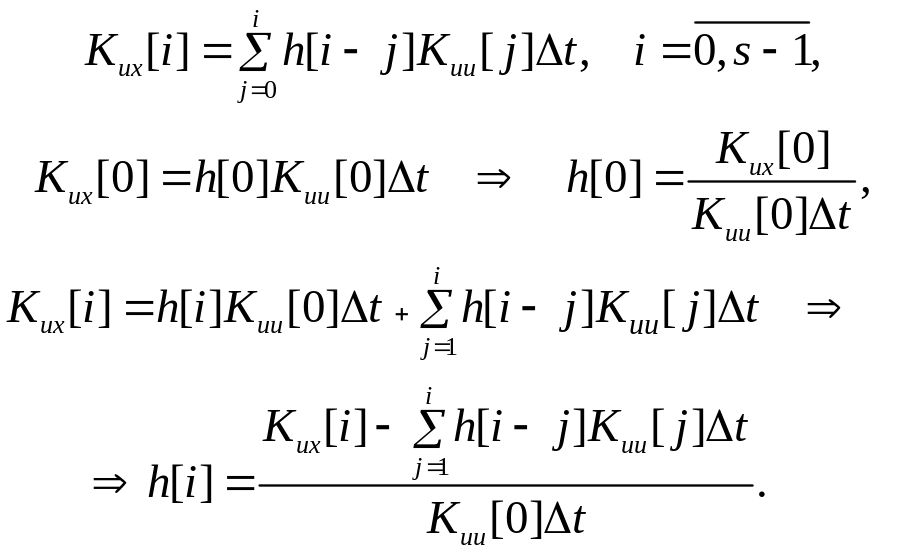 (4.39)
(4.39)
Полученную выборку весовой функции будем рассматривать как регрессию. Оценка весовой функции выглядит следующим образом:
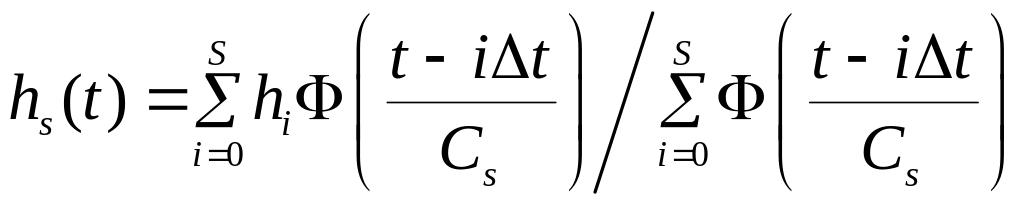 ,
(4.40)
,
(4.40)
где колоколообразные
функции
![]() и параметр размытости
и параметр размытости
![]() должны
удовлетворять некоторым условиям
сходимости.
должны
удовлетворять некоторым условиям
сходимости.
Весовая функция линейной динамической системы является определяющей ее характеристикой. Поэтому, подставив данную оценку весовой функции в интеграл Дюамеля, получим модель ЛДС:
![]() . (4.41)
. (4.41)
Таким образом, была построена модель ЛДС при произвольном входном сигнале в условиях непараметрической неопределенности.
Существуют различные способы оценивания импульсной переходной функции системы. Один из таких способов – это идентификация с использованием корреляционных методов теории случайных процессов. Опишем одну из разновидностей корреляционного метода идентификации. Введем автокорреляционную функцию входа
![]() (4.42)
(4.42)
и взаимную корреляционную функцию входа и выхода
![]() ,
(4.43)
,
(4.43)
где
![]() – случайная функция входа линейной
системы;
– случайная функция входа линейной
системы;
![]() – выход ЛДС,
– выход ЛДС,
![]() ;
;
![]() – соответственно математические
ожидания входного и выходного процессов;
T –
время, в течение которого измеряются
входной и выходной процессы.
– соответственно математические
ожидания входного и выходного процессов;
T –
время, в течение которого измеряются
входной и выходной процессы.
Ввиду того что время T на практике всегда ограничено, вместо корреляционных функций используют их оценки:
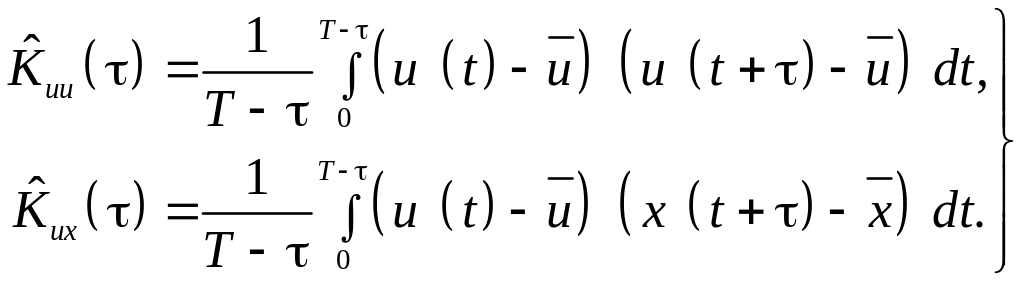 (4.44)
(4.44)
Уравнением идентификации линейной стохастической динамической стационарной системы является уравнение Винера–Хопфа при нулевых начальных условиях:
![]() .
(4.45)
.
(4.45)
Идентификация в этом случае сводится к определению импульсной переходной функции , т. е. к решению интегрального уравнения (4.45).
В частности,
существует способ оценки
,
когда входной сигнал является практически
белым, при этом автокорреляционная
функция
![]() имеет дельтообразный характер:
имеет дельтообразный характер:
![]() (4.46)
(4.46)
Тогда из (4.45) получаем:
 .
(4.47)
.
(4.47)
При этом взаимная
корреляционная функция оказывается
хорошим приближением для весовой функции
исследуемого объекта. Добавим к входу
объекта белый шум
![]() так, что
так, что
![]() ,
(4.48)
,
(4.48)
где n(t)
– белый шум, автокорреляционная функция
которого является
δ-функцией
![]() .
.
Подставим
![]() в уравнение (4.45):
в уравнение (4.45):
 .
(4.49)
.
(4.49)
Следовательно,
![]() (4.50)
(4.50)
т. е. добавляя к
регулярному входу объекта пробный
случайный сигнал в виде белого шума, мы
получаем импульсную переходную функцию
как корреляционную функцию этого сигнала
и выхода объекта, умноженную на мощность
сигнала:
![]()
Метод оценивания импульсной переходной функции, основанный на изложенном выше принципе, имеет три основных преимущества:
– для идентификации системы не требуется обязательной регистрации ее функционирования в условиях нормальной эксплуатации;
– определение корреляционных характеристик для достаточно длинных промежутков времени позволяет выбирать очень небольшую амплитуду тестового сигнала;
– не требуется дополнительной априорной информации о структуре идентифицируемой системы.
Однако этот метод имеет и ряд недостатков, которые ограничивают его применение:
– для получения точных оценок взаимной корреляционной функции нужны продолжительные наблюдения;
– потребность в источнике белого шума обусловливает необходимость в дополнительном техническом и программном обеспечении.
Практическая
реализация белого шума как случайного
процесса с дельтообразной автокорреляционной
функцией невозможна, и поэтому обычно
используют квазибелый шум в виде
двоичного случайного процесса, который
через равные промежутки времени
![]() принимает равновероятно одно из двух
значений ±a.
Автокорреляционная функция такого
случайного процесса имеет следующий
вид:
принимает равновероятно одно из двух
значений ±a.
Автокорреляционная функция такого
случайного процесса имеет следующий
вид:
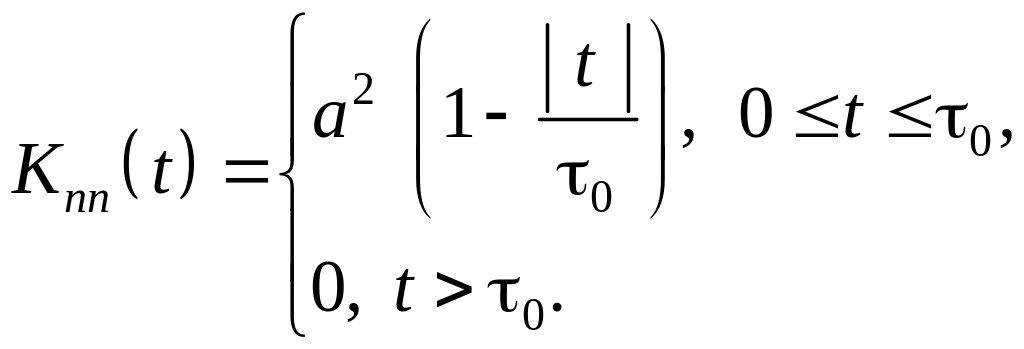 (4.51)
(4.51)
При малом значении параметра эта зависимость хорошо аппроксимирует δ-функцию (рис. 4.7). Тогда в (4.39) все члены суммы станут равными нулю и формула для вычисления весовой функции примет вид
![]() .
(4.52)
.
(4.52)
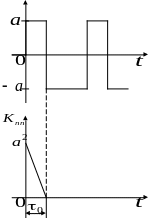
Рис. 4.7. Квазибелый шум и его корреляционная функция
Подставив данную оценку весовой функции в интеграл Дюамеля (4.41), получим модель ЛДС.
Таким образом, мы рассмотрели задачи идентификации ЛДС в условиях непараметрической неопределенности. Одна из этих задач посвящена построению непараметрической модели при произвольном входном сигнале, другая – случаю подачи на вход исследуемого объекта сигналов специального вида.
