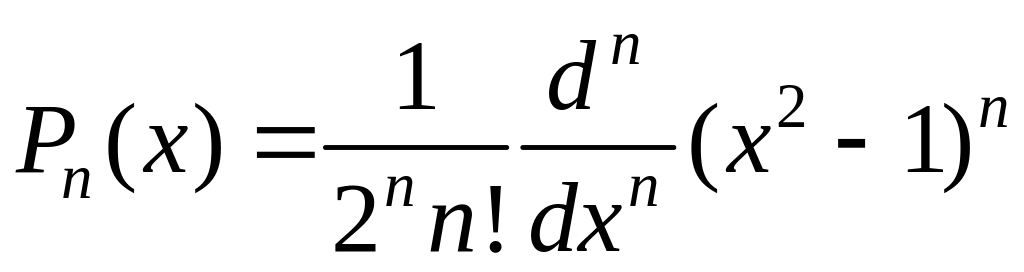1.3. Идентификация линейных по параметрам моделей с использованием метода наименьших квадратов

Рассмотрим задачу оценивания функциональной зависимости по выборке некоррелированных и равноточных измерений этих переменных , в случае, когда уравнение этой зависимости представляет собой функцию, линейную относительно параметров:

.

(1.16)

В матричной форме это уравнение имеет вид

,

(1.17)

где 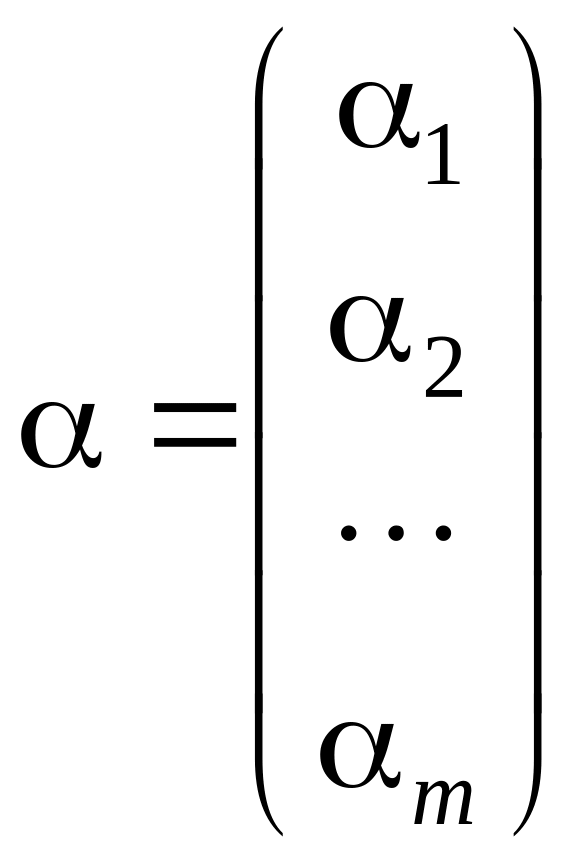– вектор параметров модели; 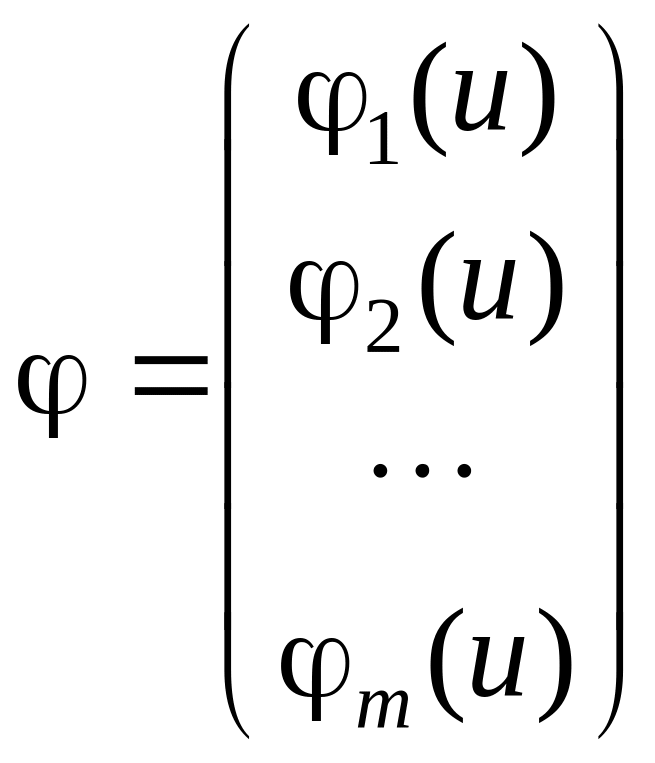– вектор базисных функций.

Также введем следующие матрицы:

– матрицу, составленную из базисных функций, рассчитанных в выборочных значениях независимой переменной:

;

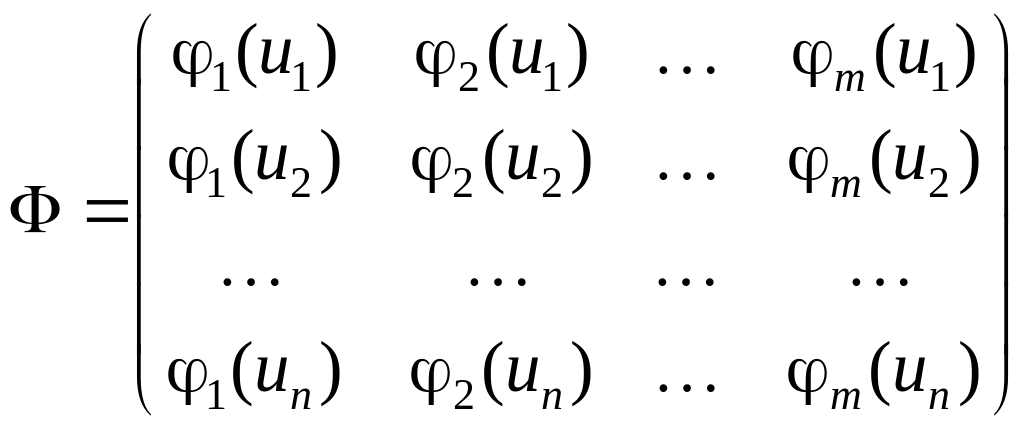– вектор выборочных значений зависимой переменной:

.

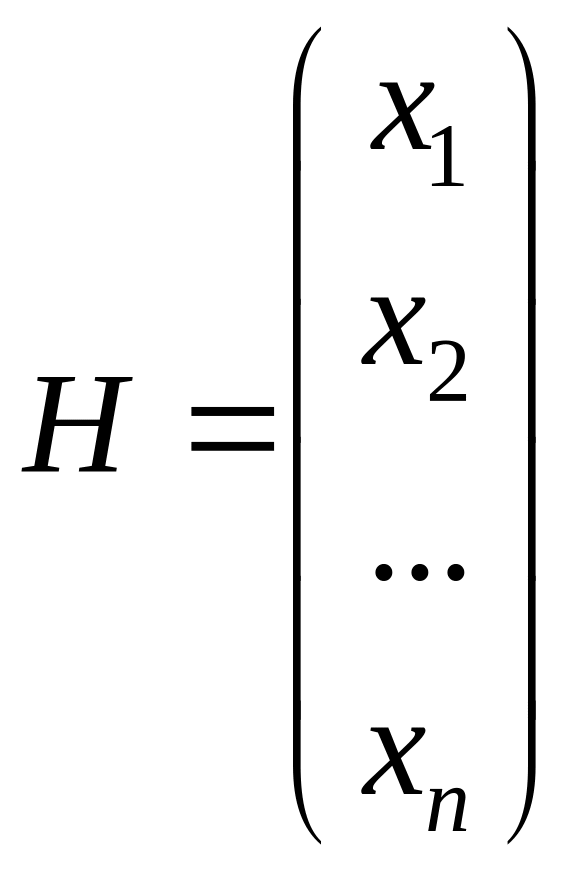Подставляя в уравнение (1.17) поочередно все элементы выборки, получим несовместную систему уравнений:

.

(1.18)

Выполним преобразование, умножив левую и правую части уравнения на :

.

(1.19)

В литературе это уравнение носит название нормального уравнения. Покажем, что это уравнение тождественно необходимому условию минимума критерия МНК: .

Пусть уравнение регрессии принимается в виде линейной функции первого порядка:

.

Оптимизация критерия МНК приводит к необходимости решения системы уравнений:

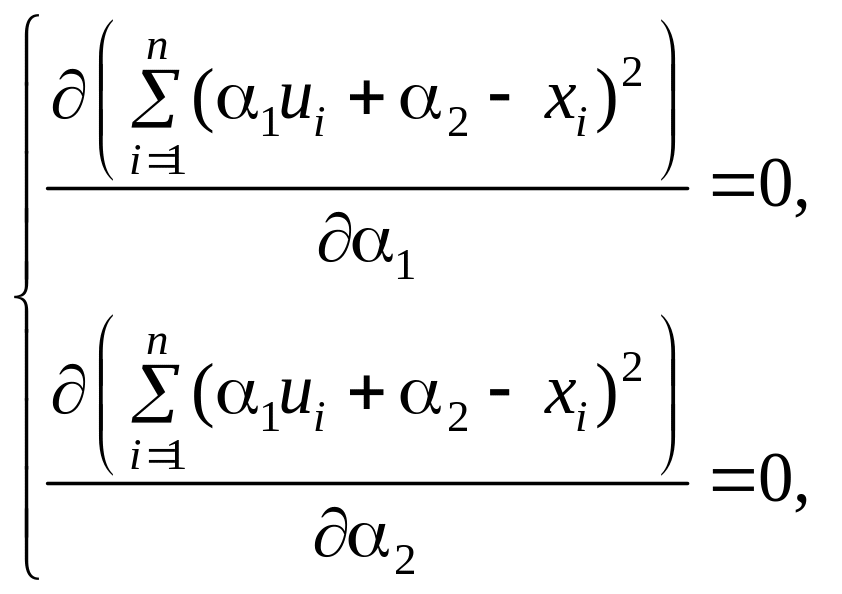
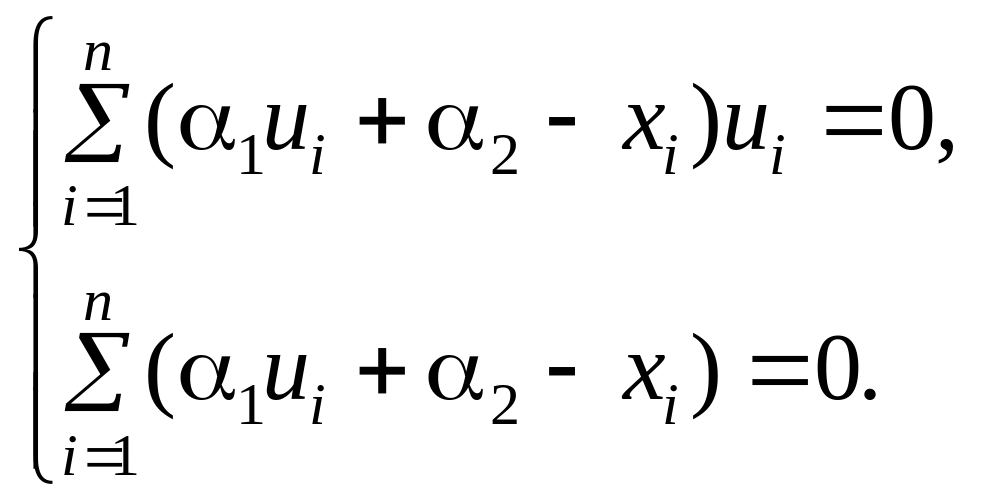
Эта система идентична уравнению (1.19) со следующими параметрами:

, , , .

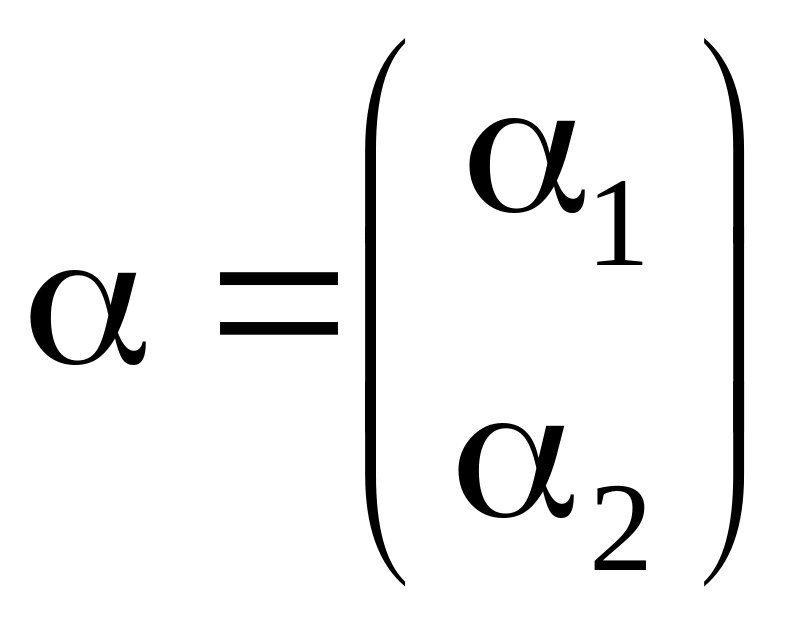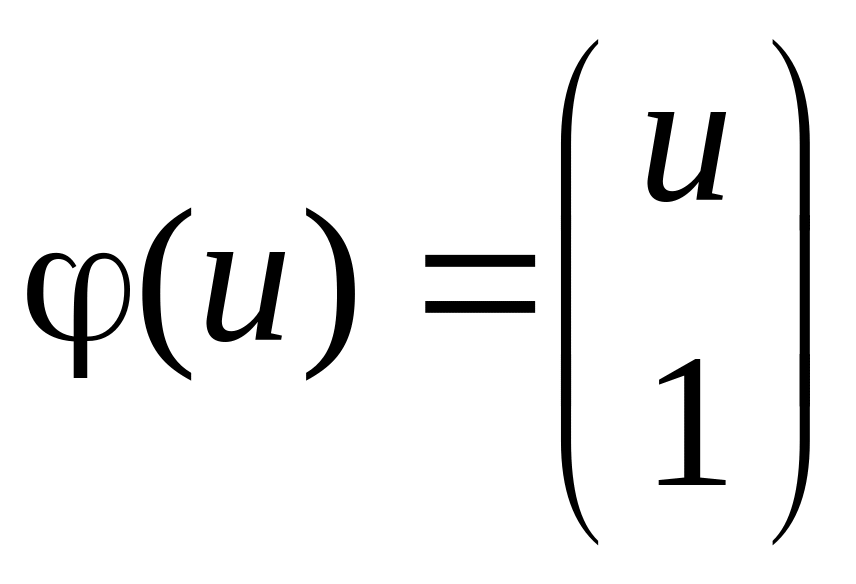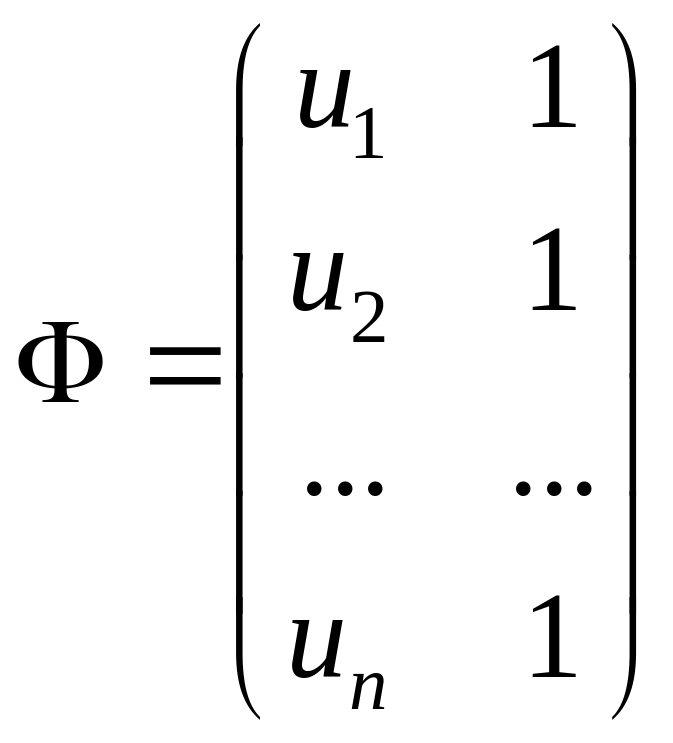Вектор параметров модели является решением нормального уравнения (1.19):

.

(1.20)

Для линейной модели с двумя параметрами получаем

.

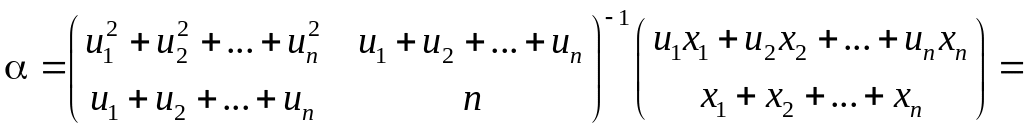
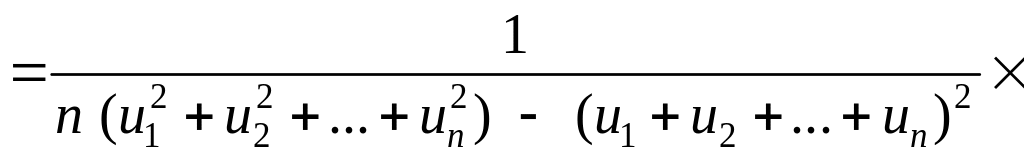
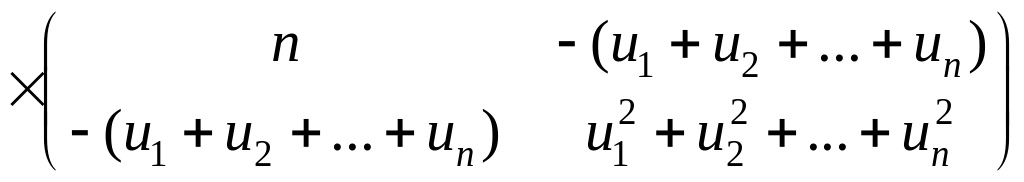
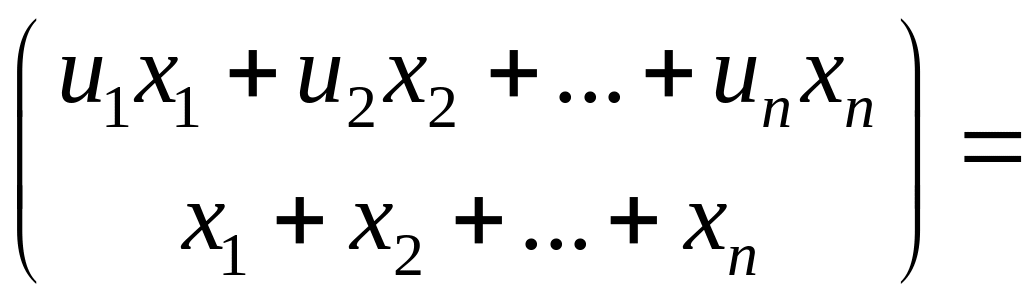
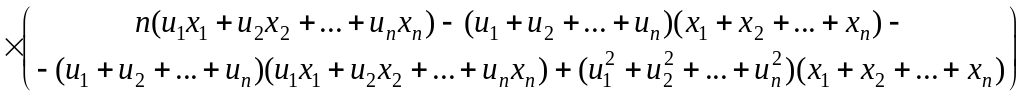Аналогично происходит вывод вектора α бóльших размерностей.

1.4. Линейный метод наименьших квадратов с использованием ортогональных полиномов

Теория ортогональных полиномов – одна из ветвей математического анализа. Ее первые результаты были получены в конце XVIII – начале XIX в., но интенсивно эта теория начала развиваться с середины XIX в. Огромный вклад в становление и развитие этой теории внесли и российские математики.

Непрерывные функции и ортогональны с весом на интервале , если справедливо равенство

.

Введем понятие ортогональности для вектора базисных функций в дискретном случае. Пусть вектор базисных функций  таков, что входящие в него функции попарно ортогональны для заданной выборки, т. е. для любой пары , выполняется условие

.

(1.21)

В этом случае матрица превращается в диагональную, а значит, система уравнений (1.19) распадается на m независимых уравнений:

(1.22)

Независимость этих уравнений приводит к тому, что оценки коэффициентов при базисных функциях не зависят от значений других базисных функций. Кроме того, если часть использующихся базисных функций отбросить, то оценки коэффициентов при оставшихся функциях не изменятся.

Приведем примеры ортогональных полиномов.

Полиномы Чебышёва. П. Л. Чебышёв (1821–1894) – знаменитый русский математик, создатель Санкт-Петербургской математической школы. В статистике его имя известно главным образом по так называемому неравенству Чебышёва, которое он предложил для распределения вероятностей и которое имеет силу для любого статистического распределения. Однако в последнее время в статистике все большее значение приобретают ортогональные полиномы Чебышёва, предложенные им в 1855 г. Эти полиномы используются при определении множественной и криволинейной регрессии и при вычислении коэффициентов обобщенной функции нормального распределения вероятностей.

Полиномы Чебышёва первого рода T_n(x) (рис. 1.2) и второго рода U_n(x) ортогональны на интервале с весовыми функциями и соответственно и определяются как

Tn(x) = cos(n arccos x), Un(x) = sin((n +1) arccos x) / sin(arccos x).

(1.23)

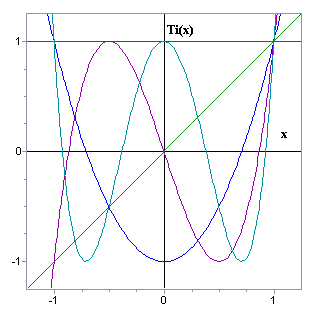
Рис. 1.2. Полиномы Чебышёва первого рода

Они также могут быть получены при помощи рекуррентного отношения:

T0(x) = 1, T1(x) = x, Tn+1(x) = 2xTn(x) – Tn–1(x),

(1.24)

U0(x) = 1, U1(x) = 2x, Un+1(x) = 2xUn(x) – Un–1(x).

(1.25)

Полиномы Эрмита. Полиномы Эрмита H_n(x) (рис. 1.3) ортогональны на интервале (–; ) с весовой функцией Они определяются по выражению

(1.26)

или могут быть получены при помощи рекуррентной формулы:

H0(x) = 1, H1(x) = 2x, Hn+1(x) = 2xHn(x) – 2nHn–1(x).

(1.27)

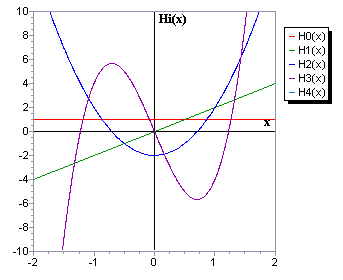
Рис. 1.3. Полиномы Эрмита

Полиномы Лагерра. Полиномы Лагерра L_n(x) (рис. 1.4) ортогональны на интервале [0; ) с весовой функцией и определяются как решения дифференциального уравнения Лагерра:

xy'' + (1 – x)y' + ny = 0.

(1.28)

L_i(x)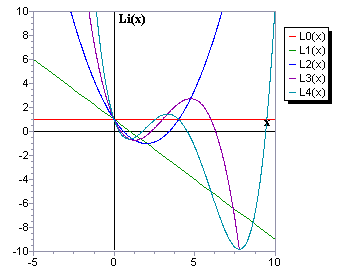

Рис. 1.4. Полиномы Лагерра

Решения, соответствующие целым неотрицательным значениям n, могут быть получены при помощи формулы Родрига (Родригеса):

(1.29)

или рекуррентной формулы

L0(x) = 1, L1(x) = 1 – x, (n + 1)Ln+1 (x) = (2n + 1 – x)Ln (x) – nLn–1 (x).

(1.30)

Полиномы Лежандра. Полиномы Лежандра P_n(x) (рис. 1.5), иногда называемые функциями Лежандра первого рода, ортогональны на интервале с весовой функцией и определяются как решения дифференциального уравнения Лежандра:

.

(1.31)

Решения, соответствующие целым неотрицательным значениям n, могут быть получены при помощи формулы Родрига (Родригеса):

(1.32)

или при помощи рекуррентной формулы:

P0(x) = 1, P1(x) = x, (n + 1)Pn+1(x) = (2n + 1) xPn(x) – nPn–1(x).

(1.33)

Р_i(x)

x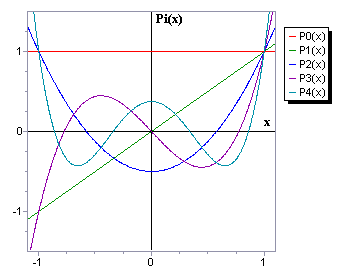

Рис. 1.5. Полиномы Лежандра

Другие разновидности ортогональных полиномов можно найти в специальной и справочной литературе¹.
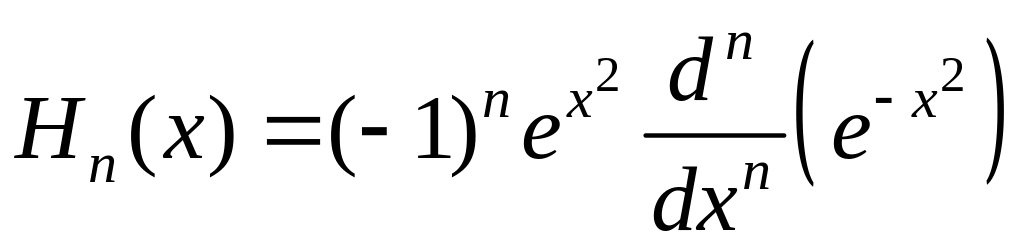
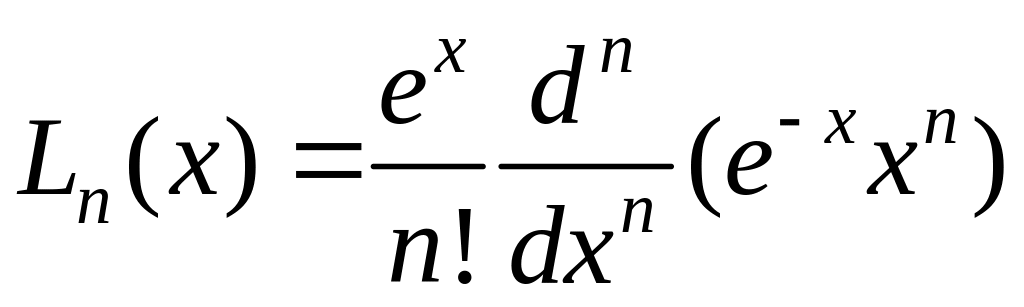
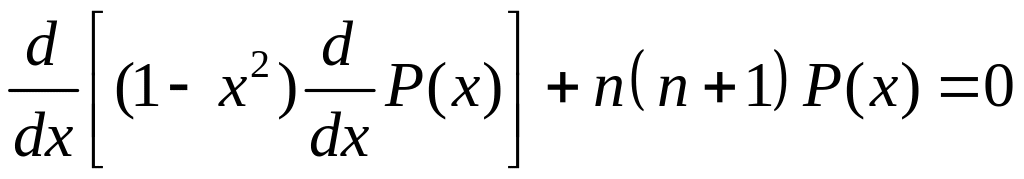